Момент инерции твердого тела. Теорема Штейнера. Основное уравнение вращательного движения. Ускорение центра масс полого цилиндра, скатывающегося с наклонной плоскости.
Момент инерции твердого тела.
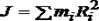- является моментом инерции тела относительно оси вращения. (посмотреть вывод)
теорема Штейнера: момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями
J=J0+md2.
Ускорение центра масса полого цилиндра
Ускорение центра масс (по теореме о движении центра масс) определяется суммой внешних по отношению к системе сил, если считать их приложенными к некоторой эквивалентной материальной точке, которая помещена в центр масс и имеет массу.
(посмотреть вывод в допах или лекциях «Движение твердого тела»)
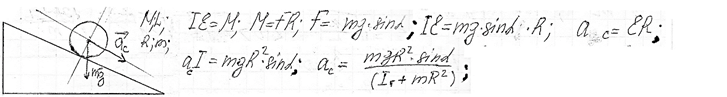
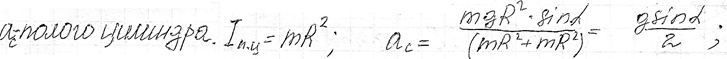
12. Момент инерции твердого тела. Теорема Штейнера. Основное уравнение динамики вращательного движения. Ускорение центра масс сплошного цилиндра, скатывающегося с наклонной плоскости.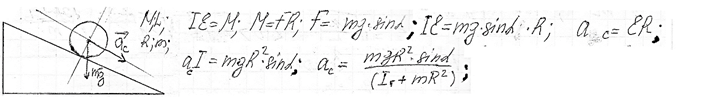 
13. Момент инерции твердого тела. Теорема Штейнера. Основное уравнение динамики вращательного движения. Ускорение центра масс шара, скатывающегося с наклонной плоскости.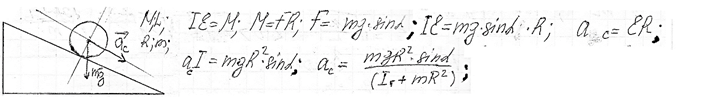
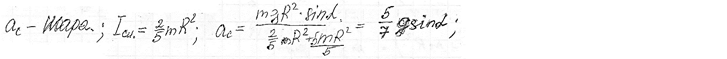
Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина однородного стержня, качающегося в поле силы тяжести.
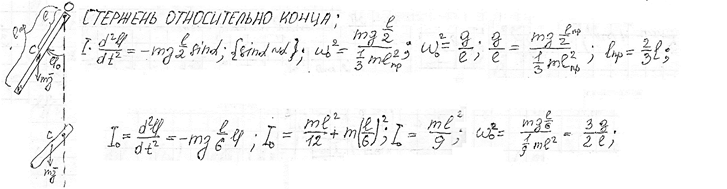
Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина тонкого кольца, качающегося в поле силы тяжести.
|
|
|
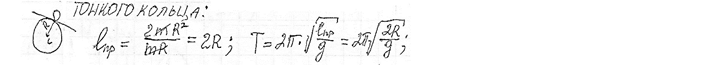
Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина сплошного диска, качающегося в поле силы тяжести.
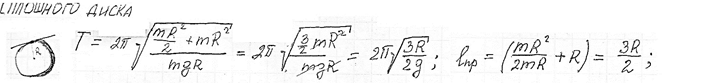
Физический маятник. Уравнение движения физического маятника. Приведенная длина физического маятника. Период колебаний и приведенная длина однородного шара, качающегося в поле силы тяжести.
17.1. Физический маятник – твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. При отклонении маятника на α (рис. 7.4) возникает вращательный момент, стремящийся вернуть маятник в положение равновесия: 
расстояние между точкой подвеса О и центром масс С. Знак «– » ставиться потому что при отклонении маятника возникает вращательный момент который пытается вернуть его в положение равновесия и аналогичен в этом случае квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению нужно приписать противоположные знаки.
|
|
|
17.2. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать уравнение динамики вращательного движения: 
при малых колебаниях уравнение имеет вид: 
Из данных уравнений следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, чатсота которых зависит от массы, момента инерции относительно оси вращения и расстоянию между оси вращения и центром масс маятника. В соответствии с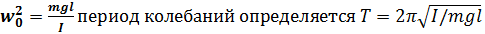 
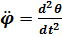17.3. Из сопоставления формул периода колебаний математического 
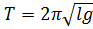и физического маятника 
получается что математический маятник длинной 
будет иметь период колебаний как и физический маятник. Данную величину называют приведенной длинной физического маятника – это длина такого математического маятника, период колебания которого совпадает с периодом данного физического маятника. Центр качения физического маятника (точка 
– точка на прямой соединяющая точку подвеса с центром масс, лежащая на расстоянии приведенной длинны от оси вращения.
|
|
|
При подвешивания маятника в центре качения период и приведенная длинна сохраняется, а значит точка подвеса и центр качения обладают свойством взаимности (при переносе точки подвеса в центр качения прежняя точка становиться новым центром качения) 17.4.
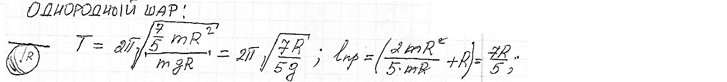
Волновые процессы. Продольные и поперечные волны. Уравнение плоской волны. Период и частота колебаний волнового процесса. Длина волны и волновое число. Волновое уравнение. Фазовая скорость.
Дата добавления: 2018-11-24; просмотров: 1503; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!