Состояние механической системы. Законы Ньютона. Уравнения движения и начальные у Движение тела, брошенного под углом к горизонту. Максимальная высота подъема и дальность полета.
1.1. Состоянием механической системы назовется значение положения этой системы (координаты ( x : y : z)) и импульса этой системы. 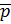 Принцип детерминированности Ньютона утверждает, что состояние механической системы, заданное в любой момент времени, однозначно определяет все ее дальнейшее движение. Рассмотрим изолированную систему двух материальных точек в инерциальной системе отчета с координатами состояния
Принцип детерминированности Ньютона утверждает, что состояние механической системы, заданное в любой момент времени, однозначно определяет все ее дальнейшее движение. Рассмотрим изолированную систему двух материальных точек в инерциальной системе отчета с координатами состояния  Когда эти точки взаимодействуют, то изменение скоростей этих точек не будет одинаковым. Вместе с тем, материальной точке можно сопоставить такую скалярную постоянную
Когда эти точки взаимодействуют, то изменение скоростей этих точек не будет одинаковым. Вместе с тем, материальной точке можно сопоставить такую скалярную постоянную 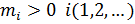 называемую массой, что будет выполнено равенство:
называемую массой, что будет выполнено равенство: 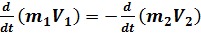 Аксиома: Масса материальной точки сохраняет свое значение не только по времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий.
Аксиома: Масса материальной точки сохраняет свое значение не только по времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий.
Законы Ньютона
Законы Ньютона — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел.
Первый закон Ньютона формулируется следующим образом: всякое тело, находящееся в состоянии покоя или равномерного и прямолинейного движения , пока воздействие со стороны других тел не заставит его изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Первый закон Ньютона выполняется не во всякой системе отчета. А система отчета, в которой выполняется первый закон Ньютона, называется инерциальной (система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно либо покоятся). Система отчета, в которой 1–й З.Н. не выполняется, называется не инерциальной системой отчета.
Второй закон Ньютона гласит, что скорость изменения импульса тела равна действующей на тело сите F : 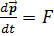 данное уравнение называется уравнением движения тела. Заменив p импульс согласно
данное уравнение называется уравнением движения тела. Заменив p импульс согласно 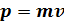 и учтя, что в Ньютоновсой механике масса предполагается постоянной, можно представить данное уравнение в виде
и учтя, что в Ньютоновсой механике масса предполагается постоянной, можно представить данное уравнение в виде 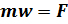 где w = v w – ускорение. Таким образом, мы пришли к другой формулировке второго закона Ньютона.: произведение массы тела, на его ускорение равно действующей на тело силе. Второй закон Ньютона справедлив только в инерциальных системах отсчета.
где w = v w – ускорение. Таким образом, мы пришли к другой формулировке второго закона Ньютона.: произведение массы тела, на его ускорение равно действующей на тело силе. Второй закон Ньютона справедлив только в инерциальных системах отсчета.
При независимом выборе единиц массы, силы и ускорения выражение второго закона Ньютона нужно записать в виде: 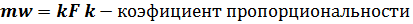 Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, все гда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, все гда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки: 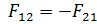 . где
. где 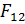 — сила, действующая на первую материальную точку со стороны второй;
— сила, действующая на первую материальную точку со стороны второй; 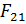 — сила, действующая на вторую материальную точку со стороны первой. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками. Третий закон Ньютона, как впрочем и первые два, справедлив только в инерциальных системах отсчета.
— сила, действующая на вторую материальную точку со стороны первой. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками. Третий закон Ньютона, как впрочем и первые два, справедлив только в инерциальных системах отсчета.
1.3.  Уравнения движения и начальные условия. Уравнение движения (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или динамической системы (например, поля) во времени и пространстве. Эволюция физической системы однозначно определяется уравнениями движения и начальными условиями. Уравнение движения записывается в виде
Уравнения движения и начальные условия. Уравнение движения (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или динамической системы (например, поля) во времени и пространстве. Эволюция физической системы однозначно определяется уравнениями движения и начальными условиями. Уравнение движения записывается в виде 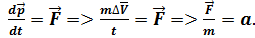 Под начальными условиями понимают начальный импульс
Под начальными условиями понимают начальный импульс  и
и 
1.4. и 1.5. Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения ; проекции ускорения на координатные оси равны 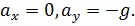 Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y). Проекции скорости тела, следовательно, изменяются со временем следующим образом:
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y). Проекции скорости тела, следовательно, изменяются со временем следующим образом: 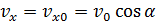
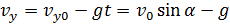 , где
, где 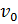 – начальная скорость,
– начальная скорость, 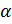 – угол бросания. Координаты тела, следовательно, изменяются так:
– угол бросания. Координаты тела, следовательно, изменяются так: 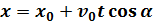
 При нашем выборе начала координат начальные координаты
При нашем выборе начала координат начальные координаты 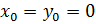 Тогда
Тогда 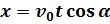
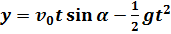 Проанализируем формулы
Проанализируем формулы 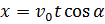
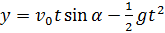 . Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
. Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета: 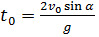 Дальность полета получим из первой формулы
Дальность полета получим из первой формулы 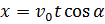
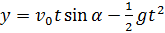 . Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение
. Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение  в первую формулу
в первую формулу 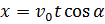
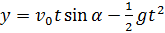 , получаем:
, получаем: 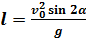 Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы 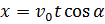
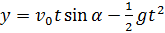 . Для этого нужно подставить в эту формулу значение времени, равное половине времени полета
. Для этого нужно подставить в эту формулу значение времени, равное половине времени полета  , т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
, т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем 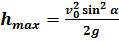 Из уравнений
Из уравнений 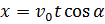
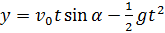 можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения
можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения 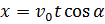
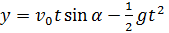 выразить время:
выразить время: 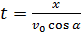 и подставить его во второе уравнение. Тогда получим:
и подставить его во второе уравнение. Тогда получим: 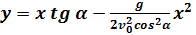 . Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
. Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
Дата добавления: 2018-11-24; просмотров: 313; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
