Распределение Максвелла. Средние тепловые скорости газовых молекул. Средняя длина свободного пробега молекул газа. Основное уравнение молекулярно-кинетической теории.
Распределение Максвелла. Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию.
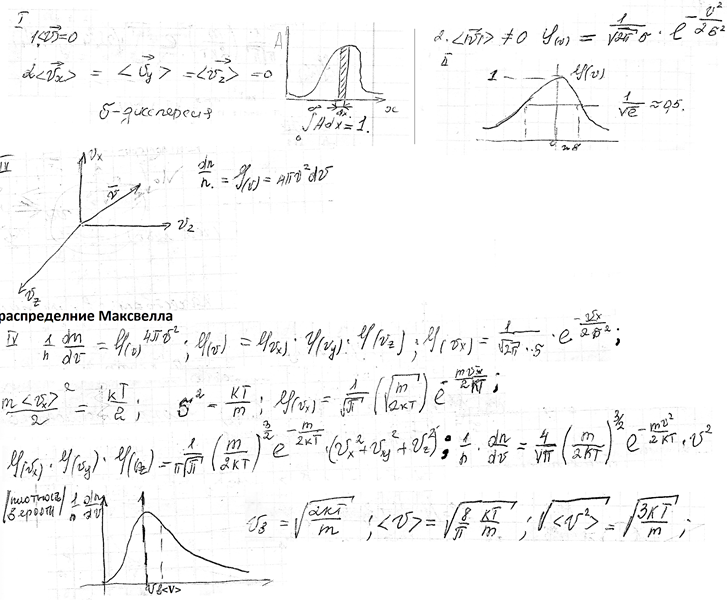
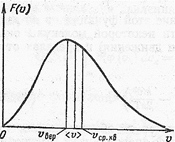
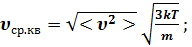
Средние тепловые скорости газовых молекул.
Bыведем среднюю скорость молекул. Вывод формулы начинается с закона изменения функции распределения молекул по скоростям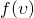 
:
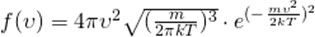
Что бы у нас получилась формула средней скорости молекул, надо взять интеграл этой функции от 0 до бесконечности:
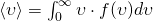
После взятия интеграла, у нас получается нужный нам результат — средняя скорость молекулы: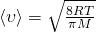 
А если расписать универсальную газовую постоянную, как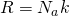 
, и за одно молярную массу 
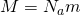, то у нас получится: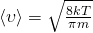 
Средняя длинна свободного пробега молекул газа. Под средней длиной свободного пробега понимают среднее расстояние, которое проходит молекула между двумя последовательными соударениями. За секунду молекула в среднем проходит расстояние, численно равное ее средней скорости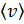 
. Если за это же время она испытает в среднем 
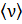столкновений с другими молекулами, то ее средняя длина свободного пробега 
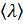, очевидно, будет равна 
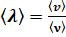. Если в единице объема газа находится 
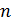молекул, то число столкновений рассматриваемой молекулы за одну секунду будет равно: 
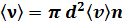(Молекула столкнется со всеми неподвижными молекулами, центры которых находятся в пределах ломаного цилиндра диаметром 2d. За секунду молекула проходит путь, равный 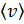. Поэтому число происходящих за это время столкновений равно числу молекул, центры которых попадают внутрь ломаного цилиндра, имеющего суммарную длину 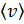. и радиус 
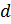. Его объем примем равным объему соответствующего спрямленного цилиндра, т. е. равным 
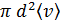). Как показывают соответствующий расчет, средная скорость относительно движения молекул 
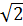раз больше скорости 
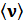молекул относительно стенок сосуда. Поэтому среднее число столкновений в секунду равно: 
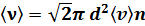. С учетом последнего выражения формула для средней длины свободного пробега приобретает вид: 
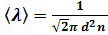. Заменив эквивалентный диаметр 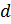эффективным сечением 
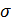, получим следующую формулу: 
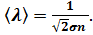Так как при постоянной температуре 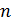изменяется пропорционально давлению 
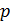, средняя длинна свободного пробега обратно пропорциональна давлению: 
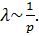Эффективный диаметр молекул, как уже отмечалось, убывает с ростом температуры. Поэтому средняя длинна свободного пробега с повышением температуры растет.
|
|
|
Основное уравнение МКТ. Уравнения вида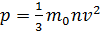 
Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения). А так же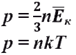 
Дата добавления: 2018-11-24; просмотров: 408; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!