ЭНТРОПИЯ И ПРИВЕДЕННАЯ ТЕПЛОТА. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ И НАПРАВЛЕНИЕ ПРОЦЕССА. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ. ИДЕАЛЬНАЯ ТЕПЛОВАЯ МАШИНА И ВОЗРАСТАНИЕ ЭНТРОПИИ.
Энтропия – функция состояния системы, изменение которой равно отношению бесконечно малого количества теплоты, введенного в этом процессе, к температуре при которой оно вводилось: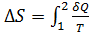 
. Изменение энтропии за цикл Карно равно нулю, так как система возвращается в исходное состояние, еще нельзя не учесть то, что при адиабатических процессах изменение энтропия постоянна, а на участках 1-2 и 3-4 изменение энтропии равно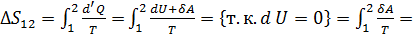 
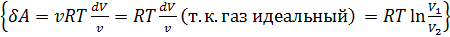
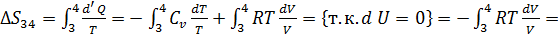
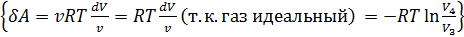
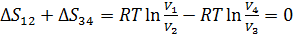Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно 
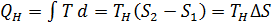.Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику 
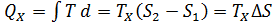. Отсюда коэффициент полезного действия тепловой машины Карно равен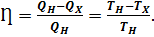 
Энтропия и приведенная теплота.
Из рассмотренного цикла Карно (п. 5.4) видно, что равны между собой отношения теплот к температурам, при которых они были получены или отданы в изотермическом процессе: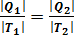 
Отношение теплоты 
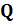в изотермическом процессе к температуре, при которой происходила передача теплоты, называется приведенной теплотой 
: 
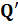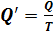Для подсчета приведенной теплоты в произвольном процессе необходимо разбить этот процесс на бесконечно малые участки, где Т можно считать константой. Приведенная теплота на таком участке будет равна 
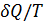Суммируя приведенную теплоту на всех участках процесса, получим: 
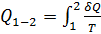Тогда в обратимом цикле Карно (п. 5.3, 5.4) имеем: 
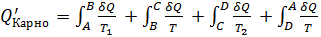Этот результат справедлив для любого обратимого процесса. Таким образом, для процесса, происходящего по замкнутому циклу 
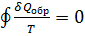Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подынтегральное выражение 
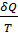есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Это позволяет ввести новую функцию состояния S: 
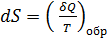Функция состояния, полный дифференциал которой равен 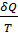, называется энтропией (от греч. entropia – поворот, превращение) – мера способности теплоты превращаться в другие виды энергии.
Энтропия S – это отношение полученной или отданной теплоты к температуре, при которой происходил этот процесс. Для обратимых процессов изменение энтропии, как следует из 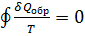, 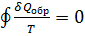Это выражение называется равенство Клаузиуса.
|
|
|
|
|
|
Для суждения о возможном направлении процессов в термодинамике вводится еще одна функция состояния – энтропия. Так как энтропия является функцией состояния макросистемы, то внутренняя энергия может рассматриваться как функция энтропии и, в простейшем случае, одного внешнего параметра, например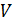 
. Тогда 
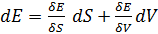. При равновесных процессах 
.
|
|
|
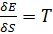Второе начало термодинамики и направление процесса Появление второго начала термодинамики прежде всего связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие нет. Второе начало термодинамики задает направление протекания термодинамических процессов.
Используя понятие энтропии и связанное с ним неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.
Можно дать более короткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Существенен момент, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя произвольным образом (возрастать, убывать, оставаться постоянной). Кроме того, повторим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах и в замкнутой системе энтропия всегда возрастает.
Формула Больцмана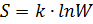 
дает объяснение постулируемое вторым началом термодинамики возрастанию энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Значит, формула Больцмана дает статистическое толкование второго начала термодинамики. Являясь статистическим законом, оно описывает закономерности хаотического движения огромного числа частиц, которые составляющих замкнутую систему.
Дадим еще две формулировки второго начала термодинамики:
1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;
2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.
Можно довольно просто доказать эквивалентность формулировок Кельвина и Клаузиуса. Более того, показано, что если в замкнутой системе провести воображаемый процесс, который противоречит второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это же доказывает эквивалентность формулировки Клаузиуса (а значит, и Кельвина) и статистической формулировки, по которой энтропия замкнутой системы не может убывать. Закон возрастания энтропии. Если замкнутая система не находится в состоянии статистического равновесия, то с течением времени ее макроскопическое состояние будет изменяться, пока система в конце концов не придет в состояние полного равновесия. Характеризуя каждое макроскопическое состояние системы распределением энергии между различными подсистемами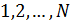 
мы можем сказать, что ряд последовательно проходимых системой состояний соответствует все более вероятному распределению энергии. Это возрастание вероятности, вообще говоря, чрезвычайно значительно в силу его экспоненциального характера. Мы видели, что вероятность определяется выражением 
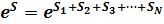в экспоненте, которого стоит аддитивная величина – энтропия системы. Мы можем поэтому сказать, что процессы, протекающие в неравновесной замкнутой системе, идут таким образом, что система непрерывно переходит из состояний с меньшей в состояния с большей энтропией, пока, наконец, энтропия не достигнет наибольшего возможного значения, соответствующего полному статистическому равновесию. Таким образом, если замкнутая система в некоторый момент времени находится в неравновесном макроскопическом состоянии, то наиболее вероятным следствием в последующие моменты времени будет монотонное возрастание энтропии системы. Это есть так называемый закон возрастания энтропии, или второй закон термодинамики.
|
|
|
Идеальная тепловая машина и возрастание энтропии.
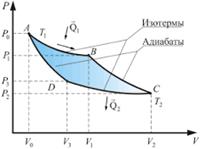
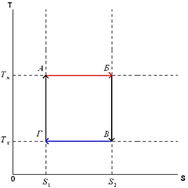Идеальная тепловая машина — машина в которой произведенная работа и разница между количеством подведенного и отведенного тепла равны. Работа идеальной машины описывается циклом Карно.Изменение энтропии за цикл равно 0, а возрастание энтропии происходит на участках изотермических процессов. Изменение энтропии за этот цикл равно: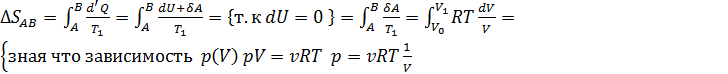 
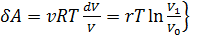
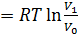
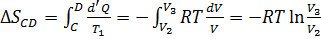
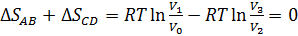1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру 
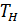, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты 
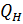. При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает. 2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника 
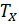, тело совершает механическую работу, а энтропия остаётся постоянной. 3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру 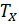, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты 
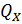. Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Дата добавления: 2018-11-24; просмотров: 1431; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!