Теплоемкость политропных процессов
Nbsp; МИНОБРНАУКИ РОССИИ Государственное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)» (СПбГЭТУ «ЛЭТИ»)
МЕХАНИКА
ТЕРМОДИНАМИКА
Механика. Термодинамика: Методические указания по подготовке студентов к экзамену.
Содержат основные формулы и теоретический материал по курсу «Общая физика» (разделы «Механика» и «Термодинамика»).
Предназначены для студентов 1-го курса всех технических факультетов.
Санкт-Петербург
2016
Вопросы к экзамену ФРТ 1 семестр, 2015
Основы молекулярно-кинетическом теории и термодинамики
ДИНАМИЧЕСКИЙ, ТЕРМОДИНАМИЧЕСКИЙ И СТАТИСТИЧЕСКИЙ МЕТОДЫ ОПИСАНИЯ МАКРОСИСТЕМ. ПАРАМЕТРЫ И ПИИ СОСТОЯНИЯ. МИКРО И МАКРОСОСТОЯНИЯ. ВЕРОЯТНОСТЬ СОСТОЯНИЯ. ТЕРМОДИНАМИЧЕСКАЯ ВЕРОЯТНОСТЬ. ЭНТРОПИЯ В СТАТИСТИЧЕСКОЙ ФИЗИКЕ.
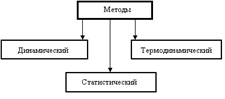 Динамический, термодинамический и статистический методы описания макросистем. Динамический метод предполагает использование законов классической механики для описания движения и взаимодействия каждой из N микрочастиц макросистемы. Мы упоминаем о динамическом методе описания макросистем, так как нет принципиальных возражений против такого подхода. Однако в этом случае придется записать и решить систему 6N уравнений движения и скоростей. Вспомним, что N ~ 1023 только в одном моле вещества. Система 6N уравнений становится необозримой по объему и недоступной для анализа. Эта «техническая» проблема не позволяет реально применить динамический метод для исследования макросистем. Статистический метод устанавливает связь между поведением макросистемы в целом с поведением и свойствами отдельных частиц, оперирует средними значениями механических параметров и опирается на законы теории вероятностей. В основе этого метода, лежит молекулярно кинетическая теория строения вещества. Термодинамический метод описывает только поведение макросистемы в целом, использует так называемые термодинамические параметры: температуру T, давление p, объем V и другие. При этом термодинамический метод базируется на общих принципах или началах, которые представляют собой обобщение многочисленных экспериментальных данных, в частности, на законе сохранения энергии. Фундаментом термодинамического метода являются два энергетических положения: Принцип эквивалентности теплоты и работы (I начало термодинамики) и теория тепловых машин Сади Карно (II начало термодинамики). Статистический и термодинамический методы взаимно дополняют друг друга. Параметры и функции состояния. Термодинамическая система характеризуется определенными значениями ее свойств. Эти свойства термодинамического тела (системы) называются параметрами состояния.
Динамический, термодинамический и статистический методы описания макросистем. Динамический метод предполагает использование законов классической механики для описания движения и взаимодействия каждой из N микрочастиц макросистемы. Мы упоминаем о динамическом методе описания макросистем, так как нет принципиальных возражений против такого подхода. Однако в этом случае придется записать и решить систему 6N уравнений движения и скоростей. Вспомним, что N ~ 1023 только в одном моле вещества. Система 6N уравнений становится необозримой по объему и недоступной для анализа. Эта «техническая» проблема не позволяет реально применить динамический метод для исследования макросистем. Статистический метод устанавливает связь между поведением макросистемы в целом с поведением и свойствами отдельных частиц, оперирует средними значениями механических параметров и опирается на законы теории вероятностей. В основе этого метода, лежит молекулярно кинетическая теория строения вещества. Термодинамический метод описывает только поведение макросистемы в целом, использует так называемые термодинамические параметры: температуру T, давление p, объем V и другие. При этом термодинамический метод базируется на общих принципах или началах, которые представляют собой обобщение многочисленных экспериментальных данных, в частности, на законе сохранения энергии. Фундаментом термодинамического метода являются два энергетических положения: Принцип эквивалентности теплоты и работы (I начало термодинамики) и теория тепловых машин Сади Карно (II начало термодинамики). Статистический и термодинамический методы взаимно дополняют друг друга. Параметры и функции состояния. Термодинамическая система характеризуется определенными значениями ее свойств. Эти свойства термодинамического тела (системы) называются параметрами состояния.
Параметры состояния – любая величина, присущая телу, изменение которой определяется только начальным и конечным состоянием тела и не зависит от характера процесса изменения его состояния, при переходе его из первого состояния во второе. Параметры можно разделить на две группы: Интенсивные – которые не зависят от количества вещества и при взаимодейтсвии тел выравниваются (температура, давление и т.п.); Экстенсивные – зависящие от количества вещества, следующие закону сложения или, как говорят математики, закону аддитивности (масса, обьем, внутренняя энергия и т.п.). Измерение экстенсивной величины производится сравнением ее с такой же по природе величиной, выбранной за единицу – эталон (метр, килограмм и т.п.). Измерение интенсивной величины основано на использовании объективной связи между изменениями этой интенсивной величины и какой-либо экстенсивной величины. Например, связь температуры и объема жидкости в термометре приводит к измерению температуры с помощью длины столбика жидкости в термометре. Некоторые экстенсивные величины приобретают свойства интенсивных, если их рассматривают применительно к единице массы данного вещества (удельные объем, энтальпия и т.п.).
Все термодинамические параметры введены человеком для удобства изучения окружающего мира. Однако не все параметры поддаются измерению приборами. Ряд параметров, не поддающихся измерению, человек ввел для удобства расчета термодинамических процессов. Эти параметры получаются расчетным путем и имеют в размерности величину работы (энергии) Дж или кал. Например, к ним относятся энтальпия и энтропия. Такие параметры получили название – энергетических или калорических параметров, или функций состояния. Параметры, которые возможно измерить приборами, называются термическими. Например, к этим параметрам относятся температура и давление. Функция состояния в термодинамике — функция независимых параметров, определяющих равновесное состояние термодинамической системы; не зависит от пути (характера процесса), следуя которому система пришла в рассматриваемое равновесное состояние (т.е. не зависит от предыстории системы); к функциям состояния относят, в частности, характеристические функции системы: внутренняя энергия; энтропия – функция состояния термодинамической системы, определяемая тем, что ее дифференциал (dS) при элементарном равновесном (обратимом) процессе равен отношению бесконечно малого количества теплоты (  Q), сообщенной системе, к температуре (T):
Q), сообщенной системе, к температуре (T):  ; энтальпия – функция состояния термодинамической системы, равная сумме внутренней энергии и произведения объема на давление:; и др.
; энтальпия – функция состояния термодинамической системы, равная сумме внутренней энергии и произведения объема на давление:; и др.
Термодинамическая работа и количество теплоты не являются функциями состояния, так как их значение определяется видом процесса, в результате которого система изменила своё состояние.
Макро – и микросостояния. Микросостояние — это состояние системы, определяемое одновременным заданием координат и импульсов всех составляющих систему частиц. Знание микросостояния в некоторый момент времени позволяет однозначно предсказать эволюцию системы во все последующие моменты. Макросостояние — это состояние системы, характеризуемое небольшим числом макроскопических параметров. Одно макросостояние может быть реализовано большим числом микросостояний за счет перестановки частиц, не меняющей наблюдаемого состояния. Статистическое описание больших систем существенно опирается на следующие постулаты.
1. Все разрешенные микросостояния равновероятны. 2. Термодинамически равновесным является то макросостояние, которое реализуется наибольшим числом микросостояний, т. е. является наиболее вероятным состоянием.
 Вероятность состояния. Термодинамическая вероятность. Число микросостояний, соответствующих какому-либо макросостоянию системы, называется термодинамической вероятностью (статистическим весом) этого макросостояния. Термодинамическую вероятность будем обозначать буквой W.
Вероятность состояния. Термодинамическая вероятность. Число микросостояний, соответствующих какому-либо макросостоянию системы, называется термодинамической вероятностью (статистическим весом) этого макросостояния. Термодинамическую вероятность будем обозначать буквой W.
Главное свойство термодинамической вероятности:  в самопроизвольных процессах.
в самопроизвольных процессах.
Термодинамическая вероятность – характеристика состояния. Термодинамическая вероятность любого макросостояния системы не зависит от предшествующих и будущих состояний. Изменение термодинамической вероятности при переходе от одного макросостояния к другому не зависит от пути перехода, а зависит только от начального и конечного макросостояний. При циклическом процессе термодинамическая вероятность возвращается к исходному значению. Энтропия в статистической физике. Согласно Больцману (1872), энтропия системы и термодинамическая вероятность связаны между собой следующим образом: 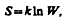
где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. РАБОТА И ВНУТРЕННЯЯ ЭНЕРГИЯ. ТЕПЛОЕМКОСТЬ ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС. ТЕПЛОЕМКОСТЬ И РАБОТА ИДЕАЛЬНОГО ГАЗА В ИЗОТЕРМИЧЕСКОМ ПРОЦЕССЕ.
Ое начало термодинамики
Представляет собой закон сохранения энергии для систем, в которых существенное значение имеют тепловые процессы. Количества теплоты, переданного системе равно сумме изменение внутренней энергии системы при переходе её из одного состояния в другое и работы внешних сил
Внутренняя энергия может изменяться в основном за счет двух процессов: совершения над телом работы  и сообщения ему количества теплоты
и сообщения ему количества теплоты  . Совершение работы сопровождается перемещением внешних тел, воздействующих на систему.
. Совершение работы сопровождается перемещением внешних тел, воздействующих на систему.
Расписав это уравнение относительно количества теплоты  Данное уравнение выражает закон сохранения энергии и представляет собой содержание первого начала термодинамики: Количество тепла, сообщенное системе, идет на приращение внутренней энергии и на совершение системой работы на внешними телами. Это не означает, что всегда при сообщении тепла внутренняя энергия системы возрастает. Может случиться, что при сообщении системе тепла внутренняя энергия будет убывать
Данное уравнение выражает закон сохранения энергии и представляет собой содержание первого начала термодинамики: Количество тепла, сообщенное системе, идет на приращение внутренней энергии и на совершение системой работы на внешними телами. Это не означает, что всегда при сообщении тепла внутренняя энергия системы возрастает. Может случиться, что при сообщении системе тепла внутренняя энергия будет убывать 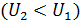 . В этом случае
. В этом случае  т.е система совершает работу за счет запаса внутренней энергии и за счет полученного тепла. Уравнение состояния идеального газа. Состояние заданной массы газа определяется значениями трех параметров: давления
т.е система совершает работу за счет запаса внутренней энергии и за счет полученного тепла. Уравнение состояния идеального газа. Состояние заданной массы газа определяется значениями трех параметров: давления 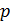 , объема
, объема  температуры
температуры  . Простейшими свойствами обладает газ взаимодействие, между молекулами которого пренебрежимо мало. Такой газ называется идеальным. При небольших плотностях газы с хорошей точностью подчиняются уравнению
. Простейшими свойствами обладает газ взаимодействие, между молекулами которого пренебрежимо мало. Такой газ называется идеальным. При небольших плотностях газы с хорошей точностью подчиняются уравнению  это и сеть уравнение состояния идеального газа. Обозначив соответствующую малую величину константы буквой R напишем уравнение
это и сеть уравнение состояния идеального газа. Обозначив соответствующую малую величину константы буквой R напишем уравнение 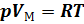
 объем занимаемый при данных
объем занимаемый при данных  молем газа.
молем газа. 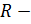 газовая постоянная (8,31 Дж/(моль∙К)). От уравнения для данного моля перейдем к уравнению для любой массы, приняв во внимание, что при одинаковом давлении и температуре
газовая постоянная (8,31 Дж/(моль∙К)). От уравнения для данного моля перейдем к уравнению для любой массы, приняв во внимание, что при одинаковом давлении и температуре  молей газа будут занимать в
молей газа будут занимать в  раз больший объем
раз больший объем  . Умножив уравнение
. Умножив уравнение 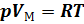 на
на  (
( 
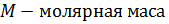 ) и заменив
) и заменив  на
на 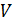
 Данное уравнение имеет и другие формы записи:
Данное уравнение имеет и другие формы записи:  (
( 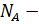 число Авогадро (
число Авогадро ( 
 постоянная Больцмана
постоянная Больцмана  ) так как
) так как 
 разделив обе части на объем и приняв то, что
разделив обе части на объем и приняв то, что 
 ;
;
Уравнение состояния идеального газа(уравнение Клапейрона — Менделеева)
 формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа
формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа
Работа и внутренняя энергия.
Работа и внутренняя энергия.
Таким образом, одним из процессов, приводящих к изменению внутренней энергии, является преобразование механической энергии во внутреннюю или наоборот. Работа является мерой изменения внутренней энергии при превращении механической энергии во внутреннюю или внутренней энергии в механическую.
точки зрения молекулярно-кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении.


А1 = р∆V – работа газа.
А1 = -А = р∆V – работа внешних сил.
Внутренняя энергия – это сумма кинетических энергий частиц (молекул, атомов) газа и зависит она только от температуры – т.е. интенсивности движения частиц газа, что и определяет их тепловое состояние. 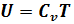 Для расчетов не столь важно знать, какова внутренняя энергия газа, а важно знать, на сколько она изменяется.
Для расчетов не столь важно знать, какова внутренняя энергия газа, а важно знать, на сколько она изменяется. 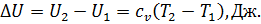 В отличие от жидкостей и твердых тел, Газообразные вещества способны значительно изменять свой объем. При этом силы давления совершают определенную механическую работу. Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A'. В то же время силы давления, действующие со стороны газа на поршень, совершают работу
В отличие от жидкостей и твердых тел, Газообразные вещества способны значительно изменять свой объем. При этом силы давления совершают определенную механическую работу. Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A'. В то же время силы давления, действующие со стороны газа на поршень, совершают работу  . Если объем газа изменился на малую величину ΔV, то газ совершает работу
. Если объем газа изменился на малую величину ΔV, то газ совершает работу  , где p – давление газа, S – площадь поршня,
, где p – давление газа, S – площадь поршня,  – его перемещение. При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
– его перемещение. При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:  или в пределе при
или в пределе при  → 0:
→ 0:  Теплоемкость. Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяемая отношением бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT:
Теплоемкость. Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяемая отношением бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT:  Единица измерения теплоёмкости в Международной системе единиц (СИ) — Дж/К. Физический смысл теплоемкости тела: теплоемкость тела равна количеству теплоты, поглощенному телом при нагревании или выделенному при его охлаждении на 1К. Удельная теплоемкость — это способность разных веществ к поглощению теплоты при их нагревании.
Единица измерения теплоёмкости в Международной системе единиц (СИ) — Дж/К. Физический смысл теплоемкости тела: теплоемкость тела равна количеству теплоты, поглощенному телом при нагревании или выделенному при его охлаждении на 1К. Удельная теплоемкость — это способность разных веществ к поглощению теплоты при их нагревании.
Удельная теплоемкость вещества определяется отношением количества теплоты, полученной им при нагревании, к массе вещества и изменению его температуры, если  :
:
Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:  Физический смысл молярной теплоемкости: молярная теплоемкость вещества, определяемая количеством теплоты, которое поглощается при нагревании или выделяется при охлаждении 1 моля вещества на 1 К.
Физический смысл молярной теплоемкости: молярная теплоемкость вещества, определяемая количеством теплоты, которое поглощается при нагревании или выделяется при охлаждении 1 моля вещества на 1 К.
Следовательно, молярную теплоемкость можно определить другим способом: 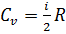 Удельная теплоемкость связана с молярной соотношением
Удельная теплоемкость связана с молярной соотношением  Уравнение Роберта Майера: молярная теплоемкость идеально- го газа при постоянном давлении равна сумме молярной теплоемкости этого газа при постоянном объеме и молярной газовой постоянной:
Уравнение Роберта Майера: молярная теплоемкость идеально- го газа при постоянном давлении равна сумме молярной теплоемкости этого газа при постоянном объеме и молярной газовой постоянной:  .
.
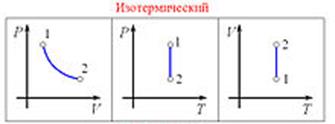 Изотермический процесс (Бойля Мариотта) Изотермический процесс — термодинамический процесс , происходящий в физической системе при постоянной температуре . Для осуществления изотермического процесса систему обычно помещают в термостат, теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро по сравнению со скоростью протекания процесса, и, температура системы в любой момент практически не отличается от температуры термостата. Графиком изотермического процесса является изотерма.
Изотермический процесс (Бойля Мариотта) Изотермический процесс — термодинамический процесс , происходящий в физической системе при постоянной температуре . Для осуществления изотермического процесса систему обычно помещают в термостат, теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро по сравнению со скоростью протекания процесса, и, температура системы в любой момент практически не отличается от температуры термостата. Графиком изотермического процесса является изотерма.
При изотермическом процессе системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа Теплоемкость и работа идеального газа в изотермическом процессе. Чтобы вычислить работу при изотермическом процессе, заменим давление в общей формуле 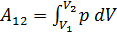 его выражением через другие величины в соответствии с уравнением состояния (
его выражением через другие величины в соответствии с уравнением состояния (  :). В результате получим (T можно вынести за знак интервала, поскольку она постоянна.
:). В результате получим (T можно вынести за знак интервала, поскольку она постоянна. 
В изотермическом процессе постоянна температура, то есть  . При изменении объёма газу передаётся (или отбирается) некоторое количество тепла. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности:
. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: 
Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. ТЕПЛОЕМКОСТЬ ИЗОХОРНЫЙ ПРОЦЕСС. ТЕПЛОЕМКОСТЬ И РАБОТА ИДЕАЛЬНОГО ГАЗА В ИЗОХОРНОМ ПРОЦЕССЕ.
 Изохорный процесс (Шарля). Изохорический или изохорный процесс— термодинамический процесс, который происходит при постоянном объёме
Изохорный процесс (Шарля). Изохорический или изохорный процесс— термодинамический процесс, который происходит при постоянном объёме  . Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. При изохорическом процессе давление идеального газа прямо пропорционально его температуре. Работу в этом процессе газ не совершает (т.к ΔV=0), соответственно Q= ΔU Уравнение изохорного процесса (уравнение Шарля) может быть записано в виде:
. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. При изохорическом процессе давление идеального газа прямо пропорционально его температуре. Работу в этом процессе газ не совершает (т.к ΔV=0), соответственно Q= ΔU Уравнение изохорного процесса (уравнение Шарля) может быть записано в виде: 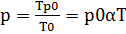 Где
Где  давление газа при T = T0 = 273 К.
давление газа при T = T0 = 273 К.  температурный коэффициент объемного расширения газа, равный 1/273 К-1 Энтропия процесса Т.к. в системе при изохорном процессе происходит теплообмен с внешней средой, то, соответственно, происходит изменение энтропии. Из определения энтропии следует:
температурный коэффициент объемного расширения газа, равный 1/273 К-1 Энтропия процесса Т.к. в системе при изохорном процессе происходит теплообмен с внешней средой, то, соответственно, происходит изменение энтропии. Из определения энтропии следует:  Где
Где  изменение энтропии
изменение энтропии 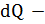 изменение энергии Теплоемкость и работа идеального газа в изохорном процессе. Работу в этом процессе газ не совершает (т.к ΔV=0), соответственно Q= ΔU Если нагревание происходит при постоянном объеме, тело не совершает работы над внешними телами и следовательно, согласно первому закону термодинамики все тепло идет на приращение внутренней энергии тела:
изменение энергии Теплоемкость и работа идеального газа в изохорном процессе. Работу в этом процессе газ не совершает (т.к ΔV=0), соответственно Q= ΔU Если нагревание происходит при постоянном объеме, тело не совершает работы над внешними телами и следовательно, согласно первому закону термодинамики все тепло идет на приращение внутренней энергии тела:  Из этого уравнения вытекает, что теплоемкость при постоянном объеме равна
Из этого уравнения вытекает, что теплоемкость при постоянном объеме равна  Такая запись подчеркивает то обстоятельство, что при дифференцировании выражения для
Такая запись подчеркивает то обстоятельство, что при дифференцировании выражения для  объем следует считать постоянным. В случае идеального газа
объем следует считать постоянным. В случае идеального газа  , так что выражение может быть преобразовано
, так что выражение может быть преобразовано 
Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. Теплоемкость. ИЗОБАРНЫЙ ПРОЦЕСС. ТЕПЛОЕМКОСТЬ И РАБОТА ИДЕАЛЬНОГО ГАЗА В ИЗОБАРНОМ ПРОЦЕССЕ.
 Изобарный процесс (Гей-Люссака).— термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе газа. Первый закон термодинамики для изобарного процесса записывается в виде:
Изобарный процесс (Гей-Люссака).— термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе газа. Первый закон термодинамики для изобарного процесса записывается в виде:  . При изобарическом процессе, давление в газе остается неизменным (
. При изобарическом процессе, давление в газе остается неизменным ( 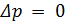 ). Объем идеального газа при изобарном процессе пропорционален температуре
). Объем идеального газа при изобарном процессе пропорционален температуре  .. Изменение энтропии в изобарном процессе, если изобарный процесс происходит идеальном газе, равен
.. Изменение энтропии в изобарном процессе, если изобарный процесс происходит идеальном газе, равен 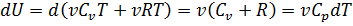 следовательно, изменение энтропии можно выразить как
следовательно, изменение энтропии можно выразить как 
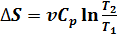 Теплоемкость и работа идеального газа в изобарном процессе. При изобарическом процессе работа совершается любым телом, в том числе и идеальным газом, как следует из уравнения
Теплоемкость и работа идеального газа в изобарном процессе. При изобарическом процессе работа совершается любым телом, в том числе и идеальным газом, как следует из уравнения 

Молярная теплоёмкость при постоянном давлении обозначается как Cp. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера  . где R - универсальная газовая постоянная - R=8.31 (Дж/(моль*К))
. где R - универсальная газовая постоянная - R=8.31 (Дж/(моль*К))
Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. ИЗОБАРНАЯ И ИЗОХОРНАЯ ТЕПЛОЕМКОСТИ. УРАВНЕНИЕ МАЙЕРА. ИЗОБАРНАЯ И ИЗОХОРНАЯ ТЕПЛОЕМКОСТИ В КИНЕТИЧЕСКОЙ ТЕОРИИ.
Уравнение Майера. Сравнение между собой Ср и СV приводит к уравнению Майера: 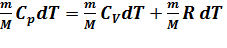 или
или  Вывод: при изобарическом нагревании газа к нему подводится больше теплоты, чем при изохорическом. Это уравнение показывает, что Ср больше, чем СV на величину универсальной газовой постоянной R. Это объясняется тем, что при изобарном нагревании газа, в отличие от изохорного нагревания, требуется дополнительное количество теплоты на совершение работы расширения газа. Таким образом, молярная теплоемкость газа определяется лишь числом степеней свободы и не зависит от температуры. Это утверждение справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней
Вывод: при изобарическом нагревании газа к нему подводится больше теплоты, чем при изохорическом. Это уравнение показывает, что Ср больше, чем СV на величину универсальной газовой постоянной R. Это объясняется тем, что при изобарном нагревании газа, в отличие от изохорного нагревания, требуется дополнительное количество теплоты на совершение работы расширения газа. Таким образом, молярная теплоемкость газа определяется лишь числом степеней свободы и не зависит от температуры. Это утверждение справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней  свободы, проявляющееся в теплоемкости, зависит от температуры. Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Полезно знать формулу Майера для удельных теплоёмкостей:
свободы, проявляющееся в теплоемкости, зависит от температуры. Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Полезно знать формулу Майера для удельных теплоёмкостей:  .
.
Изобарная и изохорная теплоемкости в кинетической энергии. Процессы с подводом теплоты при постоянном давлении называется изобарными, а с подводом теплоты при постоянном объеме – изохорным. При теплотехнических расчетах в зависимости от процессов теплоемкости получают соответствующие названия:  изохорная теплоемкость,
изохорная теплоемкость,  изобарная теплоемкость.Теплоемкость при изобарном процессе
изобарная теплоемкость.Теплоемкость при изобарном процессе  При изохорном процессе:
При изохорном процессе:  Уравнение Майера:
Уравнение Майера:  или
или  – показывает связь между изобарным и изохорным процессами. (Вывод: при изобарическом нагревании газа к нему подводится больше теплоты, чем при изохорическом.) В процессах
– показывает связь между изобарным и изохорным процессами. (Вывод: при изобарическом нагревании газа к нему подводится больше теплоты, чем при изохорическом.) В процессах  работа не совершается, а полностью расходуется на изменение внутренней энергии
работа не совершается, а полностью расходуется на изменение внутренней энергии  , при изобарном подвод теплоты имеет место увеличение внутренней энергии и совершение работы против внешних сил, поэтому изобарная теплоемкость Ср всегда больше изохорной на величину газовой постоянной R. Истинная молярная теплоемкость
, при изобарном подвод теплоты имеет место увеличение внутренней энергии и совершение работы против внешних сил, поэтому изобарная теплоемкость Ср всегда больше изохорной на величину газовой постоянной R. Истинная молярная теплоемкость  – это отношение бесконечно малого количества теплоты, сообщенной 1 моль вещества при определенной температуре, к приращению температуры, которое при этом наблюдается:
– это отношение бесконечно малого количества теплоты, сообщенной 1 моль вещества при определенной температуре, к приращению температуры, которое при этом наблюдается:  Согласно уравнению
Согласно уравнению  , теплоемкость , как и теплота, не является функцией состояния. При постоянном давлении или объеме, согласно уравнениям (11) и (12), теплота, а, следовательно, и теплоемкость приобретают свойства функции состояния, то есть становятся характеристическими функциями системы. Таким образом, получаем изохорную и изобарную теплоемкости .
, теплоемкость , как и теплота, не является функцией состояния. При постоянном давлении или объеме, согласно уравнениям (11) и (12), теплота, а, следовательно, и теплоемкость приобретают свойства функции состояния, то есть становятся характеристическими функциями системы. Таким образом, получаем изохорную и изобарную теплоемкости .
Изохорная теплоемкость  – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1
– количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1  , если процесс происходит при
, если процесс происходит при  .
. 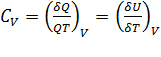 .
.
Изобарная теплоемкость 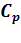 – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1
– количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1  при
при  :
: 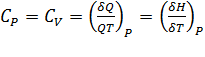 . Теплоемкость зависит не только от температуры, но и от объема системы, поскольку между частицами существуют силы взаимодействия, которые изменяются при изменении расстояния между ними, поэтому в уравнениях (
. Теплоемкость зависит не только от температуры, но и от объема системы, поскольку между частицами существуют силы взаимодействия, которые изменяются при изменении расстояния между ними, поэтому в уравнениях ( 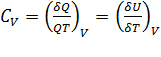 ) и (
) и ( 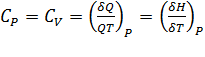 . ) используют частные производные. В соответствии с молекулярно-кинетической теорией идеальных газов их изобарные и изохорные теплоемкости величины постоянные, не зависящие от термических параметров состояния газа.
. ) используют частные производные. В соответствии с молекулярно-кинетической теорией идеальных газов их изобарные и изохорные теплоемкости величины постоянные, не зависящие от термических параметров состояния газа.
Первое начало термодинамики. Уравнение состояния идеального газа. Работа и внутренняя энергия. ТЕПЛОЕМКОСТЬ АДИАБАТНЫЙ ПРОЦЕСС. УРАВНЕНИЕ ПУАССОНА. ТЕПЛОЕМКОСТЬ И РАБОТА ИДЕАЛЬНОГО ГАЗА В АДИАБАТНОМ ПРОЦЕССЕ.
Адиабатный— отсутствие теплообмена между рабочим телом и внешней средой.
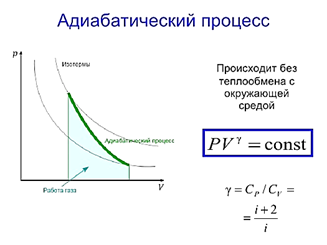 Адиаба́тный проце́сс— термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной и изменения энтропии не происходит. Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона . Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена (
Адиаба́тный проце́сс— термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной и изменения энтропии не происходит. Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона . Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена ( 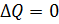 ) системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид
) системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид  где
где  — изменение внутренней энергии тела,
— изменение внутренней энергии тела,  — работа, совершаемая системой. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит:
— работа, совершаемая системой. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит:  Здесь
Здесь  — температура системы,
— температура системы, 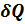 — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла.
— теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла.
Уравнение Пуассона. Найдем уравнение связывающее параметры идеального газа при адиабатическом процессе. Подставим в первое начало термодинамики выражение  для идеального газа
для идеального газа 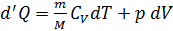 .
.
Так как для адиабатического процесса 
 . Теперь выразим
. Теперь выразим 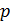 через
через 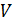 и
и  в соответствии уравнения состояния идеального газа
в соответствии уравнения состояния идеального газа 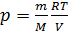 , и подставим это выражение в
, и подставим это выражение в  в результате сокращая отличный от 0 множитель
в результате сокращая отличный от 0 множитель  получаем:
получаем:  . Преобразуем полученное выражение следующим образом
. Преобразуем полученное выражение следующим образом  Последнее соотношение можно записать в виде
Последнее соотношение можно записать в виде  откуда следует что при адиабатическом процессе
откуда следует что при адиабатическом процессе  Отношение
Отношение  можно заменить через
можно заменить через 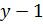
 . Произведя такую замену в последнем уравнении получим:
. Произведя такую замену в последнем уравнении получим:  Полученное соотношение представляет собой уравнение адиабаты идеального газа в параметрах :
Полученное соотношение представляет собой уравнение адиабаты идеального газа в параметрах :  От этого уравнения можно перейти к уравнению в параметрах
От этого уравнения можно перейти к уравнению в параметрах 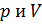 , заменив в нем
, заменив в нем  через
через 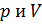 в соответствии с уравнением состояния идеального газа:
в соответствии с уравнением состояния идеального газа:  Подставив это выражение в уравнение
Подставив это выражение в уравнение 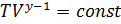 и учтя
и учтя 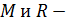 постоянные получим
постоянные получим  Данное соотношение называется уравнением адиабаты идеального газа или уравнением Пуассона. Данное уравнение можно записать в виде:
Данное соотношение называется уравнением адиабаты идеального газа или уравнением Пуассона. Данное уравнение можно записать в виде: 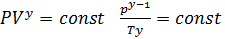
Теплоемкость и работа идеального газа в адиабатическом процессе. В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть  . Однако, объём, давление и температура меняются, то есть
. Однако, объём, давление и температура меняются, то есть  .Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю:
.Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю:  .
.
Работа которая совершается при переходе из состояния 1 в состояние 2 каким – либо телом над внешними телами равна  Выражая
Выражая  для произведения интегрирования и последующей подстановки получившихся выражений в исходную формулу даст нам формулы для вычисления идеального газа при адиабатическом процессе
для произведения интегрирования и последующей подстановки получившихся выражений в исходную формулу даст нам формулы для вычисления идеального газа при адиабатическом процессе 
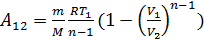
ПОЛИТРОПНЫЙ ПРОЦЕСС. УРАВНЕНИЕ ПОЛИТРОПЫ. ПОКАЗАТЕЛЬ ПОЛИТРОПЫ. РАБОТА В ПОЛИТРОПНОМ ПРОЦЕССЕ. ПОКАЗАТЕЛЬ ПОЛИТРОПЫ И ТЕПЛОЕМКОСТЬ ПРОЦЕССА. ПРОЦЕССЫ С ОТРИЦАТЕЛЬНОЙ ТЕПЛОЕМКОСТЬЮ.
Политропическим называется процессы, при которых теплоемкость тела остается постоянной. Таким образом, условие, которые выполняется в ходе политропического процесса, заключается в том, что  Если теплоемкость зависит от температуры, то нужно найти среднюю теплоемкость, чтобы процесс стал политропным. Уравнение полтиропы. Найдем уравнение политропы для идеального газа. Напишем уравнение первого начала для одного моля газа, представив
Если теплоемкость зависит от температуры, то нужно найти среднюю теплоемкость, чтобы процесс стал политропным. Уравнение полтиропы. Найдем уравнение политропы для идеального газа. Напишем уравнение первого начала для одного моля газа, представив  в виде
в виде  а
а  в виде
в виде 
 Все три параметра
Все три параметра 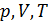 можно исключить с помощью уравнения состояния.
можно исключить с помощью уравнения состояния. 
 уравнение политропы, где
уравнение политропы, где 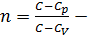 показатель политропы. Показатель политропы. Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Показателем же политропы является величина, характеризующая политропный процесс относительно определенного интервала или значения в котором находиться
показатель политропы. Показатель политропы. Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Показателем же политропы является величина, характеризующая политропный процесс относительно определенного интервала или значения в котором находиться 
 Показатель политропы находиться из уравнения
Показатель политропы находиться из уравнения  . Здесь
. Здесь  — теплоёмкость газа в данном процессе,
— теплоёмкость газа в данном процессе, 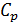 и
и  — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.
— теплоемкости того же газа, соответственно, при постоянном давлении и объеме.
В зависимости от вида процесса, можно определить значение n:
•Изотермический процесс:  , так как
, так как  , значит, по закону Бойля — Мариотта
, значит, по закону Бойля — Мариотта  , и уравнение политропы вынуждено выглядеть так:
, и уравнение политропы вынуждено выглядеть так: 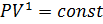 . •Изобарный процесс:
. •Изобарный процесс:  , так как
, так как  , и уравнение политропы вынуждено выглядеть так:
, и уравнение политропы вынуждено выглядеть так:  .
.
•Адиабатный процесс: 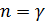 (здесь
(здесь  — показатель адиабаты), это следует из уравнения Пуассона. •Изохорный процесс:
— показатель адиабаты), это следует из уравнения Пуассона. •Изохорный процесс:  , так как
, так как  , и в процессе
, и в процессе  , а из уравнения политропы следует, что
, а из уравнения политропы следует, что  , то есть, что
, то есть, что 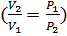 , то есть
, то есть 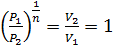 , а это возможно, только если
, а это возможно, только если 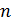 является бесконечным.
является бесконечным.
Работа в политропном процессе. 
Теплоемкость политропных процессов

Теплоемкость политропного процесса  можно определить из выражения
можно определить из выражения

 = n
= n 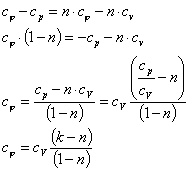
где k - показатель адиабаты.
Найдем значение 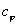 и n для изопроцессов определения сведем результаты в таблицу
и n для изопроцессов определения сведем результаты в таблицу
| процесс | 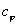
| n |
| T=const | 
| 1 |
| p=const | 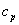
| 0 |
| v=const | 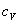
| 
|
| q=const | 0 | k |
Изобразим зависимость 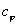 (n) графически
(n) графически
В деапазоне 1<n<k теплоемкость процессов отрицательная, т.е. с подводом теплоты температура системы уменьшается, а с отводом теплоты - увеличивается.
Смысл отрицательной теплоемкости заключается в том, что вся подведенная теплота расходуется на работу и, кроме этого, на работу затрачивается еще и часть внутренней энергии системы.
Теплоемкость является положительной величиной, если при получении тепла система разогревается и, наоборот, если система, отдавая тепло , охлаждается . Однако теплоемкость может быть и отрицательной. Это, как видно из формулы наблюдается в двух случаях:
1) при получении тепла система охлаждается ,
2) при отдаче тепла система разогревается. 
В первом случае газ производит работу расширения 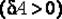 в количестве большем, чем количество теплоты
в количестве большем, чем количество теплоты  , которое подводится к газу в процессе расширения
, которое подводится к газу в процессе расширения  . В этом случае на производство работы помимо тепла, подведенного к газу, расходуется и некоторое количество его внутренней энергии. Хотя к газу и подводится тепло, но оно целиком превращается в работу, а убыль внутренней энергии
. В этом случае на производство работы помимо тепла, подведенного к газу, расходуется и некоторое количество его внутренней энергии. Хотя к газу и подводится тепло, но оно целиком превращается в работу, а убыль внутренней энергии  газа ведет к снижению температуры.
газа ведет к снижению температуры.
Во втором случае работа, производимая над газом при его сжатии  , оказывается по абсолютной величине большей, чем количество отдаваемого им тепла . С учетом знаков количества теплоты
, оказывается по абсолютной величине большей, чем количество отдаваемого им тепла . С учетом знаков количества теплоты  и работы
и работы 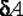 равенство принимает вид:
равенство принимает вид:

Внутренняя энергия системы увеличивается, а значит, ее температура растет, несмотря на то, что газ отдает теплоту. Подобный процесс происходит в некоторых звездах: гравитационные силы при сжатии звезды совершают работу большую, чем излучаемое ей тепло, поэтому звезда разогревается, несмотря на то, что она излучает теплоту. Наконец, обратим внимание на размерность теплоемкости. В системе СИ ее размерностью, как видно из формулы, является 

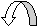
dq=du+dl подвод тепла dq=du+dl отвод тепла



ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ ГАЗОВОЙ МОЛЕКУЛЫ. ПОСТУЛАТ МАКСВЕЛЛА. СРЕДНЯЯ ЭНЕРГИЯ ХАОТИЧЕСКОГО ДВИЖЕНИЯ МОЛЕКУЛЫ. ПОСТОЯННАЯ БОЛЬЦМАНА И УНИВЕРСАЛЬНАЯ ГАЗОВАЯ ПОСТОЯННАЯ. МОЛЯРНЫЕ ТЕПЛОЕМКОСТИ ИДЕАЛЬНОГО ГАЗА.
Дата добавления: 2018-11-24; просмотров: 3567; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
