Внутренняя энергия идеального газа.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии: 
Где: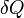 
— подведённая к телу теплота, измеренная в джоулях
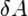— работа, совершаемая телом против внешних сил, измеренная в джоулях
В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна 
Так как в одном киломоле содержится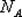 
молекул, то внутренняя энергия одного киломоля газа будет 
Учитывая, что 
, получим 
Для любой массы m газа, т.е. для любого числа киломолей 
внутренняя энергия 
Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю.
Равномерное распределение энергии по степеням свободы газовой молекулы. Итак, средняя энергия приходящаяся на одну степень свободы: 
У одноатомной молекулы i = 3, тогда для одноатомных молекул 
для двухатомных молекул 
для трёхатомных молекул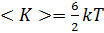 
|
|
|
Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится 
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы. Если система находится в состоянии термодинамического равновесия, при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы. На каждую поступательную iп и вращательную iвр степени свободы приходится энергия 1/2 kT. Для колебательной iкол, степени свободы она равна kT. Таким образом число степеней свободы i = iп + iвр + 2iкол
Постулат Максвелла – равное распределение.
Согласно молекулярно-кинетической теории – как бы не изменялись скорости отдельных частиц, средняя квадратичная скорость молекулы остается постоянной и равна v кв = 
= 
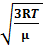; Это объясняется тем, что в газе, находящимся в состоянии термодинамического равновесия, устанавливается некоторое стационарное, независящее от времени, распределение молекул по скоростям.
|
|
|
Закон распределения молекул по скоростям впервые был выведен Максвелом. При выводе этого закона предполагалось, что газ состоит из состоит из очень большого числа частиц N, которые находятся в состоянии хаотического теплового движения, предполагалось, что никакие силовые поля на частицы газа не действуют. Закон Максвела описывает некоторую функцию, называемую функцией распределения молекул по скоростям.
Так, мы получили 
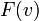- функцию плотности вероятности, которая и называется распределением Максвелла.
Условия применимости распределения Максвелла:
1. Равновесное состояние системы, состоящей из большого числа частиц.
2. Изотропная система, то есть реальная система.
3. Классическая система. Это значит, что система должна быть не релятивистской и не квантовой (взаимодействие частиц допускается, но только зависящее от относительного положения частиц).
<Ɛ i > = 
<Ɛпост> = 
Средняя энергия хаотического движения молекулы.
|
|
|
Интересно отметить, что средняя энергия теплового движения молекул зависит только от температуры газа. При данной температуре средняя кинетическая энергия поступательного хаотического движения молекул не зависит ни от химического состава газа, ни от массы молекул, ни от давления газа, ни от объема, занимаемого газом. Постоянная Больцмана и универсальная газовая постоянная.
Универсальная газовая постоянная численно равна работе расширения одного моля идеального одноатомного газа в изобарном процессе при увеличении температуры на 1 К. Универсальная газовая постоянная более удобна при расчетах, когда число частиц задано в молях. R=kNa Постоянная Больцмана (k) — физическая постоянная , определяющая связь между температурой вещества и энергией теплового движения частиц этого вещества. Её экспериментальное значение в системе СИ равно 
Дж/К. Постоянная Больцмана может быть получена из определения абсолютной температуры и других физических постоянных. Существует связь между универсальной газовой постоянной 
и числом Авогадро 
, из которой следует значение постоянной Больцмана ( Универсальная газовая постоянная выражается через произведение постоянной Больцмана на число Авогадро, 
): 
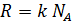Размерность постоянной Больцмана такая же, как и у энтропии. ДЖ/К
|
|
|
Дата добавления: 2018-11-24; просмотров: 476; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!