ЭНТРОПИЯ И СВОБОДНАЯ ЭНЕРГИЯ. СВЯЗАННАЯ ЭНЕРГИЯ. Второе начало термодинамики и направление процесса. Закон возрастания энтропии. Идеальная тепловая машина и возрастание энтропии.

⇐ ПредыдущаяСтр 6 из 18Следующая ⇒

Энтропия и свободная энергия. Свободная энергия есть та работа, которую могло бы совершить тело в обратимом изотермическом процессе, или свободная энергия есть максимальная возможная работа, которую может совершить система, обладая каким-то запасом внутренней энергии. Свободная энергия в любой системе заключена в виде потенциальной энергии. Чем больше система содержит свободной энергии, тем большую работу она может совершить. Так, более разряженный газ содержит меньше свободной энергии и больше связанной, чем сжатый газ при той же температуре. Следовательно, сжатый газ способен совершить больше полезной работы. В ходе химической реакции свободная энергия уменьшается и при данных условиях достигает минимального значения, а система становится термодинамически устойчивой. Это соответствует состоянию равновесия. При изменении внешних условий равновесие тотчас же сместится, а в системе самопроизвольно возникнут процессы, которые вновь приведут свободную энергию к минимальному для данных условий уровню. Следовательно, состояние системы, соответствующее минимуму свободной энергии, является состоянием устойчивого равновесия при данных условиях: 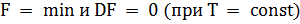Из вышеизложенного можно сделать вывод: в изолированных системах самопроизвольно могут протекать только процессы, направленные в сторону понижения свободной энергии системы – это принцип минимума свободной энергии. Если DF > 0, то процесс идет самопроизвольно в обратном направлении; если DF < 0, то процесс идет самопроизвольно в прямом направлении; если DF = 0, то это состояние равновесия и система достигает минимум свободной энергии. Величина непроизводительной, то есть, «обесцененной» части энергии ТS тем больше, чем меньше разность температур в системе. Мерой такого «обесценения» энергии является термодинамическая функция состояния, названная Клаузиусом энтропией (от греч. «обращать внутрь»). Эта функция в термодинамике обозначается S. Энтропия – это термодинамическая функция состояния, которая служит мерой неупорядоченности (беспорядка) состояния системы. Состояние системы можно характеризовать микросостояниями составляющих ее частиц, то есть, их мгновенными координатами и скоростями различных видов движения в различных направлениях. Число микросостояний системы называется термодинамической вероятностью системы (W). Для одного моля вещества 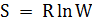, поэтому энтропия имеет ту же размерность, что и молярная постоянная R – Дж/(мольК).

Связанная энергия – та часть внутренней энергии, которая не может быть превращена в работу, – это обесцененная часть внутренней энергии. При одной и той же температуре связанная энергия тем больше, чем больше энтропия.
Таким образом, энтропия системы есть мера обесцененности ее энергии (т.е. мера той энергии, которая не может быть превращена в работу).
В термодинамике есть еще понятие – энергетическая потеря в изолированной системе: 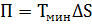где T_мин - температура окружающей среды. При любом необратимом процессе энтропия увеличивается до того, пока не прекратятся какие-либо процессы, т.е. пока не станет F = 0. И это произойдет при достижении замкнутой системой равновесного состояния, т.е. когда все параметры состояния системы (Р, Т) во всех точках системы станут одинаковыми. Вывести систему из этого равновесного состояния, можно только затратив энергию извне.

Приведенная теплота и энтропия. РАСЧЕТ ИЗМЕНЕНИЯ ЭНТРОПИИ В ИЗОБАРНОМ ПРОЦЕССЕ. Энтропия и термодинамическая вероятность. ФОРМУЛА БОЛЬЦМАНА. Вероятностный смысл второго начала термодинамики.

Приведенная теплота и энтропия. Расчет изменения энтропии в изобарном процессе. Изменение энтропии при изобарном процессе равно 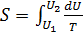В случае, если изобарный процесс происходит в идеальном газе, то 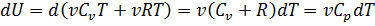следовательно, изменение энтропии можно выразить как 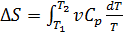Если пренебречь зависимостью 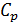от температуры (это предположение справедливо, например, для идеального одноатомного газа, но в общем случае не выполняется), то 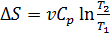Энтропия и термодинамическая вязкость. Второе начало термодинамики утверждает, что все необратимые процессы идут так, что энтропия участвующих в них тел возрастает, стремясь к максимальному значению. Максимальное значение энтропии достигается тогда, когда система приходит в равновесное состояние. Переход к равновесному состоянию является значительно более вероятным по сравнению со всеми другими переходами. Поэтому и наблюдаются только те изменения состояния, при которых система переходит из менее вероятного в более вероятное состояние (термодинамическая вероятность возрастает). Обращает на себя внимание поразительное сходство в поведении двух величин – энтропии и термодинамической вероятности: обе они участвуют при переходе системы к равновесию. Кроме этого, экспериментальные исследования показывают, что макроскопические свойства системы определяются ее микроскопическими свойствами. Поэтому естественно допустить существование связи между энтропией и термодинамической вероятностью. 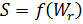О логарифмической зависимости между энтропией и термодинамической вероятностью можно сделать вывод на основе следующих соображений. Из определения энтропии ясно, что энтропия любого вещества пропорциональна массе. Это значит, что энтропия всей системы равна сумме энтропий ее отдельных частей. Разделим вещество на две части, тогда, очевидно, что 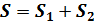По законам теории вероятности вероятность данного состояния всей массы вещества равна произведению вероятностей состояния его отдельных частей, то есть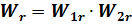

Таким образом, суммированию энтропий соответствует умножение термодинамических вероятностей отдельных частей. Энтропия пропорциональна натуральному логарифму термодинамической вероятности. Отметим еще в связи с этим, что хотя между энтропией и термодинамической вероятностью существует установленная связь, однако описание изменения состояния системы через изменение ее энтропии имеет то преимущество, что энтропия легко выражается через макроскопические параметры, тогда как вычисление термодинамической вероятности часто сопряжено с большими трудностями. Изолированная система, будучи введена из состояния равновесия, переходит в состояние равновесия как наиболее вероятное. Но молекулярная статистика допускает, что система из наиболее вероятного состояния (равновесного) может самопроизвольно перейти в менее вероятное (неравновесное) состояние. Однако, как выше уже отмечалось, вероятность значительного отклонения от равновесного состояния исчезающе мала. Но чем меньше отклонение, тем оно более вероятно. Поэтому незначительные отклонения в системе всегда имеют место. Поскольку энтропия связана с термодинамической вероятностью, также не исключено самопроизвольное отклонение энтропии в сторону ее уменьшения. Существенное же уменьшение энтропии маловероятно, хотя незначительные флуктуации неизбежны. Поэтому более точная формулировка второго начала утверждает: в изолированной системе возрастание энтропии наиболее вероятно.

Формула Больцмана. Связь между термодинамической вероятностью состояния системы и ее энтропией была установлена в 1875 г. двумя знаменитыми учеными – Д. Гиббсом и Л. Больцманом. Эта связь выражается формулой Больцмана, которая имеет вид: 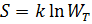где 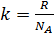, R – универсальная газовая постоянная, N_A – число Авогадро. Теоретическое значение формулы Больцмана огромно. В частности, формула дает основание рассматривать второе начало термодинамики как статистический закон. Тем самым создается прицельно новое (по сравнению с термодинамикой) понимание второго начала и природы необратимости. Вероятностный смысл второго начала термодинамики. В результате глубокого анализа Л.Больцман установил связь между вероятностью состояния и энтропией системы частиц. Эта связь выражается формулой Больцмана: S = k · ln P_ТД. Здесь 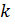– постоянная Больцмана (k = 1,37^.10^–23 Дж.К^–1), а Р_ТД – термодинамическая вероятностьданного состояния системы.

Термодинамическая вероятность – это число вариантов расположения молекул и распределения их скоростей, соответствующая данному состоянию системы. По самому смыслу понятия вероятности любая система, предоставленная сама себе (то есть изолированная), будет переходить из состояния с меньшей вероятностью в состояние, вероятность которого больше. Обратный переход в принципе возможен, но практически невероятен. Учитывая формулу Больцмана, мы сразу приходим к формулировке второго начала термодинамики: все реальные процессы в изолированной системе происходят в сторону состояний с большей вероятностью, то есть с увеличением энтропии. Таким образом, второе начало является вероятностным законом.

Приведенная теплота и энтропия. РАСЧЕТ ИЗМЕНЕНИЯ ЭНТРОПИИ В ИЗОХОРНОМ ПРОЦЕССЕ. Энтропия и термодинамическая вероятность. Формула Больцмана. Вероятностный смысл второго начала термодинамики.

Расчет изменения энтропии в изобарном процессе.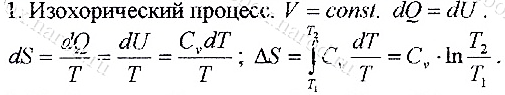

17. Приведенная теплота и энтропия. РАСЧЕТ ИЗМЕНЕНИЯ ЭНТРОПИИ В ИЗОТЕРМИЧЕСКОМ ПРОЦЕССЕ. Энтропия и термодинамическая вероятность. Формула Больцмана. Вероятностный смысл второго начала термодинамики.

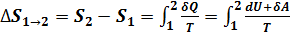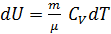
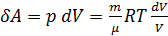
Расчет изменения энтропии в изотермическом процессе. Если система совершает равновесный переход из состояния 1 в состояния 2, то изменения энтропии .Найдем изменение энтропии в процессах идеального газа. 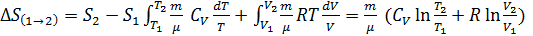т.е. изменения энтропии S ΔS_1→2идеального газа при переходе его из состояния 1 в состояния 2 не зависит от вида процесса.

При изотермическом процессе (T = const; T₁ = T₂: )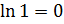

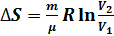
Дата добавления: 2018-11-24; просмотров: 2493; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!