Состояние механической системы. Законы Ньютона. Уравнения движения и начальные Движение тела в диссипативной среде. Время и путь релаксации. Мгновенная мощность рассеяния.
Движение тела в диссипативной среде
Движение тела массой m под действием постоянной силы F при наличии сопротивления среды описывается следующим уравнением:
.
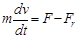В такой среде действует сила вязкого трения.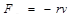 
,
r – коэффициент сопротивления, зависящий от формы, размеров тела и от вязкости среды h. Для шара радиуса R коэффициент сопротивления определяется формулой Стокса
.
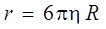При движении тела в вязкой среде происходит рассеяние (диссипация) его кинетической энергии. Слои жидкости, находящиеся на разном расстоянии от движущегося тела имеют различную скорость. Слой жидкости, находящийся в непосредственной близости от поверхности движущегося тела, имеет ту же скорость, что и тело, по мере удаления скорость частиц жидкости уменьшается. В этом состоит явление вязкого трения, в результате которого энергия тела передается слоям окружающей среды в направлении, перпендикулярном движению тела.
В данной работе тело движется под действием силы тяжести, уменьшенной в результате действия выталкивающей силы Архимеда, т.е.
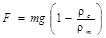
где rс и rт – плотности среды и тела, соответственно. Таким образом, уравнение движения преобразуется к виду
.
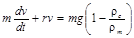Путь и время релаксации (см. в тетради)
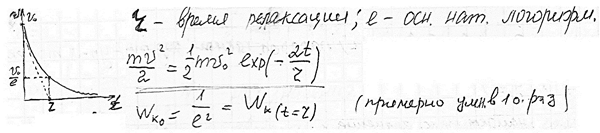
Мгновенная мощность - предел, к которому стремится средняя мощность за бесконечно малый промежуток времени. (формулу см. в тетради)
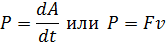
Гармонические колебания. Уравнение движения. Амплитуда, частота и фаза колебании, связь начальными условиями. Скорость и ускорение при гармонических колебаниях.
|
|
|
Колебательное движение – точка через равные промежутки времени проходит через одно и то же положение в одном направлении.
Гармонические колебания, колебания, при которых физическая величина изменяется с течением времени по закону синуса или косинуса.
Уравнение движе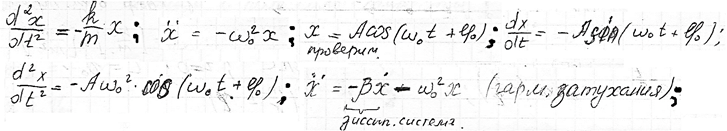ния 
Выражение, стоящее под знаком cos или sin, наз. фазой колебания.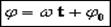 
Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
Амплитуда колебания (максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении) зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Частота — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени.
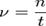
Скорость и ускорение
Согласно определению скорости, скорость – это производная от координаты по времени
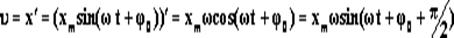
Скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2
|
|
|
Величина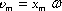 
- максимальная скорость колебательного движения (амплитуда колебаний скорости).
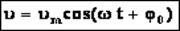
Ускорение – это производная от скорости по времени
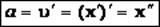
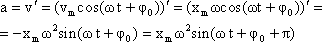
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения на p
Часто бывает удобно записывать уравнения для колебаний в виде: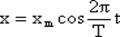 
, где T – период колебания.
Дата добавления: 2018-11-24; просмотров: 841; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!