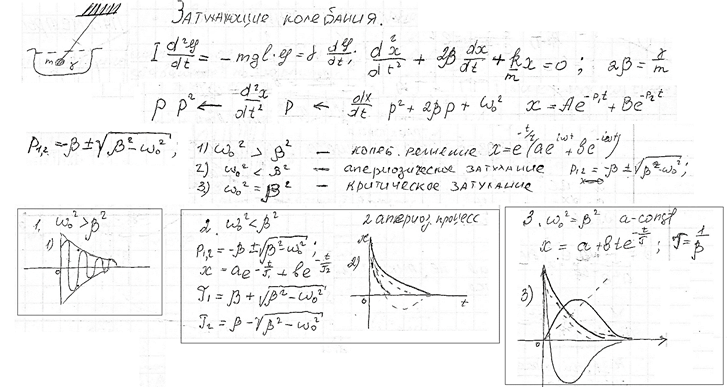
Затухающие колебания пружинного маятника. Апериодический и колебательный процесс. Критическое затухание. Время релаксации, декремент затухания и добротность.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени.
Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
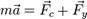
где Fc — сила сопротивления, Fy — сила упругости
Fc = − cv, Fy = − kx, то есть
ma + cv + kx = 0
или в дифференциальной форме
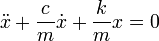
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
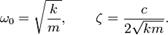
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
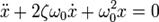
АПЕРИОДИЧЕСКИЙ ПРОЦЕСС – очень сильное затухание.
Если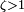 
, то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
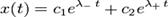В этом случае колебания с самого начала экспоненциально затухают.
Критическое затухание - затухание на границе апериодичности. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение.
Декремент затухания - количественная характеристика быстроты затухания колебаний.
Добротность - характеристика колебательной системы, показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
|
|
|
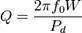
где:f0 — резонансная частота колебаний; W — энергия, запасённая в колебательной системе; Pd — рассеиваемая мощность;
Релаксация в диссипативной среде - характеристика процесса установления равновесия термодинамического в макроскопич. физ. системе, период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз.
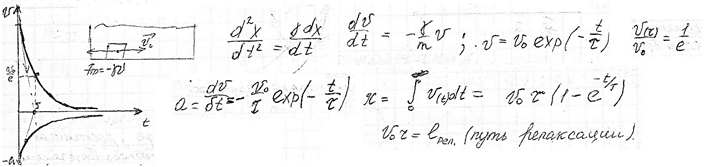
Система материальных точек. Степени свободы. Центр масс (центр инерции). Движение системы материальных точек. Сохранение импульса.
Система материальных точек - совокупность точек, рассматриваемых как единое целое.
Силы, с которыми взаимодействуют материальные точки системы между собой, называют внутренними силами. Силы, с которыми на материальные точки системы действуют тела, не входящие в данную систему (внешние тела), называют внешними силами.
Степени свободы для материальной точки или частицы – понимают число независимых уравнений, которыми можно описать движение частицы. (i=3)
Если две частицы связаны жесткой связью, то число уравнений степеней свободы уменьшается на одно.
Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных, необходимых для полного описания движения механической системы:
|
|
|
*Материальная точка в трёхмерном пространстве — обладает тремя степенями свободы, так как её состояние полностью описывается тремя пространственными координатами.
*Абсолютно твёрдое тело обладает шестью степенями свободы, так как для полного описания положения такого тела достаточно задать три координаты центра масс и три угла, описывающих ориентацию тела.
*Реальные тела обладают огромным числом степеней свободы (порядка числа частиц, из которых состоит тело). Однако в большинстве ситуаций оказывается, что наиболее важны лишь несколько «коллективных» степеней свободы, характеризующих движение центра масс тела, его вращение, его деформацию, его макроскопические колебания. Остальные же — микроскопические — степени свободы не заметны по отдельности, а воспринимаются сразу все вместе, как, например, температура и давление.
Центр масс
Центр масс, центр инерции, геометрическая точка, положение которой характеризует распределение масс в теле или механической системе. Координаты Ц. м. определяются формулами:
|
|
|
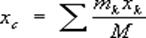
Движение системы точек
При движении материальных точек системы центр масс перемещается. Определим, от чего зависит характер движения центра масс. Следовательно, центр масс замкнутой системы материальных точек движется равномерно и прямолинейно либо остается неподвижным независимо от того, как движутся отдельные материальные точки системы.
Сохранение импульса
Зако́н сохране́ния и́мпульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
Дата добавления: 2018-11-24; просмотров: 849; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!