Сохранение импульса. Упругий нецентральный удар двух шаров.
Упругий удар
Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой. Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей после удара нужно знать положение линии центров в момент удара или расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости налетающего шара. Если массы шаров одинаковы, то векторы скоростей и шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
|
|
|
Система материальных точек. Степени свободы. Центр масс (центр инерции). Движение системы материальных точек. Поступательное движение и вращение. Сохранение момента импульса.
Центр масс (центр инерции) – средняя точка положения, которой определена средним значением координат, взятых с весовыми коэффициентами равным массам частиц.
Момент силы – Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело
Поступательное движение и вращение – если точки перемещаются параллельно самой себе.
Если при движении твердого тела можно найти точку для которой радиус векторы проведенные из этой точки в произвольную точку тела, описывают окружности (с общим центром), то такое движение называется вращением, а точка называется центром вращения.
Если через центр вращения можно провести прямую, то в проекции всех радиус векторов, проведенных из центра вращения, на направление перпендикулярное данной прямой, так же описывает окружности, центры которых на прямой, то такая прямая называется осью вращения.
|
|
|
Сохранение момента импульса - Зако́н сохране́ния моме́нта и́мпульса— векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
Движение системы частиц.
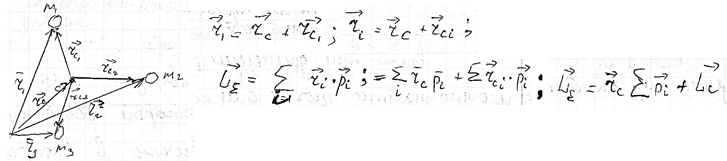
Сохранение момента импульса
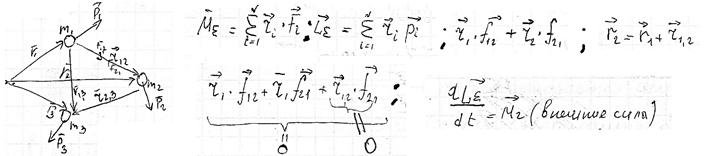
Работа силы и кинетическая энергия. Силовое поле. Работа сил поля и потенциальная энергия. Консервативные силы и потенциальные поля. Связь силы и потенциальной энергии. Сохранение энергии.
Работа силы – физическая величина, равная произведению силы на перемещение.
Кинетическая энергия - энергия механической системы, зависящая от скоростей движения её точек. Работа и Кинетическая энергия.
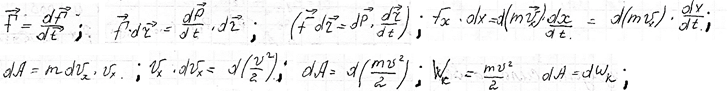
Силовое поле - часть пространства (ограниченная или неограниченная), в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила, зависящая или только от координат x, у, z этой точки, или же от координат x, у, г и времени t. В первом случае С. п. называется стационарным, а во втором — нестационарным. Если сила во всех точках С. п. имеет одно и то же значение, т. е. не зависит ни от координат, ни от времени, то С. п. называется однородным.
|
|
|
Работа сил поля и потенциальная энергия
Полная энергия тела: W=Wp+Wk;
Дата добавления: 2018-11-24; просмотров: 2427; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!