Распределение Больцмана. Барометрическая формула.

Распределение Больцмана.

Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения , падает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов. Исходя из основного уравнения молекулярно-кинетической теории: 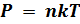, заменим P и P₀ в барометрической формуле (2.4.1) на n и n₀ и получим распределение Больцмана для молярной массы газа: где n₀ и n - число молекул в единичном объёме на высоте h = 0 и h.

Так как а , то можно представить в виде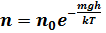

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии: – это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0. Барометрическая формула. Атмосферное давление на какой – либо высоте обусловлено весом вышележащих слоев газа. Обозначим буквой давление на высоте тода давление на высоте будет , причем, если больше нуля, то меньше нуля, так как вес вышележащих слоев атмосферы, а следовательно и давление убывают. Разность давлений 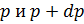равна весу газа, заключенного в объеме цилиндра с площадью основания, равной единице, и высотой 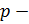плотность газа на высоте . Отсюда

Температура является некоторой функцией от . Если вид функции известен, то уравнение ( полученное подстановкой уравнения в уравнение плотности идеального газа ) можно проинтегрировать найти зависимость Для случая изотермической атмосферы интегрирование приведет к соотношению 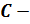константа . Потенцируя полученное выражение и учтя, то, что 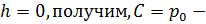давление на высоте Тем самым мы получили барометрическую формулу , из которой следует, что давление убывает с высотой, тем быстрее, чем тяжелее газ (больше М) и чем ниже температура.

Реальные газы. Поправки на объем молекул и внутреннее давление. Уравнение Ван-Дер-Вальса. Изотермы Ван-Дер-Вальса и изотермы реального газа. Критическая изотерма. Сжижение газа. Внутренняя энергия реального газа.

Реальные газы – газы, свойства которых зависят от взаимодействия молекул. В обычных условиях, когда средняя потенциальная энергия межмолекулярного взаимодействия много меньше средней кинетической энергии молекул, свойства реальных и идеальных газов отличаются незначительно. Поведение этих газов резко различно при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона: , где p — давление; V — объем; T — температура; Z_r = Z_r (p,T) — коэффициент сжимаемости газа; m — масса; М — молярная масса; R — газовая постоянная. (для газов с низкой температурой сжижения (He, H₂, Ne и даже N₂, O₂, Ar, CO, CH₄) при давлениях до 50 атм. отклонения не превышают 5 %, а при давлениях до 10 атм. – 2 %. Легко конденсирующиеся газы (CO2, SO₂, Cl₂, CH₃Cl) уже при 1 атм. обнаруживают отклонения до 3 %. ) Ван–дер–Ваальс, объясняя свойства реальных газов и жидкостей, предположил, что на малых расстояниях между молекулами действуют силы отталкивания, которые с увеличением расстояния сменяются силами притяжения. Межмолекулярные взаимодействия имеют электрическую природу и складываются из сил притяжения (ориентационных, индукционных) и сил отталкивания. Поправки на объём молекул и внутреннее давление. В 1873 г. Ван-дер-Ваальс написал свое классическое уравнение. Введенные им поправки в уравнение для идеальных газов, учитывающие внутреннее давление (силы притяжения) и объем молекул (силы отталкивания), предсказали конденсацию молекул в жидкость при определенной плотности вещества. Из-за взаимного притяжения между молекулами газ как бы сжимается большим давлением, чем 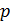, оказываемое на газ стенками сосуда, в котором он заключен. Поправка характеризует ту добавку к внешнему давлению, которая обусловлена взаимным притяжением молекул друг к другу. Заметное взаимодействие молекул друг на друга осуществляется в пределах небольших расстояний, называемых радиусом молекулярного действия. Сила взаимного притяжения двух элементарных объемов, имеющих размеры порядка этого радиуса, пропорциональна как числу молекул, заключенных в одном из объемов, так и числу молекул, заключенных в другом объеме. Каждое из этих чисел в свою очередь пропорционально числу молекул в единице объема, т.е. обратно пропорциональна объему газа. Этими соображениями можно пояснить то обстоятельство, что поправка к давлению в уравнении имеет вид 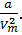Поправка 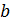характеризует ту часть объема, которая недопустима для движения молекул. Величина поправки равна учетверенному собственному объему всех молекул 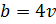, зависит только от химической природы газа (от эффективного диаметра молекул) .
Поправка учитывает наличие сил притяжения между молекулами. На каждую молекулу ударяющуюся о стенку сосуда действует тормозящая сила со стороны соседних молекул (внутри жидкости эти силы взаимно компенсированы), количество которых пропорционально концентрации молекул. таким образом на каждую молекулу действует сила , где 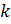- коэффициент пропорциональности зависящий от химической природы газа. Суммарная сила всех молекул, деленная на площадь дает дополнительное давление испытываемое газом , но количество молекул , где R - радиус молекул, а 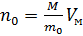, где М - молярная масса газа, - масса молекулы, - молярный объем. Тогда 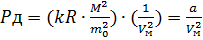, таким образом, 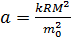как и 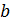зависит только от химической природы газа. Уравнение Ван-дер-Ваальса. Наиболее простым и качественно верно отображающим поведение реального газа, является уравнение Ван-дер-Ваальса: Для одного моля газа Ван-дер-Ваальса оно имеет вид: , где 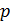— давление, — молярный объём, — абсолютная температура, — универсальная газовая постоянная, член изображающий эффект молекулярных сил взаимодействия. Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка 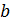— объем молекул газа. Для молей газа Ван-дер-Ваальса уравнение состояния выглядит так: где 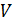— объём константы Ван-дер-Ваальса для 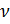молей(где P - давление, v - количество молей газа, V - объем, R - универсальная газовая постоянная, T - абсолютная температура, поправка учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка 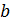— поправка, учитывающая объем молекул газа). Их связь с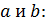 . Уравнение можно переписать так, чтобы выразить в явном виде давление: Чтобы записать уравнение для произвольной массы , нужно учесть, что ν молей газа при тех же условиях занимают в ν раз больший объем: Заменив в через , получим: 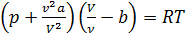Изотермы Ван-дер-Ваальса и изотермы реального газа. Проанализируем изотермы уравнения Ван–дер–Ваальса – зависимости Р от V для реального газа при постоянной температуре. Умножив уравнение Ван-дер-Ваальса на V ² и раскрыв скобки, получаем: PV ³ – ( RT + bP ) vV ² + av ² V - abv ³ = 0. Поскольку данное уравнение имеет третью степень относительно V, а коэффициенты при V действительны, то оно имеет либо один, либо три вещественных корня, т.е. изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках, как это изображено на рисунке 7.4 . Причем с повышением температуры мы перейдем от немонотонной зависимости Р = Р(V) к монотонной однозначной функции. Изотерма при Т_кр, которая разделяет немонотонные T < T_кр и монотонные T > Т_кр изотермы, соответствует изотерме при критической температуре. При температуре выше критической зависимость Р = Р(V) является однозначной монотонной функцией объема. Это означает, что при T > Т_кр вещество находится только в одном, газообразном состоянии, как это имело место у идеального газа. При температуре газа ниже критической такая однозначность исчезает, а это означает возможность перехода вещества из газообразного в жидкое и наоборот. На участке АСВ изотермы Т₁ давление растет с увеличением объема (dP/dV) > 0. Данное состояние неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности. Поэтому область ВСА не может устойчиво существовать. В областях DLB и AGE давление падает с увеличением объема (dP/dV)_Т < 0 – это необходимое, но не достаточное условие устойчивого равновесия. Эксперимент показывает, что система переходит из области устойчивых состояний GE (газ) в область устойчивых состояний LD (жидкость) через двухфазное состояние (газ – жидкость) GL вдоль горизонтальной изотермы GCL. При квазистатическом сжатии, нач иная с точки G, система распадается на 2 фазы – жидкость и газ, причем плотности жидкости и газа остаются при сжатии неизменными и равными их значениям в точках L и G соответственно. При сжатии количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе – увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние. Наличие критической точки на изотерме Ван–дер–Ваальса означает, что для каждой жидкости существует такая температура, выше которой вещество может существовать только в газообразном состоянии. К этому заключению пришел и Д.И. Менделеев в 1861 г. Критическую точку K мы определили как точку перегиба критической изотермы, в которой касательная к изотерме горизонтальна (рис. 7.5). Ее можно определить также как точку, в которую в пределе переходят горизонтальные участки изотерм при повышении температуры до критической. На этом основан способ определения критических параметров P_k, V_k, Т_k. Строится система изотерм при различных температурах. Предельная изотерма, у которой горизонтальный участок LG (рис. 7.4) переходит в точку, будет критической изотермой, а указанная точка – критической точкой (рис. 7.5). Критическая изотерма.

Также существует такое понятие как критическая температура, если газ находится при температуре выше критической (индивидуальна для каждого газа, например для углекислого газа примерно 340 К), то его уже невозможно превратить в жидкость, какое бы давление к нему не прилагалось. Данное явление возникает вследствие того, что при критической температуре силы поверхностного натяжения жидкости равны нулю. Если продолжать медленно сжимать газ при температуре большей критической, то после достижения им объёма, равного приблизительно четырем собственным объёмам молекул, составляющих газ, сжимаемость газа начинает резко падать.

Сжижение газа. Сжиже́ние га́зов включает в себя несколько стадий, необходимых для перевода газа в жидкое состояние. Эти процессы используются для научных, промышленных и коммерческих целей. Все газы могут быть приведены в жидкое состояние путём простого охлаждения при нормальном атмосферном давлении. Однако для некоторых газов достаточно определённого повышения давления (углекислый газ, хлор). Другие (кислород, водород, азот) находятся в баллонах в сжатом состоянии. Дело в том, что газ не может быть сжижен при сколь угодно высоком давлении выше так называемой критической температуры. Первыми были сжижены газы с критической температурой значительно выше комнатной (аммиак, сернистый газ, углекислый газ и пр.), при этом было достаточно одного повышения давления. Уравнение состояния реальных газов Ван-дер-Ваальса показывает, что всякий газ может быть переведен в жидкое состояние, но необходимым условием для этого является предварительное охлаждение газа до температуры ниже критической. Углекислый газ, например, можно сжижить при комнатной температуре, поскольку его критическая температура равна 31,1 °C. То же можно сказать и о таких газах, как аммиак и хлор. Рассмотрим явление адиабатического расширения газа в вакуум. Представим себе сосуд, разделенный на две части перегородкой. В одной части находится газ, в другой - вакуум. Если убрать перегородку, то газ устремится в пустую часть сосуда. Так как работа против внешних сил в рассматриваемом случае отсутствует и, по условию, теплообмена нет, то внутренняя энергия газа до и после расширения газа должна быть одинаковой: 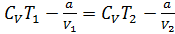. Изменение температуры: 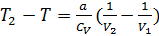Так как V₂>V₁, то Т₂<T₁ (при расширении в пустоту газ Ван-дер-Ваальса охлаждается). Если охлажденной порцией газа охлаждать следующие порции, то можно добиться сжижения газа. Внутренняя энергия реального газа. Для нахождения внутренней энергии воспользуемся тем обстоятельством, что работа, совершаемая при расширении газа против сил взаимного притяжения молекул к друг другу, равна приращению энергии взаимодействия 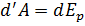. Силы взаимного притяжения между молекулами учтены в уравнении с помощью добавки к давлению, равной . Соответственно работа против сил взаимодействия между молекулами может быть представлена в виде . Таким образом Интегрирование этого выражения дает, что . Внутренняя энергия зависит как от объема, так и от температуры. Следовательно, выражение для имеет вид (константа включена в 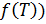. Это выражение в пределе при стремлении объема к бесконечности должно переходить в выражение для внутренней энергии идеального газа. Следовательно, .Итак, внутренняя энергия для одного моля определяется формулой . Внутренняя энергия 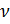молей равна: 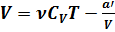(мы учли, что и 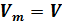). По формулам и 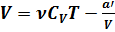можно вычислять приближенные значения внутренней энергии реальных газов.