О рациональной форме поперечного сечения балок при изгибе

 

На рис. 8.21 показана эпюра распределения нормальных напряжений по высоте сечения балки. Учитывая, что напряжения по высоте сечения балки распределены не равномерно, материал, расположенный возле нейтрального слоя нагружен мало. Поэтому в целях экономии и снижения веса конструкции для элементов, работающих на изгиб, следует выбирать такую форму поперечного сечения, чтобы большая часть материала была удалена от нейтральной линии. Таким сечением являются два прямоугольника, расположенные в зоне верхних и нижних волокон балки. Соединив эти два прямоугольника вертикальной полосой, получим так называемое двутавровое сечение.

Изгибающий момент, который безопасно может выдержать поперечное сечение, пропорционально моменту сопротивления W. Расход материала пропорционален площади поперечного сечения F. Следовательно, чем больше величина этого отношения, тем больший изгибающий момент выдержит сечение с заданной площадью F.

β = 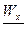 - критерий оценки качества профиля.

 

Касательные напряжения при изгибе балки

 

При поперечном изгибе бруса в сечениях балки действуют изгибающие моменты и поперечные силы. Изгибающие моменты вызывают действие нормальных напряжений, поперечные (перерезывающие) силы – касательные напряжения. В соответствии с законом парности касательных напряжений, последние возникают не только в поперечных, но и в продольных сечениях. При этом происходит сдвиг волокон относительно друг друга, что противоречит гипотезе плоских сечений. Однако, как сказано выше, влияние этого фактора на величину нормальных напряжений не велико. Поэтому нормальные напряжения будем вычислять по приведенной ранее формуле (8.8).

σ_z =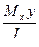

На (рис 8.22а) представлена балка, работающая в условиях поперечного изгиба. Для нахождения касательных напряжений двумя сечениями 1:1 и 2:2 выделим элемент длиной dz и рассмотрим его в равновесии (рис. 8.22в).

 

По грани 1:1 действует изгибающий момент М_1:1=М_х  и поперечная сила Q_1:1=А.

По грани 2:2 действует изгибающий момент М_2:2=М_х+dM_x и поперечная сила Q_2:2=А.

От изгибающего момента М_1:1=М_х по грани 1:1 действуют нормальные напряжения

σ₁ =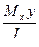

От изгибающего момента М_2:2=М_х+dM_x по грани 2:2 действуют нормальные напряжения

σ₂ =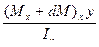

Определим касательные напряжения на уровне y, взятые от оси х. Для этого отсечем параллелепипед авсda₁b₁c₁d₁ и рассмотрим его в равновесии (рис. 8. 22с).

Продольное усилие N₁ является равнодействующей нормальных напряжений, действующих по грани аа₁с₁с. Элементарное усилие, действующее на этой боковой грани элемента

dN₁ = σ₁dF

Подставив сюда значение нормального напряжения, получим

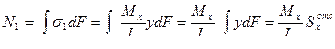                  (а)

Интегрирование ведется по площади отсеченной грани аа₁сс₁. Интеграл в выражении (а) представляет собой статический момент отсеченной части площади относительно нейтральной оси х.

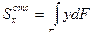
Аналогично можно найти усилие N₂

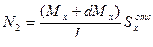                                                                                  (в)

Поперечная сила Q_y  по грани 2:2 приводит к появлению касательных напряжений, которые направлены в сторону поперечной силы, т.е. вниз.

Введем гипотезу о распределении касательных напряжений по ширине сечения балки. Касательные напряжения в балке, на расстоянии у от нейтральной оси, по ширине сечения постоянны и направлены в сторону действия поперечной силы.

На горизонтальной грани рассматриваемого элемента по закону парности касательных напряжений будут возникать такие же напряжения, как и на уровне у боковой грани. Равнодействующую этих касательных напряжений обозначим через dТ.

dT = dFτ = b dz τ                                                 (c)

Записав условия равновесия элемента, получим:

ΣF_z = 0 → N₁ + dT – N₂ = 0

 

В полученное уравнение подставим значения составляющих из выражений (а), (в), (с)

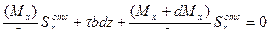
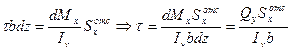
Учитывая, что:

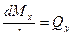
касательные напряжения при изгибе можно найти по формуле (8.11).

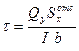                                                                                                                        (8.11)

В формуле (8.11) обозначено:

τ- касательные напряжения в поперечном сечении балки на расстоянии у от нейтрального слоя,

Q_y – поперечная сила в сечении балки, в котором вычисляются касательные напряжения,

S_x^отс – статический момент части площади поперечного сечения относительно нейтральной оси х, расположенный выше или ниже уровня у, где определяются касательные напряжения,

b – ширина сечения балки в том месте по высоте сечения, где определяются касательные напряжения,

I_x – момент инерции всего поперечного сечения относительно оси х.

Формула (8.11) получена русским ученым Журавским и носит его имя.

 

---

Дата добавления: 2018-11-24; просмотров: 499; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!