Лексикографическое расположение членов многочлена
Замечание: Многочлены от одного переменного записывают либо по убывающим степеням переменного, либо по возрастающим степеням.
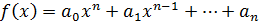

Расположение членов многочлена от n переменных аналогично расположению слов в словарях.
а б в г

 (1)
(1)
 (2)
(2)


…


Определение. Член (1) будет выше члена (2), если  , что
, что  ,
,  , …,
, …,  ,
,  .
.
Понятие «быть выше» является транзитивным, т.е. если первый выше второго, а второй выше третьего, то первый выше третьего.
Любые два члена многочлена можно сравнить по высоте.

Лемма о высшем члене произведения многочленов:
Высший член произведения двух многочленов равен произведению высших членов данных многочленов.
 ;
; 
 - высший член первого многочлена f.
- высший член первого многочлена f.
 – произведение членов многочленов f.
– произведение членов многочленов f.
 - высший член многочлена
- высший член многочлена  .
.
 - произведение членов многочлена
- произведение членов многочлена  .
.
 (1)
(1)
 (2)
(2)
 (3)
(3)
|
|
|
 (4)
(4)
Сравним по высоте (1) и (2).


…




…


Сравним (1) и (3).




Т.к.  - показатель высшего члена,
- показатель высшего члена,  - произведения
- произведения


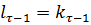
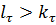
…

Первый член выше 3-го.
Сравним (3) и (4). … (4) ниже чем (3).
По свойству транзитивности (1) выше всех остальных. Ч.т.д.
Пример: Расположить многочлены в лексикографическом смысле и найти высший член произведения.




Высший член  .
.
Симметрические многочлены от n переменных
Среди многочленов от n переменных встречаются такие, которые не зависят от транспозиции(перестановк переменных.
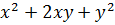


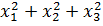 3
3 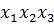

 -3
-3 

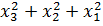 -3
-3 
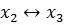
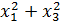 +
+  -3
-3 
Говорят, что переменные в эти многочлены входят симметричным образом, их называют симметрическими многочленами.
|
|
|
Многочлен называется симметрическим, если он не изменяется при любой транспозиции переменных.
Если симметрический многочлен входит 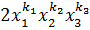 слагаемым, то обязательно в этот многочлен войдут слагаемые
слагаемым, то обязательно в этот многочлен войдут слагаемые  ,
,  … и др.
… и др.
 - симметрический.
- симметрический.
Пример: Дополнить многочлен  до минимального симметрического.
до минимального симметрического.

 – моногенный многочлен.
– моногенный многочлен.
n=4: 
n=3: 
Среди симметрических многочленов существуют простейшие или элементарные многочлены.
n переменных:



… 


n=3:



n=4:
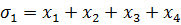



Числа из поля P и 0-ой многочлен являются симметрическими.
Симметрические многочлены являются подмножеством кольца всех многочленов.
Сумма любых двух симметрических многочленов также является симметрическим многочленом; произведение любых двух симметрических многочленов тоже симметрический многочлен.
Во множестве симметрических многочленов выполнимы операции сложения и умножения.
Сложение коммутативно и ассоциативно; существует 0-ой многочлен; -  тоже симметрический; умножение симметрических многочленов дистрибутивно относительно сложения, т.к. это выполняется для всех многочленов.
тоже симметрический; умножение симметрических многочленов дистрибутивно относительно сложения, т.к. это выполняется для всех многочленов.
ð Симметрические многочлены образуют подкольцо кольца всех многочленов.
|
|
|
n=3:




Всякое выражение в виде многочлена от основных симметрических многочленов является симметрическим многочлен от  ,
,  ,
,  .
.
Любой многочлен  после подстановки вместо
после подстановки вместо  их выражают через
их выражают через  обращается в симметрический многочлен.
обращается в симметрический многочлен.
Основная теорема о симметрических многочленах:
Всякий симметрический многочлен от n переменных представим в виде многочлена от основных симметрических многочленов с коэффициентами из того же поля P, что и данный многочлен.
Доказательство:
Пусть дан симметрический многочлен  .
.

 (*)
(*)

… 
Найдем высший член симметрического многочлена  .
.
Докажем вспомогательную лемму:
Показатели в высшем члене симметрического многочлена удовлетворяют цепочке  .
.
Метод «от противного».
Пусть 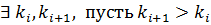 . Тогда т.к. многочлен симметрический, то на ряду со старшим членом
. Тогда т.к. многочлен симметрический, то на ряду со старшим членом  (1) должен быть
(1) должен быть  (2).
(2).
Член (2) будет выше члена (1), что противоречит выбору высшего члена (однозначно) =>  не верно =>
не верно =>



… 
По высшему члену строим  .
.
 (2)
(2)
 в неотрицательных степенях.
в неотрицательных степенях.
|
|
|
Если вместо 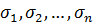 подставим их выражения через
подставим их выражения через  (*) и выполнить все указанные действия, то получим симметрический многочлен, высший член которого будет равен высшему члену
(*) и выполнить все указанные действия, то получим симметрический многочлен, высший член которого будет равен высшему члену  .
.
высший член:


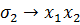

…  …
… 
По лемме высший член произведения равен произведению этих членов.
высший член:


высший член 
 (2) будет ниже члена (1)
(2) будет ниже члена (1)

По высшему члену (2) составим одночлен  .
.
Вместо 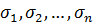 подставим (*) и выполнив все указанные действия получим симметрический многочлен, высший член которого будет равен высшему члену (2).
подставим (*) и выполнив все указанные действия получим симметрический многочлен, высший член которого будет равен высшему члену (2).
 – симметрический.
– симметрический.
Высший член понижен по сравнению со (2)
 ,
,  .
.
Процесс конечен, т.к. показатели конечное число.
Настанет момент  .
.
Складывая правые и левые части равенств
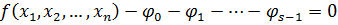

А это многочлен от  .
.
Дата добавления: 2018-11-24; просмотров: 929; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
