Теорема о разложении многочлена в произведении неприводимых над P множителей.
Теорема:
Всякий  , ст.
, ст. 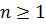 , либо неприводим, либо представим в виде произведения неприводимых множителей:
, либо неприводим, либо представим в виде произведения неприводимых множителей:
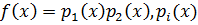 – неприводимый многочлен, (1)
– неприводимый многочлен, (1)
причем представление (1) однозначно с точностью до порядка следования сомножителей и множителей нулевой степени.
1) Существование.
Доказательство: Доказательство существования такого представления проведем методом индукции.
I. 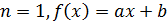 над P неприводим (свойство 1), для многочлена 1-ой степени теорема верна.
над P неприводим (свойство 1), для многочлена 1-ой степени теорема верна.
II. Предположим, что для любого  степени
степени 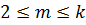 , теорема верна.
, теорема верна.
III. Докажем теорему для многочленов  ст. k+1.
ст. k+1.
Многочлен k+1 степени не является числом, т.к. числами являются только многочлены 0 степени.
Если он неприводим, то теорема верна.
Если приводим: 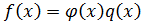
ст. 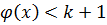
ст. 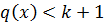
по предположению эти многочлены удовлетворяют условию теоремы
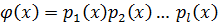
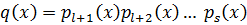
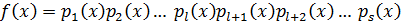
IV. Т.к. А(1) верно и (А(m)) => А(k+1), то на основании принципа мат. индукции это утверждение справедливо для всех многочленов степени n≥1.
2) Единственность.
Разложение многочлена на неприводимые множители однозначно, если:
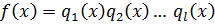 ,
,
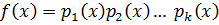 .
.
1) k=l
2) 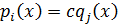
Метод мат. индукции:
I. 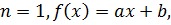 разложение из одного сомножителя. Теорема верна.
разложение из одного сомножителя. Теорема верна.
II. Предположим для любого  ст.
ст. 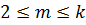 , разложение однозначно с точностью до порядка следования и множителя 0-ой степени.
, разложение однозначно с точностью до порядка следования и множителя 0-ой степени.
III. Докажем единственность разложения для многочленов k+1 степени.
 k+1 степени.
k+1 степени.
|
|
|
Он разлагается на неприводимые множители по первой части теоремы. Пусть разлагается двумя способами:
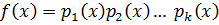 ,
,
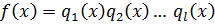 .
.
Надо доказать, что 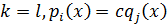 .
.
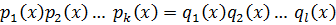
Правая часть  , т.к. левая делится, но это возможно, когда
, т.к. левая делится, но это возможно, когда 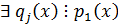 .
.
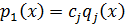
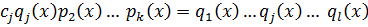
Разделим на 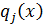 .
.
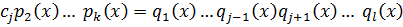
Правая и левая части являются разложением многочлена 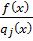 на неприводимый множитель, степень которого ≤ k, а по предположению для таких многочленов теорема справедлива, т.е. разложение однозначно с точностью до порядка следования сомножителей и множителя 0-ой степени, т.е.
на неприводимый множитель, степень которого ≤ k, а по предположению для таких многочленов теорема справедлива, т.е. разложение однозначно с точностью до порядка следования сомножителей и множителя 0-ой степени, т.е.
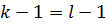 ,
,
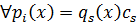 ,
,
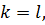
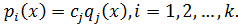
ð Разложение однозначно.
IV. А(1) и А(m), ( 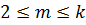 ) => А(k+1) => А(n) – истина,
) => А(k+1) => А(n) – истина, 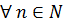 .
.
Замечание: В разложении многочлена 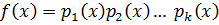 множители могут повторяться несколько раз:
множители могут повторяться несколько раз:
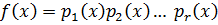 ,
,
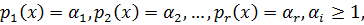
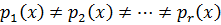 .
.
Если считать, что старший коэффициент у всех неприводимых многочленов 1, то неприводимый многочлен со старшим коэффициентом 1 называется нормированным.
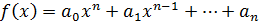 ,
,
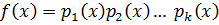 ,
,
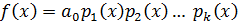 .
.
Последняя формула – это разложение  на нормированные неприводимые множители.
на нормированные неприводимые множители.
Пример: 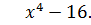
Разложим на неприводимые множители.
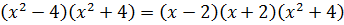 - над R.
- над R.
Над C: 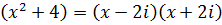 .
.
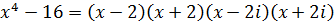 .
.
Неприводимый многочлен 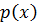 называется k-кратным множителем многочлена
называется k-кратным множителем многочлена  , если
, если 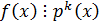 , но не делится
, но не делится 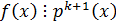 .
.
Производная многочлена.
Теорема о k -кратном множителе.
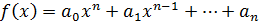 .
.
Первой производной многочлена  называется многочлен вида:
называется многочлен вида:
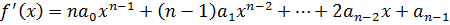 .
.
|
|
|
Второй производной многочлена  называется производная от первой производной многочлена
называется производная от первой производной многочлена  :
:
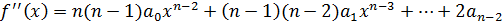 .
.
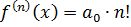
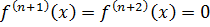
Для многочленов справедливы правила дифференцирования:
1) 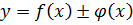 ;
;
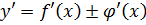 .
.
2) 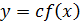 ;
;
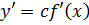 .
.
3) 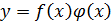 ;
;
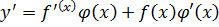 .
.
4) 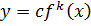 ;
;
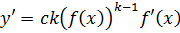 .
.
Теорема о кратном множителе многочлена 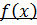 :
:
Если 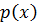 является k-кратным множителем в разложении многочлена
является k-кратным множителем в разложении многочлена  над P, то этот многочлен будет являться множителем (k-1) кратности в разложении его производной
над P, то этот многочлен будет являться множителем (k-1) кратности в разложении его производной 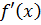 .
.
Доказательство:
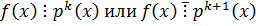
ð 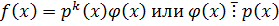
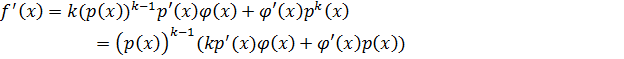
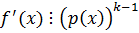
Покажем, что 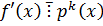 .
.
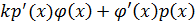
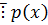
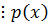
Сумма 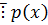 .
.
Многочлен 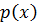 для
для  является (k-1)-кратным.
является (k-1)-кратным.
Теорема о k -кратном корне многочлена 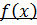 :
:
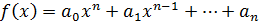 , c – k-кратный корень многочлена
, c – k-кратный корень многочлена  .
.
Всякое число с, являющееся корнем k-кратности многочлена  , является корнем его производной кратности (k-1).
, является корнем его производной кратности (k-1).
Доказательство:
Дано: c – k-кратный корень.
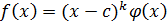
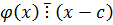
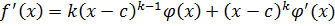
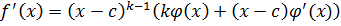
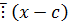
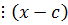
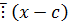
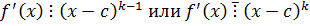
c – корень (k-1) кратности.
Пример: 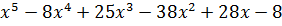 ,
, 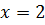
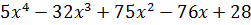
| 5 | -32 | 75 | -76 | 28 | |
| 2 | 5 | -22 | 31 | -14 | 0 |
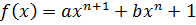 .
.
с=1 – корень.
Следствие:
1) 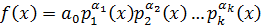
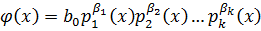
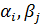 - могут быть нулями.
- могут быть нулями.
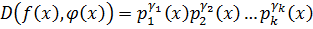 .
.
Произведение всех общих множителей, входящих в разложение каждого из них:
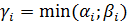 .
.
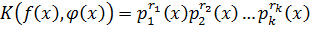 ,
,
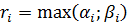
произведение неприводимых множителей, входящих в разложение хотя бы одного.
|
|
|
Учитывая теорему о k-кратном множителе многочлена  можно доказать следующую теорему.
можно доказать следующую теорему.
2) Многочлен  не имеет кратных множителей ó
не имеет кратных множителей ó 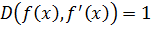 .
.
Доказательство:
Пусть дан многочлен 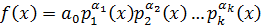 .
.
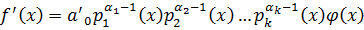 .
.
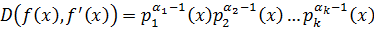 .
.
Дано: многочлен 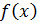 не имеет кратных множителей.
не имеет кратных множителей.
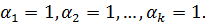
В произведение будут входить в 0-ой степени.
Тогда 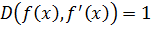 .
.
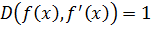 . => Значит каждый
. => Значит каждый 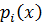 в разложение
в разложение 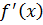 входит в 0-ой степени, значит, в сам многочлен он войдет в 1 степени.
входит в 0-ой степени, значит, в сам многочлен он войдет в 1 степени.
Пример: 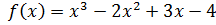
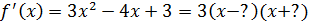
Есть ли кратные неприводимые множители?
D<0. Найти НОД.
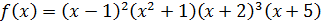
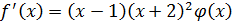
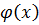 - 4-ой степени.
- 4-ой степени.
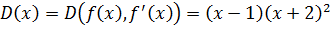 .
.
Дата добавления: 2018-11-24; просмотров: 931; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
