Многочлены над полем рациональных чисел
Многочлен вида
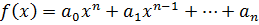 ,
, 
называется примитивным, если его коэффициенты взаимно простые числа
 .
.
Например:  - примитивный.
- примитивный.
Теорема: Всякий многочлен с рациональными коэффициентами можно представить в виде произведения несократимой дроби на примитивный многочлен.
Доказательство:
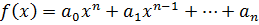 ,
,  .
.
 .
.
 .
.
Найдется  - общий знаменатель.
- общий знаменатель.
По свойству дробей все коэффициенты можно привести к общему знаменателю  .
.
 .
.
 .
.
 - примитивный многочлен.
- примитивный многочлен.
Если  – несократимая, то теорема доказана.
– несократимая, то теорема доказана.
Если  - сократимая, то
- сократимая, то  ,
, 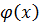 – примитивный.
– примитивный.
 . Ч.т.д.
. Ч.т.д.
Например:  .
.
 .
.
Лемма Гаусса: Произведение примитивных многочленов является примитивным.
Доказательство:
 .
.
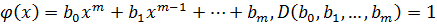 .
.
 .
.
 .
.
Предположим, что этот многочлен не примитивный. Тогда  .
.
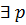 - простое число, на которое все коэффициенты делятся.
- простое число, на которое все коэффициенты делятся.
 .
.

Т.к. многочлены  являются примитивными, то все коэффициенты и первого, и второго многочлена делиться на p не могут.
являются примитивными, то все коэффициенты и первого, и второго многочлена делиться на p не могут.
Пусть  .
.
 .
.
 .
.
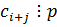 по условию все слагаемые, кроме одного делятся на p. Тогда
по условию все слагаемые, кроме одного делятся на p. Тогда  , отсюда
, отсюда  или
или  , а это противоречит выбору коэффициентов
, а это противоречит выбору коэффициентов  . Противоречие в результате неверного предположения. Значит
. Противоречие в результате неверного предположения. Значит  . Значит многочлены
. Значит многочлены 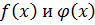 – примитивные.
– примитивные.
Сведение вопроса о приводимости многочленов над полем рациональных числе к вопросу о приводимости этих многочленов над кольцом целых чисел.
Пусть многочлен 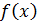 с рациональными коэффициентами. Тогда его можно представить как
с рациональными коэффициентами. Тогда его можно представить как  ,
, 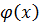 – примитивный,
– примитивный,  – несократимая дробь.
– несократимая дробь.
|
|
|
Если 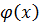 с целыми коэффициентами будет приводим над Z:
с целыми коэффициентами будет приводим над Z:
 ,
,  с целыми коэффициентами, ст.
с целыми коэффициентами, ст.  , ст.
, ст.  ,
,
тогда  ,
, 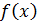 - приводим.
- приводим.
Пусть 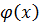 приводим над Q. Тогда покажем, что он приводим над кольцом Z.
приводим над Q. Тогда покажем, что он приводим над кольцом Z.
Пусть  с рациональными коэффициентами.
с рациональными коэффициентами.
Тогда 
 .
.
Тогда  .
.
По лемме Гаусса  – примитивные его коэффициенты целого и взаимно простые,
– примитивные его коэффициенты целого и взаимно простые, 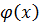 - примитивный с целыми и взаимно простыми коэффициентами.
- примитивный с целыми и взаимно простыми коэффициентами.
Тогда  .
.
Произведение примитивно умноженного на  даст нам многочлен с целыми коэффициентами ó
даст нам многочлен с целыми коэффициентами ó  .
.
А значит  .
.
Т.к. 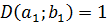 , то
, то  ,
, 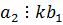 .
.
Т.к.  , то
, то  .
.
Получили  .
.
Разложили 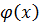 ,
, 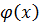 приводим над Z. Значит
приводим над Z. Значит 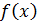 будет приводим над Q.
будет приводим над Q.
Вопрос о приводимости многочлена над Q сводится к вопросу о приводимости над Z.
Критерий Эйзенштейна о неприводимости многочленов над полем рациональных чисел
Если вопрос о приводимости и неприводимости многочленов над полем C и R решается легко, то вопрос о приводимости и неприводимости многочленов над полем Q решается довольно сложно.
Существует несколько достаточных критериев приводимости и неприводимости многочленов и несколько необходимых. Мы рассмотрим наиболее важные.
Если многочлен 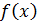 с целыми коэффициентами имеет рациональный корень
с целыми коэффициентами имеет рациональный корень  , то он приводим над Q
, то он приводим над Q 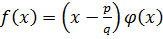 .
.
|
|
|
Докажем критерий Эйзенштейна (достаточное условие того, чтобы многочлен с целыми коэффициентами был неприводим над Q).
Многочлен 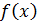 с целыми коэффициентами
с целыми коэффициентами
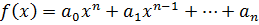 ,
, 
будет неприводим над Q, если существует простое число p, удовлетворяющее условиям:
1) 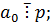
2) 
3)  .
.
Доказательство:
Пусть 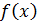 удовлетворяет всем условиям критерия и пусть он приводим =>
удовлетворяет всем условиям критерия и пусть он приводим =>  .
.
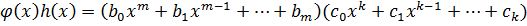 , где
, где  .
.
Тогда

Все коэффициенты, кроме 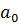 делятся на p, когда
делятся на p, когда 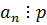 , но
, но  ,
,  .
.
Пусть  (если бы
(если бы  , то
, то 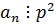 , а у нас
, а у нас  , значит
, значит  ).
).
 , тогда
, тогда  , но
, но  =>
=>  .
.
 , тогда
, тогда  =>
=>  .
.
На m-ом шаге получим  . Поднимемся в первое равенство:
. Поднимемся в первое равенство:
 =>
=>  , а это против условия (1) критерия Эйзенштейна.
, а это против условия (1) критерия Эйзенштейна.
Значит многочлен неприводим.
Пример: Выяснить приводимость многочлена 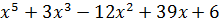 существует 3:
существует 3:  .
.
0,3,-12,39,6  3. Значит многочлен неприводим над Q.
3. Значит многочлен неприводим над Q.
Из критерия Эйзенштейна следует, что над полем Q существует неприводимый многочлен сколь угодно большой степени. Докажем, что существует многочлен тысячной степени.
 .
.
2  5;
5;
0,…,0,5,10  .
.
10  25.
25.
Значит многочлен неприводимый над полем Q.
Критерия Эйзенштейна является лишь достаточным условием, поэтому если хотя бы одно из условий критерия не выполняется, то о многочлене нельзя сказать приводимый он или неприводимый.
Дата добавления: 2018-11-24; просмотров: 2990; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
