Кольцо многочленов от n -переменных
Пусть P – произвольное числовое поле.
x1, x2, …, xn – переменные.
Выражение вида 
(1), где 
называется одночленом от n переменных, a – коэффициент одночлена.
Конечная сумма одночленов от n переменных называется многочленом от n переменных.
Степенью одночлена (1) относительно всех переменных называется число равное сумме показателей ( 
).
Каждый член многочлена имеет свою степень.
Степенью многочлена от n переменных относительно всех переменных называется наибольшая из степеней членов данного многочлена.
Множество всех многочленов от n переменных 
.
Теорема: Множество всех многочленов от n переменных над полем P является кольцом.
Введем операцию сложения.
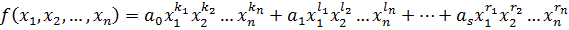. (1)
. (2)
Два одночлена называются подобными, если они различаются только числовым коэффициентом.
В записи (1) и (2) многочлена не должно быть подобных.
Суммой двух многочленов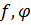 
назовем новый многочлен, который получается при приписывании членам первого многочлена всех членов второго многочлена с теми же знаками.
Из определения суммы двух многочленов следует, что сложение многочленов коммутативно и ассоциативно.
Роль нуля при сложении многочленов играет нулевой многочлен 
.
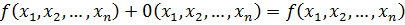
Для любого многочлена существует ему противоположный.
По сложению многочлены образуют абелеву группу.
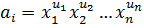
Произведением двух одночленов назовем выражение вида
Произведение двух многочленов от n переменных называется новый многочлен, который получается в результате последовательного перемножения всех членов первого на все члены второго многочлена и приведения подобных одночленов.
|
|
|
Нетрудно доказать, что умножение многочленов дистрибутивно относительно сложения.
Мы доказали, что множество всех многочленов является кольцом (коммутативное, ассоциативное, 0-ой элемент, 
противоположный, умножение дистрибутивно).
Кольцо коммутативно-ассоциативное с 1.
– многочлен нулевой степени
.
Однородные многочлены. Степень произведения многочленов
Многочлен от n переменных 
называется однородным, если все его члены имеют одинаковую степень.
Однородные многочлены называют формой m-ой степени.
однородный многочлен 2-ой степени.
Теорема: Всякий многочлен от n переменных можно представить в виде суммы нескольких однородных многочленов.
Доказательство:
найдем наибольшую степень одночлена, членов имеющих наибольшую степень может оказаться несколько.
Соберем все члены, имеющие наибольшую степень.
Из оставшихся многочленов выберем одночлен, имеющий наибольшую одинаковую степень. И т.д.
;
;
… 
.
.
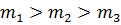Мы записали многочлен в виде суммы одночленов.
Теорема: Степень произведения двух многочленов равна сумме степеней сомножителей.
|
|
|
Доказательство:
, 
.
Ст. f=m.
Ст. h=k.
Ст. f·h=m+k.
Многочлены f и h представим в виде суммы однородных многочленов.
Ст. 
.
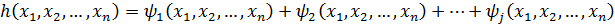
Ст. 
.
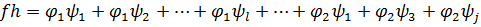
Однородный многочлен ст. 
, s+t.
В произведении f·h все слагаемые будут однородными одночленами, причем ст. 
, а степени всех остальных слагаемых <m+k.
Ст. f·h=m+k.
Если f и h ненулевые, то их произведение ненулевым многочленом не будет.
Кольцо многочленов не содержит делителей нуля.
Дата добавления: 2018-11-24; просмотров: 557; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!