Взаимно-простые многочлены и их свойства.
Определение. 
, тогда 
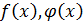– взаимно-простые.
Теорема 1 (критерий):
, 
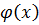взаимно-простые ó 
над P 
.
Доказательство:
1. Необходимость этого условия вытекает из теоремы о линейном представлении НОД.
2. Достаточность.
Дано: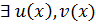 
Доказать: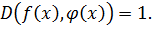 
Метод «от противного».
Пусть 
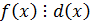
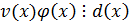
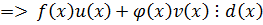
1 
Теорема 2:
и , то 
.
Доказательство:
Т.к. 
по теореме 1
| 
, 
.
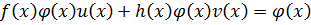
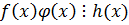Теорема 3:
, то
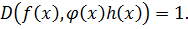
Доказательство:
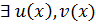Из что над P
Если бы 
, то
общий делитель 
,
а по условию - противоречие =>
.
Теорема 4:
Если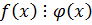 
и 
и 
, то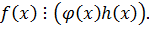 
Доказательство:
, 
.
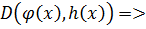
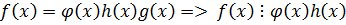Наименьшее общее кратное двух и нескольких многочленов.
Многочлен 
называется общим кратным многочленов 
, если 
, 
КОН двух или нескольких многочленов называется такой многочлен m(x) над P, который является общим кратным: 1) 
; 2) 
; 
- общее кратное.
Теорема:
Для любых двух отличных от нуля многочленов существует НОК.
Теорема:
Если 
, 
, то 
является НОК этих многочленов, 
.
Доказательство:
Т.к. 
- общее кратное.
общее кратное
По теореме 2: 
k, q – взаимно простые.
.
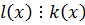
Теорема:
Если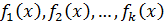 
– многочлены над полем P и 
, 
, …, 
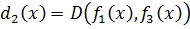, то 
.
|
|
|
Теорема:
Если 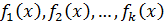– многочлены над полем P и 
, 
, 
, …, 
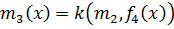, то 
.
Значение многочлена от числа. Корни многочлена.
Деление многочлена на линейный двучлен.
Схема Горнера.
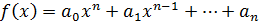над P.
Пусть c – любое число из P.
– число из P.
Это число называется значением многочлена при 
.
Пример: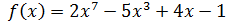 
Определение. Число c называется корнем многочлена , если 
1 – корень многочлена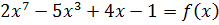 
.
, 
,
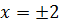, 2i, -2i,
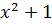, I, -i.
Замечание: Если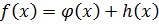 
, то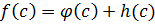 
.
Деление многочлена на линейный двучлен
ax+b, a≠0
По теореме о делении с остатком:
для 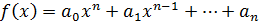над P найдется 
, 
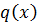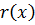
ст. 
ст. 
ст.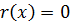 
или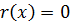
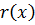– число из P.
В правой части этого равенства раскроем скобки и сгруппируем по степеням x.
Из равенства многочленов получим равенство их коэффициентов.
| 
| 
| … | 
| 
| |
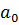
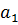
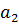
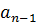
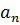
| c | 
| 
| 
| … | 
| r= 
|
Пример:
| 1 | 0 | 2 | 0 | 0 | 0 | 3 | -7 | |
| 2 | 1 | 2 | 6 | 12 | 24 | 48 | 99 | 191 |
Теорема Безу. Следствие из теоремы Безу.
Теорема:
Остаток от деления многочлена на линейный двучлен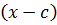 
равен значению многочлена при .
|
|
|
Доказательство:
т. к. делиться на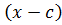 
, то остаток от деления является числом 
не зависящим от x
Следствие (критерий того, чтобы многочлен имел корень):
Число 
является корнем многочлена 
.
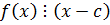Доказательство:
1. Необходимость:
Дано: c – корень .
Доказать: .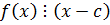
(т.к. c – корень).
По теореме Безу 
.
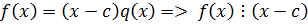
2. Достаточность:
Дано: .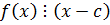
Доказать: c – корень .
(т.к. ).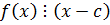
.
Замечание:
По схеме Горнера можно решать следующие задачи:
1) Найти частное и остаток от деления многочлена на линейный двучлен.
2) Находить значение многочлена при любом .
3) Определять является ли число c корнем многочлена.
Нахождение коней многочлена равносильно нахождению его линейных делителей вида 
.
Кратные корни. Теорема о числе корней многочлена 
n – степени.
Число c называется k – кратным корнем , если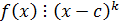 
, но не делится на 
.
Кратность корня многочлена можно определять с помощью схемы Горнера.
Пример: Определить кратность корня 
| 1 | 7 | 16 | 8 | -16 | -16 | |
| -2 | 1 | 5 | 6 | -4 | -8 | 0 |
-2 – корень.
| -2 | 1 | 3 | 0 | -4 | 0 |
| -2 | 1 | 1 | -2 | 0 |
| -2 | 1 | -1 | 0 |
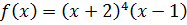
| -2 | 1 | -3 |
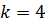
Теорема:
Если имеет степень n, то число корней этого многочлена, принадлежащих полю P, не превосходит n.
|
|
|
Доказательство:
Пусть 
– корень .
По следствию из теоремы Безу:
Если 
не имеет корней над P, то имеет 1 корень.
Пусть 
- корень .
– корень , т.к.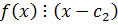 
Если 
продолжим рассуждения.
Пусть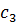 
– корень 
.
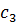– корень .
m – корень.
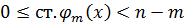
Если бы 
, то в правой части ст. больше m, получим противоречие. Следовательно, 
.
Следствие: Нулевой многочлен над любым полем имеет бесконечно много корней.
Дата добавления: 2018-11-24; просмотров: 2052; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!