Формулы Виета и теорема Виета
Запишем уравнение n-ой степени.
Уравнением n-ой степени называется равенство 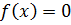 , где
, где  - многочлен n-ой степени, если ставится задача найти такие значения переменной x, при которых это равенство обращается в верное, число c при этом называется корнем уравнения
- многочлен n-ой степени, если ставится задача найти такие значения переменной x, при которых это равенство обращается в верное, число c при этом называется корнем уравнения
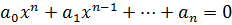 . (1)
. (1)
Корни уравнения это есть корни многочлена  .
.
Мы знаем, что над полем C всякий многочлен n-ой степени имеет n корней.
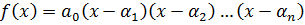 .
.
Формулы Виета выражают связь между корнями уравнения (1) и его коэффициентами.
Возьмем многочлен  со старшим коэффициентом (1) над полем C, он имеет n корней, считая их кратность.
со старшим коэффициентом (1) над полем C, он имеет n корней, считая их кратность.
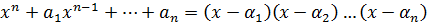 .
.
Раскрывая скобки в правой части этого равенства мы получим:
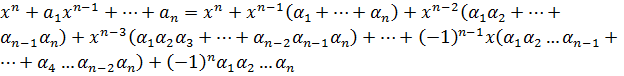 .
.
Формулы Виета:
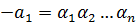 .
.
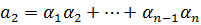 .
.
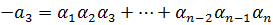 .
.
…
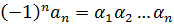 .
.
Если 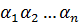 - корни многочлена
- корни многочлена  со старшим коэффициентом 1, то сумма корней взятых по одному равняется вторым коэффициентом многочлена взятых с противоположным знаком. Сумма произведение корней взятых по два равна третьему коэффициенту, сумма произведение взятых по три равна четвертому коэффициенту, …, произведение всех корней равно свободному члену на
со старшим коэффициентом 1, то сумма корней взятых по одному равняется вторым коэффициентом многочлена взятых с противоположным знаком. Сумма произведение корней взятых по два равна третьему коэффициенту, сумма произведение взятых по три равна четвертому коэффициенту, …, произведение всех корней равно свободному члену на 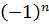 .
.
Уравнения третьей степени с действительными коэффициентами
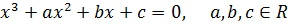 .
.
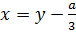 .
.
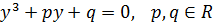 . (2)
. (2)
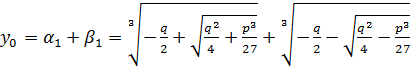 .
.
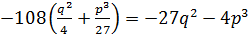 –называется дискриминантом кубического уравнения (2).
–называется дискриминантом кубического уравнения (2).
1) D<0 => 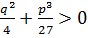 .
.
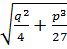 - положительное действительное число.
- положительное действительное число.
|
|
|
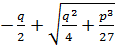 - действительное число.
- действительное число.
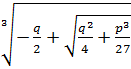 .
.
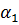 – действительное,
– действительное, 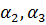 - комплексно-сопряженные.
- комплексно-сопряженные.
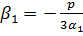 – действительное,
– действительное, 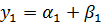 – действительное.
– действительное.
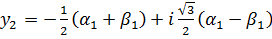 .
.
Один действительный корень и два комплексно-сопряженных.
2) D=0 => 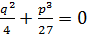 .
.
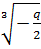 - действительное число.
- действительное число.
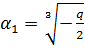 ,
, 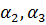 - комплексно-сопряженные.
- комплексно-сопряженные.
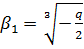 .
.
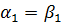 .
.
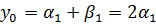 .
.
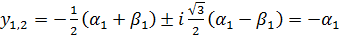 .
.
Все три корня действительные числа.
3) D>0 => 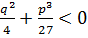 .
.
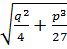 – линейное число.
– линейное число.
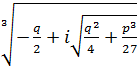 - комплексное число.
- комплексное число.
Корень третьей степени отличается от действительного. Действительным быть не может.
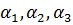 – комплексные числа.
– комплексные числа.
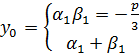 – действительные корни <=> когда числа являются комплексно-сопряженными
– действительные корни <=> когда числа являются комплексно-сопряженными 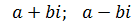 .
.
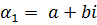 ;
;
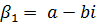 .
.
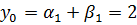 .
.
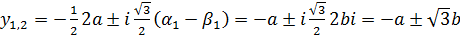 .
.
Все три корня действительные числа.
Корни кубического уравнения часто находят приближенным методом.
Решение уравнений с рациональными коэффициентами. Нахождение рациональных корней уравнения.
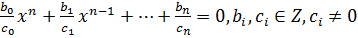 . (1)
. (1)
Если умножить на общий знаменатель 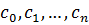 , то получим уравнение с целыми коэффициентами
, то получим уравнение с целыми коэффициентами
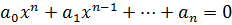 . (2)
. (2)
Если α – корень 1 => α - корень 2.
Если α – корень 2 => α - корень 1.
Сведется к нахождению корней уравнения с целыми коэффициентами.
Теорема 1: Если несократимая дробь  является корнем уравнения
является корнем уравнения 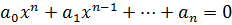 (2),
(2), 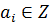 , то числитель дроби – p является делителем свободного члена an, а q является положительным делителем старшего коэффициента.
, то числитель дроби – p является делителем свободного члена an, а q является положительным делителем старшего коэффициента.
|
|
|
Доказательство:
Дано:  - корень уравнения (2) =>
- корень уравнения (2) => 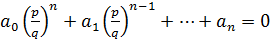 - верное равенство. Умножим его на qn.
- верное равенство. Умножим его на qn.
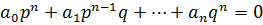
Все слагаемые от 1-го до предпоследнего делятся на p; сумма делится на p => последнее слагаемое делится нацело на p - 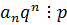 .
.
Все слагаемые, кроме 1-го, делятся на q и сумма делится нацело на q => 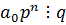 .
.
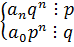
Т.к. p, q – взаимно-простые, то любая степень q с числом p взаимно-простые и наоборот.
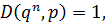
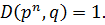
По теореме о взаимно-простых числах (если произведение на число, а один из сомножителей взаимно-простое с этим числом => второе слагаемое делится нацело на p)
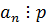
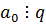
p – делитель свободного члена,
q – делитель старшего коэффициента.
Учитывая 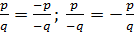 , знаменатель можно брать положительный.
, знаменатель можно брать положительный.
Следствие 1: 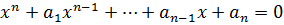 . Если старший коэффициент равен 1, то его корнями могут быть только целые числа, являющиеся делителями свободного числа.
. Если старший коэффициент равен 1, то его корнями могут быть только целые числа, являющиеся делителями свободного числа.
Доказательство:
Если  является корнем уравнения, то по предшествующей теореме q – делитель старшего коэффициента, q – делитель 1.
является корнем уравнения, то по предшествующей теореме q – делитель старшего коэффициента, q – делитель 1.
Значит делитель будет p – делитель свободного члена.
Следствие 2: Целыми корнями уравнения 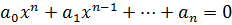 могут быть делители свободного члена.
могут быть делители свободного члена.
|
|
|
Доказательство:
По теореме, если  – корень уравнения (2), то p является делителем свободного члена; q – положительный делитель старшего коэффициента.
– корень уравнения (2), то p является делителем свободного члена; q – положительный делитель старшего коэффициента.
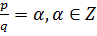 только тогда, когда p=α, q=1 => α является делителем свободного члена.
только тогда, когда p=α, q=1 => α является делителем свободного члена.
Теорема является необходимым условием того, чтобы рациональное число было корнем многочлена с целыми коэффициентами.
1-е необходимое условие существования рационального корня у многочлена с целыми коэффициентами:
Для того чтобы несократимая дробь  была корнем уравнения (2) с целыми коэффициентами необходимо, чтобы числитель этой дроби был делителем свободного члена, а знаменатель – положительным делителем старшего коэффициента.
была корнем уравнения (2) с целыми коэффициентами необходимо, чтобы числитель этой дроби был делителем свободного члена, а знаменатель – положительным делителем старшего коэффициента.
Пример: 3x4+5x3+x2+5x-2=0
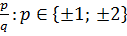 - делители.
- делители.
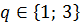
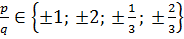 эти числа могут быть рациональными корнями.
эти числа могут быть рациональными корнями.
| 3 | 5 | 1 | 5 | -2 | |
| -2 | 3 | -1 | 3 | -1 | 0 |
| 1/3 | 3 | 0 | 3 | 0 |
-2; 1/3.
Замечание: Если дробей вида  будет много, то существует второе необходимое условие.
будет много, то существует второе необходимое условие.
Теорема 2: Если  – несократимая дробь является корнем уравнения (2) с целыми коэффициентами
– несократимая дробь является корнем уравнения (2) с целыми коэффициентами 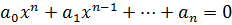 ,
, 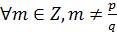 , то
, то 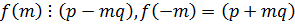 .
.
Доказательство:
Дано:  - корень.
- корень.
Тогда по критерию существования корня
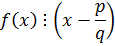
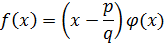
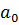
| 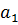
| 
| … | 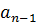
| 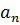
| |

| 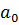
| 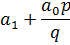
| 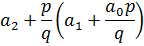
| … | ||
| q0 | q1 | q2 |
Найдем коэффициенты частного.
|
|
|
Коэффициенты частного 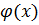 будут дроби со знаменателями q0, q1, …, qn-1.
будут дроби со знаменателями q0, q1, …, qn-1.
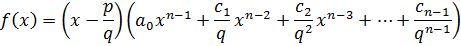
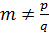 ,
,
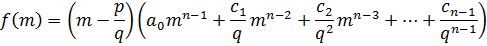
Обе части умножим на qn.
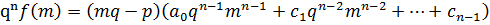
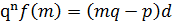
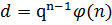 – целое число.
– целое число.
Т.к. 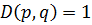 , то
, то 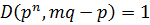 .
.
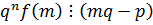 .
.
ð 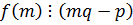 =>
=> 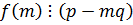 .
.
Если вместо m подставить –m, то аналогично получим 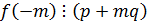 . Ч.т.д.
. Ч.т.д.
2-е необходимое условие:
Для того чтобы несократимая дробь  являлась корнем многочлена с целыми коэффициентами необходимо, чтобы
являлась корнем многочлена с целыми коэффициентами необходимо, чтобы 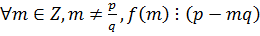 ,
, 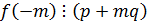 .
.
Замечание: На практике в качестве m берут ±1.
Пример: Найти рациональные корни многочлена.
3x5+17x4+36x3+38x 2+19x+5
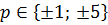 .
.
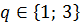 .
.
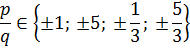
f(1)=118
f(-1)=0
| p | -5 | -1 | -5 |
| q | 1 | 3 | 3 |
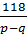 .
.
| 3 | 17 | 36 | 38 | 19 | 5 | |
| -1 | 3 | 14 | 22 | 16 | ||
| -1/3 | 3 | 116 | ||||
| -5/3 | 3 | 12 | 16 |
Рациональных корней нет.
Многочлены от n- переменных
Дата добавления: 2018-11-24; просмотров: 592; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
