Задание № 14. Стереометрия с доказательством.
1. В кубе ABCDA 1 B 1 C 1 D 1 все рёбра равны 5. На его ребре BB 1 отмечена точка K так, что KB=4. Через точки K и C 1 проведена плоскость α, параллельная прямой BD 1 .
а) Докажите, что A 1 P:PB 1=3:1, где P — точка пересечения плоскости α с ребром A 1 B 1 .
б) Найдите угол наклона плоскости α к плоскости грани BB 1 C 1 C.
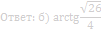
2. В кубе ABCDA 1 B 1 C 1 D 1 все рёбра равны 5. На его ребре BB 1 отмечена точка K так, что KB=4. Через точки K и C 1 проведена плоскость α, параллельная прямой BD 1 .
а) Докажите, что A 1 P:PB 1=3:1, где P — точка пересечения плоскости α с ребром A 1 B 1 .
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.
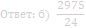
3. Сечением прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью α, содержащей прямую BD 1 и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD— квадрат.
б) Найдите угол между плоскостями α и BCC 1, если AA 1=10, AB=12.
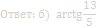
4. В правильной треугольной пирамиде SABC сторона основания AB=6, а боковое ребро SA=4. Точки M иN — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Ответ: б) 8 + 2√2
5. В правильной треугольной пирамиде SABC сторона основания AB=60, а боковое ребро SA=37. ТочкиM и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите расстояние от вершины A до плоскости α.
Ответ: б) 5√3
|
|
|
6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамидыSABC плоскостью α.
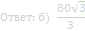
7. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 иBC=6. Длины боковых рёбер пирамиды SA=3, SB=5, SD=3√5.
а) Докажите, что SA— высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
Ответ: б) 2,4
8. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 иBC=6. Длины боковых рёбер пирамиды SA=√21, SB=√85, SD=√57.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.
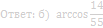
9. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=5 и диагональю BD=9. Все боковые рёбра пирамиды равны 5.На диагонали BD основания ABCD отмечена точка E, а на ребреAS — точка F так, что SF=BE=4.
а) Докажите, что плоскость CEF параллельна ребру SB.
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.
|
|
|
10. В правильной треугольной призме ABCA 1 B 1 C 1 сторона основания AB равна 6, а боковое ребро AA 1равно 2√2. На рёбрах AB, A 1 B 1 и B 1 C 1 отмечены точки M, N и K соответственно, причём AM = B 1 N= C 1 K=2.
а) Пусть L — точка пересечения плоскости MNK с ребром AC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Ответ: б) 15
11. В правильной треугольной призме ABCA 1 B 1 C 1 сторона AB основания равна 6, а боковое ребро AA 1 =3. На ребре AB отмечена точка K так, что AK=1. Точки M и L— середины рёбер A 1 C 1 и B 1 C 1соответственно. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) 3/4
12. В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 сторона AB основания равна 8, а боковое ребро AA 1 равно 4√2. На рёбрах BC и C 1 D 1 отмечены точки K и L соответственно, причём BK= C 1 L=2.Плоскость γ параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A 1 C перпендикулярна плоскости γ.
б) Найдите расстояние от точки B до плоскости γ.
|
|
|
13. В основании прямой треугольной призмы ABCA 1 B 1 C 1 лежит равнобедренный (AB=BC) треугольникABC. Точка K— середина ребра A 1 B 1, а точка M делит ребро AC в отношении AM:MC=1:3.
а) Докажите, что KM ⊥ AC.
б) Найдите угол между прямой KM и плоскостью ABB 1, если AB=6, AC=8 и AA 1= 3.
14. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известны длины рёбер: AB=2√2, AD=6, AA 1=10. На рёбрах AA 1 и BB 1 отмечены точки E и F соответственно, причём A 1 E:EA =3:2 и B 1 F:FB=3:7. Точка T— середина ребра B 1 C 1 .
а) Докажите, что плоскость EFT проходит через точку D 1 .
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Ответ: б) 22,5
15. На ребре AA 1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 взята точка E так, что A 1 E:EA=1:2, на ребре BB 1 — точка F так, что B 1 F:FB=1:5 , а точка Т — середина ребра B 1 C 1 . Известно, что AB=2, AD=6,AA 1=6.
а) Докажите, что плоскость EFT проходит через вершину D 1 .
б) Найдите угол между плоскостью EFT и плоскостью AA 1 B 1 .
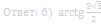
16. На ребрах CD и BB 1 куба ABCDA 1 B 1 C 1 D 1 c ребром 12 отмечены точки Р и Q соответственно, причемDP=4, а B 1 Q=3. Плоскость APQ пересекает ребро CC 1 в точке М.
а) Докажите, что точка М является серединой ребра CC 1 .
б) Найдите расстояние от точки С до плоскости APQ.
|
|
|

17. В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM=DN=4 и АК=3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки К до плоскости SBC.
18. В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а высота равна 1. На ребрах АВ, АС и AS отмечены точки М, N и К соответственно, причем АМ=AN=3 и AK=7/4.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.
19. Основанием прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 является квадрат ABCD со стороной 4, высота призмы равна 6. Точка K делит ребро AA 1 в соотношении AK:KA 1=1:2. Через точки K и Bпроведена плоскость α, параллельная прямой AC и пересекающая реброDD 1 в точке M.
а) Докажите, что плоскость α делит ребро DD 1 в отношении DM:MD 1=2:1.
б) Найдите площадь сечения.
Ответ: б) 8√6
20. В правильной треугольной призме ABCA 1 B 1 C 1 сторона AB основания равна 12, а боковое ребро AA 1равно 3√6. На ребрах AB и B 1 C 1 отмечены точки K и L соответственно, причем AK=2, B 1 L=4. Точка Mсередина A 1 C 1. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) √2
21. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=√5 иBC=2. Длины боковых рёбер пирамиды SA=√7, SB=2√3, SD=√11.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
Ответ: б) 30
22. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA=PQ=RC=2.
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Ответ: б) 7/2
23. В треугольной пирамиде PABC с основанием ABC известно, что AB=13, PB=15, cos PBA=48/65. Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Ответ: б) 90
24. Основанием прямой треугольной призмы ABCA 1 B 1 C 1 является прямоугольный треугольник ABC с прямым углом C. Прямые CA 1 и AB 1 перпендикулярны.
а) Докажите, что AA 1 =AC.
б) Найдите расстояние между прямыми CA 1 и AB 1, если AC = 6, BC = 3.
Ответ: б) √2
25. Дана четырёхугольная пирамида SABCD с прямоугольником ABCD в основании. Сторона AB равна 4, а BC равна 4√2. Высота пирамиды проектируется в центр пересечения диагоналей прямоугольника. Из вершины A и C на ребро SB опущены перпендикуляры AP и CQ.
а) Докажите, что точка P является серединой отрезка BQ.
б) Найдите угол между плоскостями SBA и SBC, если ребро SD равно 8.
26. Дана пирамида PABCD, в основании — трапеция ABCD с большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K.
а) Доказать, что плоскость PAB перпендикулярна плоскости PCD.
б) Найдите объём PKBC, если AB = BC = CD = 2, а высота равна 12.
Ответ: б) 4
27. SABCD — правильная пирамида с вершиной S. Точка M расположена на SD так, что SM : SD = 2 : 3. P— середина ребра AD, а Q середина ребра BC.
а) Доказать, что сечение пирамиды плоскостью MQP — равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость MQP разбивает пирамиду.
Ответ: б) 2/7
28. В треугольной пирамиде SABC известны боковые рёбра SA=SB=7, SC=5. Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
Ответ: б) 16√6
29. На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причёмAM:BM = CN:NB = 1:2. Точки P и Q — середины сторон DA и DC соответственно.
а) Докажите, что P, Q, M и N лежат в плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
Ответ: б) 13/23
30. В основании прямой треугольной призмы ABCA 1 B 1 C 1 лежит прямоугольный треугольник ABC с прямым углом C, AC = 4, BC = 16, AA1=4√2. Точка Q — середина ребра A 1 B 1, а точка P делит ребро B 1 C 1в отношении 1 : 2, считая от вершины C 1. Плоскость APQ пересекает ребро CC 1 в точке M.
а) Докажите, что точка M является серединой ребра CC 1 .
б) Найдите расстояние от точки A 1 до плоскости APQ.
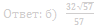
31. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известны длины рёбер: AB = 4, BC = 3, AA 1 = 2. Точки P и Q — середины рёбер A 1 B 1 и CC 1 соответственно. Плоскость APQ пересекает ребро B 1 C 1 в точке U.
а) Докажите, что B 1 U:UC 1=2:1.
б) Найдите площадь сечения параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью APQ.
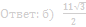
32. В правильной треугольной призме ABCA 1 B 1 C 1 сторона AB основания равна 12, а высота призмы равна 2. На рёбрах B 1 C 1 и AB отмечены точки P и Q соответственно, причём PC 1=3, а AQ = 4. ПлоскостьA 1 PQ пересекает ребро BC в точке M.
а) Докажите, что точка M является серединой ребра BC.
б) Найдите расстояние от точки B до плоскости A 1 PQ.
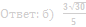
33. В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 2√3, а высота SHпирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамидыNSCD с вершиной N и основанием SCD.
а) Докажите, что точка T является серединой SM.
б) Найдите расстояние между NT и SC.
Ответ: б) √15/5
34. Дан прямой круговой конус с вершиной M. Осевое сечение конуса — треугольник с углом 120◦ при вершине M. Образующая конуса равна 2√3. Через точку M проведено сечение конуса, перпендикулярное одной из образующих.
а) Докажите, что получившийся в сечении треугольник тупоугольный.
б) Найдите площадь сечения.
Ответ: б) 4√2
35. Основанием прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 является квадрат ABCD со стороной 5√2, высота призмы равна 2√14. Точка K — середина ребра BB 1 . Через точки K и C 1 проведенаплоскость α, параллельная прямой BD 1 .
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
Ответ: б) 26
36. Дана правильная пирамида SABCD. Точка M находится на SD так, что MS:SD=2:3. Точка P серединаAD. Точка Q середина BC.
а) Доказать, что сечение пирамиды плоскостью MQP – равнобедренная трапеция.
б) Найдите соотношение объемов.
Ответ: б) 2/7
37. Основание прямой треугольной призмы ABCA 1 B 1 C 1 является прямоугольный треугольник ABC с прямым углом C. Диагонали граней AA 1 B 1 B и BB 1 C 1 C равны 15 и 9 соответственно, AB=13.
а) Докажите, что треугольник A 1 C 1 B – прямоугольный.
б) Найти объем пирамиды AA 1 C 1 B.
Ответ: б) 20√14
38. Основанием прямой треугольной призмы ABCA 1 B 1 C 1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC 1 A 1 является квадратом.
а) Докажите, что прямые CA 1 и AB 1 перпендикулярны.
б) Найдите расстояние между прямыми CA 1 и AB 1, если AC = 4, BC = 7.
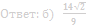
39. В правильной треугольной призме ABCA 1 B 1 C 1 сторона основания АВ равна 6, а боковое ребро AA 1равно 3. На ребре B 1 C 1 отмечена точка L так, что B 1 L=1. Точки К и М – середины ребер АВ и A 1 C 1соответственно. Плоскость ƴ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости ƴ
б) Найдите объем пирамиды, вершина которой – точка М, а основание – сечение данной призмы плоскостью ƴ.
Ответ: б) 5√3
40. В правильной четырехугольной призме KLMNK 1 L 1 M 1 N 1 точка E делит боковое ребро KK 1 в отношении KE:EK 1=1:3. Через точки L и E проведена плоскость α параллельная прямой KM и пересекающая ребро NN 1 в точке F.
а) Докажите, что плоскость α делит ребро NN 1 пополам.
б) Найдите угол между плоскостью α и плоскостью грани KLMN, если известно, что KL = 6, KK 1=4.
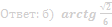
41. Основанием прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 является ромб ABCD, AB = AA 1 .
а) Докажите, что прямые A 1 C и BD перпендикулярны.
б) Найдите объем призмы, если A 1 C=BD=2.
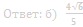
42. Ребро куба ABCDA 1 B 1 C 1 D 1 равно 6. Точки K, L и M — центры граней ABCD, AA 1 D 1 D и CC 1 D 1 Dсоответственно.
а) Докажите, что B 1 KLM — правильная пирамида.
б) Найдите объём B 1 KLM.
Ответ: б) 18
43. Длина диагонали куба ABCDA 1 B 1 C 1 D 1 равна 3. На луче A 1 C отмечена точка P так, что A 1 P=4.
а) Докажите, что PBDC 1 — правильный тетраэдр.
б) Найдите длину отрезка AP.
Ответ: б) √11
44. В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB=BC=AC=5√2.
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA=DN:NC=2:3. Найдите площадь сечения MNB.
Ответ: б) 3√6
45. В основании правильной треугольной пирамиды ABCD лежит треугольник ABC со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре AD отмечена точка T так, что AT:TD=2:1. Через точкуТ параллельно прямым AC и BD проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
Ответ: б) 20/3
46. Дан цилиндр, в котором проведены диаметры оснований. AB – диаметр верхнего основания, CD - диаметр нижнего, причем отрезки AB и CD не лежат на параллельных прямых.
а) Докажите, что у пирамиды ABCD противоположные ребра равны.
б) Найдите высоту цилиндра, если AC=7, AD=6, а радиус основания цилиндра равен 2,5.
Ответ: б) √30
47. SABCD — правильная пирамида с вершиной S. Из точки В опущен перпендикуляр BH на плоскостьSAD.
а) Доказать, что угол AHC=90°.
б) Найдите объем пирамиды, если HA=1 и HC=7.
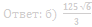
48. В кубе ABCDA 1 B 1 C 1 D 1 все рёбра равны 3. На его ребре BB 1 отмечена точка K так, что KB=2. Через точки K и C 1 проведена плоскость α, параллельная прямой BD 1 .
а) Докажите, что плоскость α проходит через середину ребра A 1 B 1 .
б) Найдите угол наклона плоскости α к плоскости грани BB 1 C 1 C.
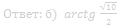
49. В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
Ответ: б) 64+32√3
50. В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 6.
а) Докажите, что угол между прямыми АС и BD 1 равен 60°.
б) Найдите расстояние между прямыми АС и BD 1 .
Ответ: б) 2√3
51. В правильной треугольной призме ABCA 1 B 1 C 1 все рёбра равны 2. Точка M — середина ребра AA 1 .
а) Докажите, что прямые MB и B 1 C перпендикулярны.
б) Найдите расстояние между прямыми MB и B 1 C.
Ответ: б) √30/5
52. В правильной четырёхугольной пирамиде PABCD сторона основания ABCD равна 12, боковое реброPA ―12√2. Через вершину A проведена плоскость a, перпендикулярная прямой PC и пересекающая ребро PC в точке K.
а) Докажите, что плоскость a делит высоту PH пирамиды PABCD в отношении 2:1, считая от вершины P.
б) Найдите расстояние между прямыми PH и BK.
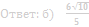
53. Дана правильная четырехугольная призма ABCDA 1 B 1 C 1 D 1. На ребре AA 1 отмечена точка K так, чтоAK: KA 1 = 1 : 2. Плоскость a проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD 1 в точке M.
а) Докажите, что MD:MD 1=2:1.
б) Найдите площадь сечения, если AB=4, AA 1=6.
Ответ: б) 8√6
54. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q,причём AQ:OB=1:2. Точка P — середина ребра AS.
а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
Ответ: б) √5
55. В правильном тетраэдре АВС точка Н — центр грани АВС, а точка М — середина ребра СD.
а) Докажите, что прямые АВ и СD перпендикулярны.
б) Найдите угол между прямыми DН и ВМ.
56. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C 1 , причёмCC 1 — образующая цилиндра, а AC — диаметр основания. Известно, что ∠ ACB=30°, AB=√2, CC 1=2.
а) Докажите, что угол между прямыми AC 1 и BC равен 45°.
б) Найдите объём цилиндра.
Ответ: б) 4π
57. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки B 1 и C 1 , причемBB 1 — образующая цилиндра, а отрезок AC 1 пересекает ось цилиндра.
а) Докажите, что угол ABC 1 прямой.
б) Найдите угол между прямыми BB 1 и AC 1, если АВ = 6, BB 1=15, B 1 C 1=8.
58. В основании прямой треугольной призмы ABCA 1 B 1 C 1. лежит равнобедренный (AB = BC) треугольник ABC. Точки K и M — середины рёбер A 1 B 1 и AC соответственно.
а) Докажите, что KM = KB.
б) Найдите угол между прямой KM и плоскостью ABB 1 , если AB = 8, AC = 6 и AA 1 = 3.
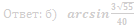
59. Дана правильная треугольная призма ABCA 1 B 1 C 1, у которой сторон основания равна 2, а боковое ребро равно 3. Через точки A, C 1 и середину T ребра A 1 B 1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Ответ: б) arctg 3
60. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 стороны основания равны 4, а боковые ребра 5.
а) Докажите, что плоскость A 1 C 1 E перпендикулярна плоскости BB 1 E 1 .
б) Найдите угол между плоскостями A 1 C 1 E и ABC.
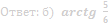
61. В треугольной пирамиде SABC основанием является правильный треугольник ABC, а ребро SBперпендикулярно плоскости основания. Точки D, E и F середины ребер AB, BC и BS соответственно.
а) Докажите, что плоскость DEF делит пополам высоту пирамиды, проведенную из вершины B.
б) Найдите расстояние от точки B до плоскости DEF, если AB=6, AS=10.
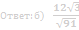
62. В основании пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=√33, все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребре AS – точка F так, что SF=BE=3.
а) Докажите, что плоскость CEF параллельна SB.
б) Пусть плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от Q до плоскости АВС.
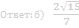
63. Дана правильная четырехугольная пирамида MABCD, все ребра которой равны 12. Точка N – середина бокового ребра MA, точка K делит боковое ребро MB в отношении 2:1, считая от вершины M.
а) Докажите, что сечение пирамиды плоскостью, проходящей через точки N и K параллельно прямой AD, является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Ответ: б) 7√51
64. На окружности основания конуса с вершиной S отмечены точки A, B и C так, что AB=BC.МедианаAM треугольника ASC пересекает высоту конуса.
а) Точка N - середина отрезка AC. Докажите, что MNB прямой.
б) Найдите угол между прямыми AM и SB, если AS=2, AC=√6.
65. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 6. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды.
Ответ: б) 12√3
66. В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 5, а сторона основания равна 4. На продолжении ребра SA за точку A отмечена точка P, а на продолжении ребра SB за точку B —точка Q, причём AP = BQ = SA.
а) Докажите, что прямые PQ и SC перпендикулярны друг другу.
б) Найдите угол между плоскостями ABC и CPQ.
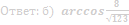
67. Плоскость α проходит через середину ребра AD прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1. перпендикулярно прямой BD 1 .
а) Докажите, что угол между плоскостью α и плоскостью ABC равен углу между прямыми BB 1 и B 1 D.
б) Найдите угол между плоскостью α и плоскостью ABC, если объём параллелепипеда ABCDA 1 B 1 C 1 D 1равен 48√3, AB = 2√3 и AD = 6.
Ответ: б) 60°
68. На ребре AA 1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 взята точка Е так, что A 1 E=6AE.Точка Т - середина ребра B 1 C 1 . Известно, что АВ =4√2, AD=12, AA 1=14.
a) Докажите, что плоскость ETD 1 делит ребро BB 1 в отношении 4:3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD 1 .
Ответ: б) 90
Задание № 15. Неравенство.
1. Решите неравенство:
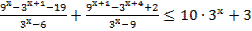
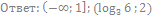
2. Решите неравенство:
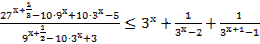
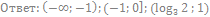
3. Решите неравенство:
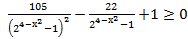
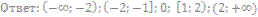
4. Решите неравенство:
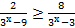
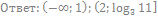
5. Решите неравенство:
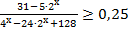
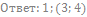
6. Решите неравенство:
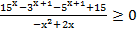
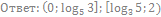
7. Решите неравенство:
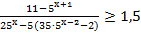
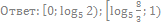
8. Решите неравенство:
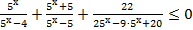
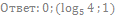
9. Решите неравенство:
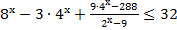
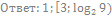
10. Решите неравенство:
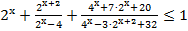
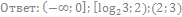
11. Решите неравенство:
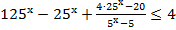
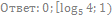
12. Решите неравенство:
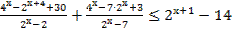
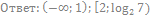
13. Решите неравенство:
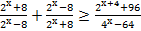
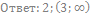
14. Решите неравенство:
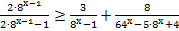
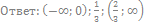
15. Решите неравенство:
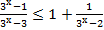
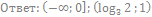
16. Решите неравенство:
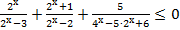
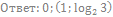
17. Решите неравенство:
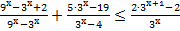
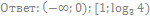
18. Решите неравенство:
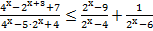
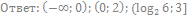
19. Решите неравенство:
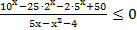
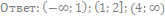
20. Решите неравенство:
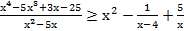
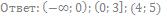
21. Решите неравенство:
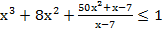
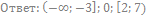
22. Решите неравенство:
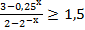
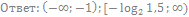
23. Решите неравенство:
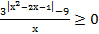
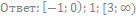
24. Решите неравенство:
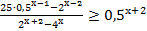
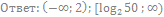
25. Решите неравенство:
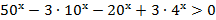
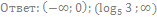
26. Решите неравенство:
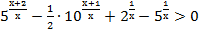
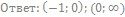
27. Решите неравенство:
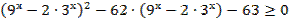
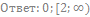
28. Решите неравенство:
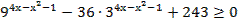
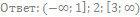
29. Решите неравенство
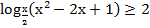
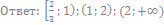
30. Решите неравенство:
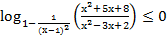

31. Решите неравенство:

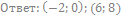
32. Решите неравенство:
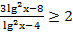
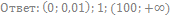
33. Решите неравенство:
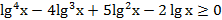
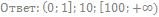
34. Решите неравенство:
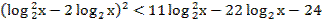

35. Решите неравенство:
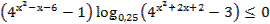
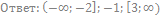
36. Решите неравенство:
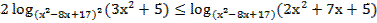
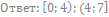
37. Решите неравенство:
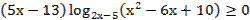
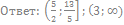
38. Решите неравенство:
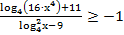
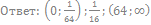
39. Решите неравенство:
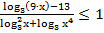
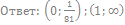
40. Решите неравенство:
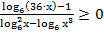
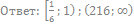
41. Решите неравенство:
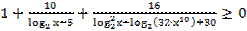
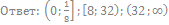
42. Решите неравенство:
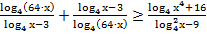
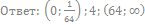
43. Решите неравенство:
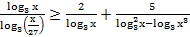
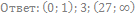
44. Решите неравенство:
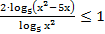
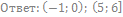
45. Решите неравенство:
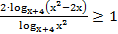
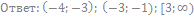
46. Решите неравенство:
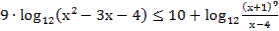

47. Решите неравенство:
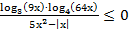
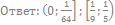
48. Решите неравенство:
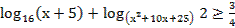
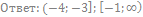
49. Решите неравенство:
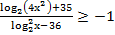
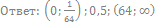
50. Решите неравенство:
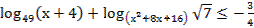
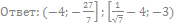
51. Решите неравенство:
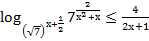
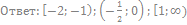
52. Решите неравенство:
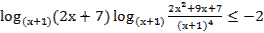
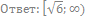
53. Решите неравенство:
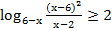
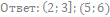
54. Решите неравенство:
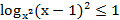
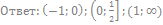
55. Решите неравенство:
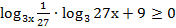
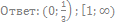
56. Решите неравенство:
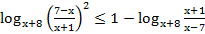
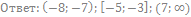
57. Решите неравенство:
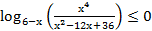
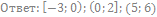
58. Решите неравенство:
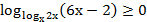
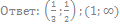
59. Решите неравенство:
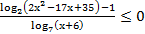
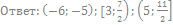
60. Решите неравенство:
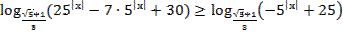
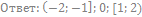
61. Решите неравенство:
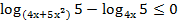
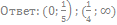
62. Решите неравенство:
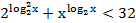
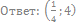
63. Решите неравенство:

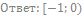
64. Решите неравенство:
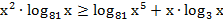
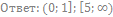
65. Решите неравенство:
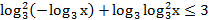
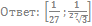
66. Решите неравенство:
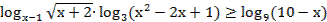
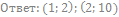
67. Решите неравенство:
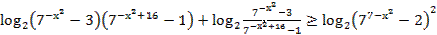
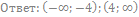
68. Решите неравенство:
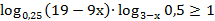
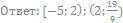
69. Решите неравенство:
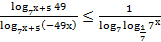
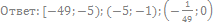
70. Решите неравенство:
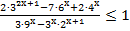
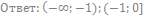
71. Решите неравенство:
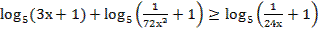
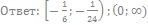
72. Решите неравенство:

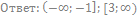
73. Решите неравенство:
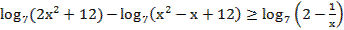

74. Решите неравенство:
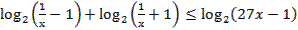
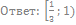
75. Решите неравенство:
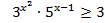
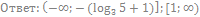
76. Решите неравенство:
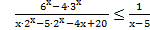
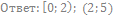
77. Решите неравенство:
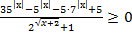
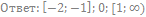
78. Решите неравенство:
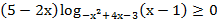
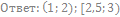
Задание № 17. Финансовая математика.
1. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S - целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.
Ответ: 36 млн
2. 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r - целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
Ответ: 7%
3. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S - целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором общая сумма выплат будет больше 10 млн рублей.
Ответ: 7 млн
4. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S - натуральное число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором общая сумма выплат будет составлять целое число миллионов рублей.
Ответ: 8 млн
5. В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S - натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Ответ: 200 тыс.
6. В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S - целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наибольшее значение S, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
Ответ: 13 млн
7. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Ответ: 22,5%
8. 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
Ответ: 3%
9. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
—с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший — не менее 0,6 млн рублей.
Ответ: 20%
10. В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Ответ: 80,5 млн
11. Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 7 млн рублей.
Ответ: 3 млн
12. В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия:
− каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017,2018 и 2019 долг остаётся равным S тыс. рублей;
− выплаты в 2020 и 2021 годах равны по 360 тыс. рублей;
− к июлю 2021 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Ответ: 1050 т
13. В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
Ответ: 10
14. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного его погашения равнялась 1 млн рублей?
Ответ: 0,8 млн
15. В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн рублей?
Ответ: 20,25 млн
16. В июле планируется взять кредит в банке на сумму 7 млн рублей на срок 10 лет. Условия возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь необходимо выплатить часть долга так, чтобы на начало июля каждого года долг уменьшался на одну и ту же сумму по сравнению с предыдущим июлем.
Найдите наименьшую возможную ставку r, если известно, что последний платёж будет не менее 0,819 млн рублей.
Ответ: 17%
17. В августе 2020 года взяли кредит. Условия возврата таковы:
— каждый год долг увеличивается на r%;
— с февраля по июль необходимо выплатить часть долга.
Кредит можно выплатить за четыре года равными платежами по 777 600 рублей, или за два года равными платежами по 1 317 600 рублей. Найдите r.
Ответ: 20%
18. 15-го января планируется взять кредит в банке на некоторое количество месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит.
Ответ: 19
19. Взяли кредит в банке на сумму 250 000 рублей под r% процентов годовых и выплатили за 2 года платежами 150 000 рублей в первый год и 180 000 рублей — во второй. Найдите r.
Ответ: 20%
20. Взяли кредит 177 120 рублей в банке на четыре года под 25% годовых и выплатили четырьмя равными платежами. Чему будет равна общая сумма выплат после полного погашения кредита?
Ответ: 300000 р
21. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга.
Определите, на какую сумму взяли кредита банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 78 030 рублей больше суммы взятого кредита.
Ответ: 119700 р
22. В июле 2020 года планируется взять кредит в банке на сумму 147 000 рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен двумя равными платежами, то есть за два года.
Ответ: 169400 р
23. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
− каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплачивать часть долга.
Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите r.
Ответ: 10%
24. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 1 млн рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 10 млн рублей.
Ответ: 6 млн
25. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвертого годов вкладчик ежегодно пополняет вклад на х млн рублей, где х – целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 7 млн рублей.
Ответ: 8 млн
26. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором банк за четыре года начислит на вклад больше 5 млн рублей.
Ответ: 9 млн
27. В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?
Ответ: 3110400 р
28. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,16 млн рублей.
Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами (то есть за 3 года)?
Ответ: 4,55 млн
29. В июле планируется взять кредит на сумму 4026000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом прошлого года.
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей больше придется отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года) по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
Ответ: 950400 р
30. В июле планируется взять кредит в банке на сумму 100000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на а% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга.
Найдите число а, если известно, что кредит был полностью погашен за два года, причем в первый год было переведено 55000 руб., а во второй 69000 рублей.
Ответ: 15%
31. В июле планируется взять кредит в банке на сумму 6 млн рублей на некоторый срок.Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил 1,8 млн рублей?
Ответ: 10 лет
32. В июле планируется взять кредит в банке на сумму 10 млн рублей на 5 лет. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Сколько млн рублей составила общая сумма выплат после погашения кредита?
Ответ: 13 млн
33. В июле планируется взять кредит в банке на сумму 1300000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
На какое минимально количество лет можно взять кредит при условии, что ежегодные выплаты были не более 350000 рублей?
Ответ: 5 лет
34. Бизнес-проект «А» предполагает в течение первых двух лет рост вложенных в него сумм на 34,56% ежегодно и на 44% ежегодно в течение следующих двух лет. Проект «Б» предполагает рост на постоянное целое число n процентов ежегодно. Найдите наименьшее значение n, при котором за первые четыре года проект «Б» будет выгоднее проекта «А».
Ответ: 39,2%
35. Вася взял кредит в банке на сумму 270 200 рублей. Схема выплата кредита такова: в конце каждого года банк увеличивает на 10 % оставшуюся сумму долга, а затем Вася переводит в банк свой очередной платеж. Известно, что Вася погасил кредит за три года, причем каждый его следующий платеж был ровно втрое больше предыдущего. Какую сумму Вася заплатил в первый раз? Ответ дайте в рублях.
Ответ: 26620 рублей
36. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 680
37. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4 t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 410 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
Ответ: 2050000 р
38. Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей. Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 100
39. Строительство нового завода стоит 75 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5х2+x+7 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px-(0,5x2+x+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?
Ответ: 9000 р
40. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t ( t=1; 2; …). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 10%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей?
Ответ: 21 год
41. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1+r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?
Ответ: 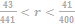
42. Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объёме t2 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме t2 Гбайт входящей в него информации выходит 21t Гбайт обработанной информации; 25 < t < 55. Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 Гбайт?
Ответ: 1682
43. Зависимость объема Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой Q=15000-P, 1000≤P≤15000. Доход от продажи товара составляет PQ рублей. Затраты на производство Q единиц товара составляют 3000Q+5000000 рублей.Прибыль равна разности дохода от продажи товара и затрат на его производство.Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Ответ: 12,5%
44. Зависимость количества Q (в шт. 0≤Q≤15000) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q=15000-P. Затраты на производство Q единиц товара составляют3000Q+10000000 рублей. Кроме затрат на производство, фирма должна платить налог t рублей (0 < t < 10000) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет PQ-3000Q-10000000-tQ рублей, а общая сумма налогов, собранных государством, равна tQ рублей. Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
Ответ: 6000
45. В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется t2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?
Ответ: 120 кг
46. У фермера есть два поля, каждое площадью 15 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 400 ц/га.
Фермер может продавать картофель по цене 2000 руб. за центнер, а свёклу — по цене 3000 руб. за центнер. Какой наибольший доход может получить фермер?
Ответ: 30 млн рублей
47. Производство x тыс. единиц продукции обходится в q = 0,5x2 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
Ответ: 9
48. В регионе А среднемесячный доход на душу населения в 2014 году составлял 43740 рублей и ежегодно увеличивался на 25%. В регионе Б среднемесячный доход на душу населения в 2014 году составлял 60000 рублей. В течение трех лет суммарный доход жителей региона Б увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах А и Б стал одинаковым. Найдите m.
Ответ: 4
49. По бизнес-плану четырёхлетний проект предполагает начальное вложение 12 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в конце первого и второго года, а также целое число m млн рублей в конце третьего и четвёртого года. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Ответ: 4 и 2 млн руб.
50. По вкладу «А» банк в конце каждого года планирует увеличивать на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 8 % в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Ответ: 12
Задание № 16. Планиметрия с доказательством.
1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ ABM= ∠ DBС=30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC=9.
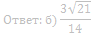
2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3
3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P,причём BC=CD.
а) Докажите, что AB:BC=AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности,AB=6, а BC=6√2.
Ответ: б) 18√3
4. В треугольнике ABC точки A 1 , B 1 , C 1 — середины сторон BC, AC и AB соответственно, AH— высота,∠ BAC=60°, ∠ BCA=45°.
а) Докажите, что точки A 1 , B 1 , C 1, H— лежат на одной окружности.
б) Найдите A 1 H, если BC=2√3.
Ответ: б) 1
5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC=16.
Ответ: б) √10
6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точкеM, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Qсоответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠ AOC=√15/4.Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4
7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM=LB:LA.
б) Найдите MN, если LB:LA=2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6
8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN=4 и AM:MC=1:3.
Ответ: б) 7
9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметромBC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MBпересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK=3 и MK=12.
Ответ: б) 30
10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MDперпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM,BN и CN, равна 18.
Ответ: б) 96
11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HMсоответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB=5, AC=8.
Ответ: б) 2,88
12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC=∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC=55°.
Ответ: б) 175
13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношенииAP:PB=CQ:QB=CW:WD=3:4, радиус окружности, описанной около треугольника PQW, равен 10,PQ=16, QW=12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
Ответ: б) 392
14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C 1 , B 1соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB 1 C 1 .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А= 45°, B 1 C 1= 6 и площадь треугольника AB 1 C 1 в восемь раз меньше площади четырёхугольника BCB 1 C 1.

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC=15 и BD=8,5.
Ответ: б) 8
16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВСсоответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН=12 и ВН=3.
Ответ: б) 50
17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороныAC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65
18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикулярыМЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4
19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и Cсоответственно.
а) Докажите, что 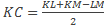 .
.
б) Найдите отношение LB:BM, если известно, что KC:CM=3:2 и ∠ MKL=60.
Ответ: б) 5:2
20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3
21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE=AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD=15.
Ответ: б) 2:1
22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BCсоответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC=7/25.
Ответ: б) 25:36
23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB иBC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4
24. На катетах AC и BC прямоугольного треугольника ABC как диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC.Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM=1, BM=3, а Q – середина дуги MB.
Ответ: б) 2
25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.
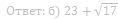
26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, чтоAP/PD=sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.
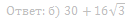
27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD=sin∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD=90, а основания равны 5 и 7.
Ответ: б) 35
28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
Ответ: б) 60
29. Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.
а) Доказать, что M делит AD в отношении 2:1.
б) Найдите расстояние от точки C до середины BD, если AD = 18, AC =4√13.
Ответ: б) 4
30. В трапеции АBCD ∠BAD прямой. Окружность, построенная на большем основании АD как на диаметре, пересекает меньшее основание BC в точке C и M.
а) Докажите, что ∠BАM равен ∠CАD.
б) Диагонали трапеции АBCD пересекаются в точке O. Найдите площадь треугольника АOB, если АB = 6, а BC = 4BM.
Ответ: б) 20
31. Известно, что АBCD трапеция, АD = 2BC, AD, BC — основания. Точка M такова, что ∠ АBM и ∠MCDпрямые.
а) Доказать, что MA = MD.
б) Расстояние от M до AD= BC, а ∠ АDC равен 55. Найдите ∠ BAD.
Ответ: б) 80
32. Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/64 от площади трапеции ABCD.
Ответ: б) 3:5
33. Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и Nсоответственно. Известно, что AM = 8MB и DN = 2CN.
а) Докажите, что AD = 4BC.
б) Найдите длину отрезка MN, если радиус окружности равен √6.
Ответ: б) 4
34. В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.
а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD=4.
Ответ: б) 2/9
35. Две окружности с центрами O 1 и O 2 и радиусами 3 и 4 пересекаются в точках A и B. Через точку Aпроведена прямая MK пересекающая обе окружности в точках M и K, причем точка A находится между ними.
а) Докажите, что треугольники BMK и O 1 AO 2 подобны.
б) Найдите расстояние от точки B до прямой MK, если O 1 O 2 = 5, MK = 7.
Ответ: б) 84/25
36. Две окружности с центрами O 1 и O 2 пересекаются в точках A и B, причём точки O 1 и O 2 лежат по разные стороны от прямой AB. Продолжения диаметра CA первой окружности и хорды CB этой окружности пересекают вторую окружности в точках D и E соответственно.
а) Докажите, что треугольники CBD и O 1 AO 2 подобны.
б) Найдите AD, если ∠ DAE = ∠BAC радиус второй окружности в четыре раза больше радиуса первой иAB=2.
Ответ: б) 8
37. В прямоугольном треугольнике ABC проведена высота CH из вершины прямого угла. В треугольникиACH и BCH вписаны окружности с центрами O 1 и O 2 соответственно, касающиеся прямой CH в точкахM и N соответственно.
а) Докажите, что прямые AO 1 и CO 2 перпендикулярны.
б) Найдите площадь четырёхугольника MO 1 NO 2, если AC = 20 и BC = 15.
Ответ: б) 3,5
38. Дана трапеция ABCD с боковой стороной AB, которая перпендикулярна основаниям. Из точки А на сторону CD опущен перпендикуляр AH. На стороне AB взята точка E так, что прямые СЕ и СDперпендикулярны.
а) Доказать, что прямые BH и ED параллельны.
б) Найти отношение BH к ED, если ∠ BCD=135.
Ответ: б) 1:2
39. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17.
а) Докажите, что данный четырехугольник ‐ трапеция.
б) Найдите отношение оснований этой трапеции.
Ответ: б) 2:5
40. Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BE пересекается с прямой CK в точке O.
а) Докажите, что вокруг четырёхугольника ABOK можно описать окружность.
б) Найдите AO, если сторона квадрата равна 1.
Ответ: б) 1
41. На продолжении стороны АС за вершину А треугольника АВС отмечена точка D так, что AD = AB. Прямая, проходящая через точку А, параллельно BD, пересекает сторону ВС в точке M.
а) Докажите, что AM — биссектриса треугольника АВС.
б) Найти площадь SAMBD, если AC = 30, BC = 18 и AB = 24.
Ответ: б) 268,8
42. В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину Вперпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) Докажите, что биссектриса угла С делит отрезок МN пополам
б) Пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Ответ: б) 3:1
43. Диагональ AC разбивает трапецию ABCD с основанием AD и BC, из которых AD большее, на два подобных треугольника.
а) Докажите, что ∠ABC = ∠ACD.
б) Найдите отрезок, соединяющий середины оснований трапеции, если известно, что BC = 18, AD = 50 иcos ∠ CAD=3/5.
Ответ: б) 8√13
44. К двум непересекающимся окружностям равных радиусов проведены две параллельные общие касательные. Окружности касаются одной из этих прямых в точках A и B. Через точку C, лежащую на отрезке AB, проведены касательные к этим окружностям, пересекающие вторую прямую в точках D и E,причём отрезки CA и CD касаются одной окружности, а отрезки CB и CE — другой.
а) Докажите, что периметр треугольника CDE вдвое больше расстояния между центрами окружностей.
б) Найдите DE, если радиусы окружностей =5, расстояние между их центрами =18, а AC = 8.
Ответ: б) 12,375
45. Высоты BB 1 и CC 1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠AHB 1 = ∠ACB.
б) Найдите BC, если AH = 21 и ∠BAC = 30°.
Ответ: б) 7√3
46. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на стороне BC, а вершина E— на стороне AB.
а) Докажите, что FH = 2DH.
б) Найдите площадь прямоугольника DEFH, если AB = 2.
Ответ: б) 6-3√3
47. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AKпересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Ответ: б) 3,2
48. Точки A 1 , B 1 , C 1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что отличная от A 1 точка пересечения окружностей, описанных около треугольниковA 1 CB 1и A 1 BC 1, лежит на окружности, описанной около треугольника B 1 AC 1.
б) Известно, что AB = AC = 10 и BC = 12. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры окружностей, описанных около треугольников A 1 CB 1, A 1 BC 1 иB 1 AC 1.
Ответ: б) 1,5
49. В треугольник ABC, в котором длина стороны AC меньше длины стороны BC, вписана окружность с центром O. Точка B 1 AC 1 симметрична точке B относительно CO.
а) Докажите, что A, B, O и B 1 лежат на одной окружности.
б) Найдите площадь четырёхугольника AOBB 1, если AB = 10, AC = 6 и BC = 8.
Ответ: б) 18
50. Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M, а окружность с диаметром CD пересекает основание AD в точке N. Отрезки AM и CN пересекаются в точке P.
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC=7, AD=17.
Ответ: б) 4,2
51. Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK:KC=1:2.
а) Докажите, что ∠BAC=30°.
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK — в точке Q. Найдите KQ, еслиBC=√21.
Ответ: б) 14
52. В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и ADсоответственно. Площади четырёхугольников ABLN и NLCD равны, а площади четырёхугольниковKBCM и AKMD относятся как 11:17.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите отношение BC к AD.
Ответ: б) 0,4
53. Точка О — центр окружности, описанной около остроугольного треугольника ABC. На продолжении отрезка AO за точку О отмечена точка K так, что ∠BAC+∠AKC=90°.
а) Докажите, что четырехугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около треугольника KBC, если известно, что радиус окружности, описанной около треугольника АBC равен 12, а cos∠BAC=0,6.
Ответ: б) 10
54. В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.
Ответ: б) 1:15
55. Около равнобедренного треугольника ABC с основанием BC описана окружность. Через точку C провели прямую, параллельную стороне AB. Касательная к окружности, проведённая в точке B, пересекает эту прямую в точке K.
а) Докажите, что треугольник BCK — равнобедренный.
б) Найдите отношение площади треугольника ABC к площади треугольника BCK, если cos∠BAC=3/4.
Ответ: б) 2
56. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.
а) Докажите, что BM и ВD делят угол В на три равных угла.
б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCD до прямой СМ, если BC=6√21.
Ответ: б) 3
57. Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований.
а) Докажите, что расстояние между центрами окружностей равно большей боковой стороне трапеции.
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные 2 и 50.
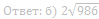
58. В остроугольном треугольнике ABC проведены высоты AK и CM. На них из точек M и K опущены перпендикуляры ME и KH соответственно.
а) Докажите, что прямые EH и AC параллельны.
б) Найдите отношение EH и AC, если ∠ ABC=45°
Ответ: б) 1:2
59. Точка М – середина гипотенузы АВ треугольника АВС. Серединный перпендикуляр к гипотенузе пересекает катет ВС в точке N.
а) Докажите, что ∠ CAN = ∠ CMN
б) Найдите отношение радиусов окружностей, описанных около треугольников ANB и CBM, если tg BAC = 4/3.
Ответ: б) 5:4
60. В равнобедренной трапеции ABCD основание AD в два раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.
б) Пусть O — точка пересечения диагоналей трапеции ABCD. Найдите расстояние от вершины C до середины отрезка OD, если BC=16 и AB=10.
Ответ: б) 4
61. В трапеции ABCD основание AD в два раза больше основания BC. Внутри трапеции взяли точку Mтак, что углы ABM и DCM прямые.
а) Докажите, что AM=DM.
б) Найдите угол BAD, если угол ADC равен 70°, а расстояние от точки M до прямой AD равно сторонеBC.
Ответ: б) 65°
62. Около остроугольного треугольника ABC описана окружность с центром O. На продолжении отрезкаAO за точку O отмечена точка K так, что ∠ BAC +∠AKC=90°.
а) Докажите, что четырёхугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если cos ∠BAC=3/5, а BC=48.
Ответ: б)25
63. В равнобедренной трапеции ABCD основание AD в три раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых вдвое больше другого.
б) Найдите расстояние от вершины C до середины диагонали BD, если AD=15 и AC=2√61.
Ответ: б) 6
64. В трапеции ABCD боковая сторона AB перпендикулярна основаниям.
Из точки A на сторону CD опустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямыеCD и CE перпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH к ED, если ∠ BCD=120°.
Ответ: б) 3:4
65. В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHC равен 60°.
а) Докажите, что угол ABC равен 120°.
б) Найдите BH, если AB=4, AA 1=6.
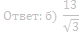
66. В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые.
а) Докажите, что АВ = CD.
б) Найдите AD, если AB = 2, BC = 7.
Ответ: б) 8
67. Точка Е — середина стороны BС квадрата АВСD. Серединные перпендикуляры к отрезкам АЕ и ЕС пересекаются в точке O.
а) Докажите, что ∠ AOE=90°.
б) Найдите BO:OD.
Ответ: б) 3:1
68. Точка O — центр окружности, описанной около остроугольного треугольника ABC, а BH — высота этого треугольника.
а) Докажите, что углы ABH и CBO равны.
б) Найдите BH, если AB=8, BC=9, BH=BO.
Ответ: б) 6
69. В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
б) Найдите BD.
Ответ: б) 55/7
70. Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB=BC=CD=12.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите AD.
Ответ: б) 9
71. Окружность с центром О1 касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O2 касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.
а) Докажите, что прямая О1О2 параллельна основаниям трапеции АВСD.
б) Найдите О1О2.
Ответ: б) 4
72. Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4.
Ответ: б) 24
73. Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D.
а) Докажите, что AE = AK.
б) Найдите AD, если CE =10, DK = 9 и cos ∠ BAD=0,2.
Ответ: б) 40
74. Высоты тупоугольного треугольника АВС с тупым углом АВС пересекаются в точке Н. Угол АНСравен 60 градусов.
а) Докажите, что угол АВС равен 120 градусов
б) Найдите ВН, если АВ=7, ВС=8.
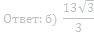
75. В трапецию ABCD c основаниями ВС и AD вписана окружность с центром О, СН – высота трапеции,Е – точка пересечения диагоналей.
а) Докажите, что 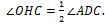
б) Найдите площадь четырехугольника СЕОН, если известно, что ∠BAD=90°, BC=9, AD=18.
Ответ: б) 21
76. Серединный перпендикуляр к стороне АВ треугольника АВС пересекает сторону АС в точке D.Окружность с центром О, вписанная в треугольник ADB, касается отрезка AD в точке Р, а прямая ОРпересекает сторону АВ в точке К.
а) Докажите, что около четырехугольника ВDОК можно описать окружность.
б) Найдите радиус этой окружности, если АВ = 10, АС = 8, ВС = 6.
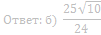
77. Окружность, вписанная в треугольник ABC, касается сторон BC и AC в точках M и N соответственно,E и F — середины сторон AB соответственно. Прямые MN и EF пересекаются в точке D.
а) Докажите, что треугольник DFN равнобедренный.
б) Найдите площадь треугольника BE, если AB = 20и ∠ ABC = 60°.
78. Медианы AA 1 , BB 1 , CC 1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA 1 и CC 1 , если известно, что AC = 12.
Ответ: б) 180
79. Четырёхугольник ABCD вписан в окружность. Диаметр CC 1 перпендикулярен стороне AD и пересекает её в точке M, а диаметр DD 1 перпендикулярен стороне AB и пересекает её в точке N.
а) Пусть AA 1 также диаметр окружности. Докажите, что ∠ DNM = ∠ BA 1 D 1 .
б) Найдите углы четырёхугольника ABCD, если угол CDB вдвое меньше угла ADB.
Ответ: б) 72°, 126°, 108°, 54°
80. В прямоугольном треугольнике ABC с прямым углом C известны стороны AC =12, BC = 5.Окружность радиусом 0,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.
а) Докажите, что радиус второй окружности меньше, чем 1/5 длины катета AC.
б) Найдите радиус второй окружности.
Ответ: б) 2
81. Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T.
а) Докажите, что угол BOC вдвое больше угла BTC.
б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно.
Ответ: б) 6
82. Окружность с центром O, вписанная в треугольник ABC, касается его сторон BC, AB и AC в точках K, L и M соответственно. Прямая KM вторично пересекает в точке P окружность радиуса AM с центром A.
а) Докажите, что прямая AP параллельна прямой BC.
б) Пусть ∠ ABC = 90°, AM = 3, CM = 2, Q — точка пересечения прямых KM и AB, а T —такая точка на отрезке PQ, что ∠ OAT = 45°. Найдите QT.
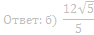
Задание № 18. Задачи с параметром.
1. Найдите значения a, при каждом из которых система уравнений
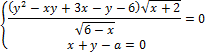
имеет ровно два решения.
2. Найдите значения a, при каждом из которых система уравнений
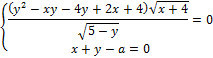
имеет единственное решение.
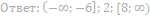
3. Найдите значения a, при каждом из которых система уравнений
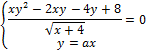
имеет ровно два решения.
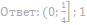
4. Найдите значения a, при каждом из которых система уравнений
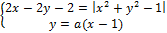
имеет более двух решений.
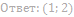
5. Найдите значения a, при каждом из которых система уравнений
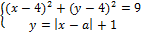
имеет ровно три решения.
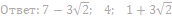
6. Найдите значения a, при каждом из которых система уравнений
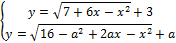
имеет единственное решение.
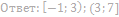
7. Найдите значения a, при каждом из которых система уравнений
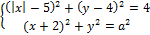
имеет единственное решение.
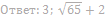
8. Найдите значения a, при каждом из которых система уравнений
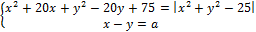
имеет более одного решения.
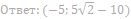
9. Найдите значения a, при каждом из которых система уравнений
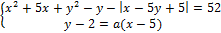
имеет ровно два решения.
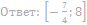
10. Найдите значения a, при каждом из которых система уравнений
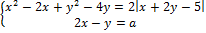
имеет более двух решений.
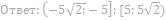
11. Найдите значения a, при каждом из которых система уравнений
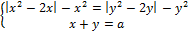
имеет более двух решений.
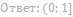
12. Найдите значения a, при каждом из которых система уравнений
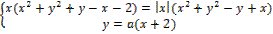
имеет ровно три различных решения.
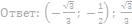
13. Найдите значения a, при каждом из которых система уравнений
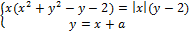
имеет ровно три различных решения.
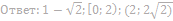
14. Найдите значения a, при каждом из которых система уравнений
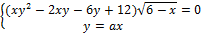
имеет ровно три решения.
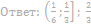
15. Найдите значения a, при каждом из которых система уравнений
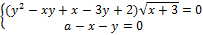
имеет ровно два решения.
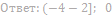
16. Найдите значения a, при каждом из которых система уравнений
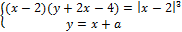
имеет ровно четыре решения.
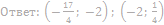
17. Найдите значения a, при каждом из которых система
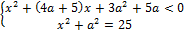
имеет решения.
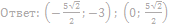
18. Найдите значения a, при каждом из которых система
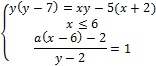
имеет единственное решение.
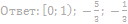
19. Найдите значения a, при каждом из которых система
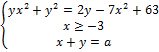
имеет ровно два различных решения.
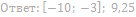
20. Найдите значения a, при каждом из которых система неравенств
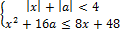
имеет хотя бы одно решение на отрезке [0;1].
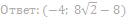
21. Найдите значения a, при каждом из которых система неравенств
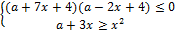
имеет хотя бы одно решение.
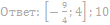
22. Найдите значения a, при каждом из которых система неравенств
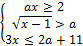
имеет хотя бы одно решение на отрезке [3; 4].
23. Найдите значения a, при каждом из которых наименьшее значение функции
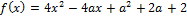
на множестве │x│≥1 не менее 6.
24. Найдите значения a, при каждом из которых уравнение
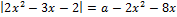
либо не имеет решений, либо имеет единственное решение
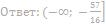
25. Найдите значения a, при каждом из которых уравнение
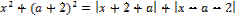
имеет единственное решение.
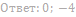
26. Найдите значения a, при каждом из которых уравнение
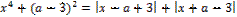
либо не имеет решений, либо имеет единственное решение.
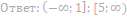
27. Найдите значения a, при каждом из которых уравнение
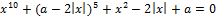
имеет более трех различных решений.
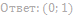
28. Найдите значения a, при каждом из которых уравнение
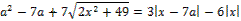
имеет хотя бы один корень.
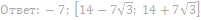
29. Найдите значения a, при каждом из которых уравнение
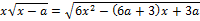
имеет ровно один корень на отрезке [0;1].
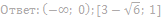
30. Найдите значения a, при каждом из которых уравнение
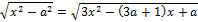
имеет ровно один корень на отрезке [0;1].
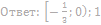
31. Найдите значения a, при каждом из которых уравнение
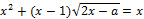
имеет ровно один корень на отрезке [0;1].
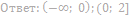
32. Найдите значения a, при каждом из которых уравнение
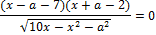
имеет ровно один корень на отрезке [4;8].
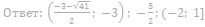
33. Найдите значения a, при каждом из которых уравнение
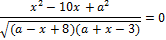
имеет ровно один корень на отрезке [2; 6].
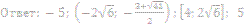
34. Найдите значения a, при каждом из которых уравнение
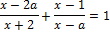
имеет ровно один корень.
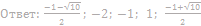
35. Найдите значения a, при каждом из которых уравнение
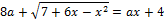
имеет единственный корень.
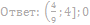
36. Найдите значения a, при каждом из которых уравнение
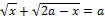
имеет ровно два различных корня.
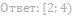
37. Найдите значения a, при каждом из которых уравнение
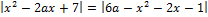
имеет более двух различных корней.
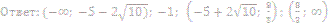
38. Найдите значения a, при каждом из которых уравнение
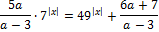
имеет ровно два различных корня.
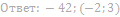
39. Найдите значения a, при каждом из которых уравнение
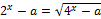
имеет единственный корень.
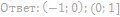
40. Найдите значения a, при каждом из которых уравнение
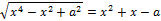
имеет ровно три различных корня.
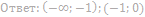
41. Найдите значения a, при каждом из которых уравнение
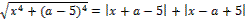
имеет единственное решение.
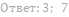
42. Найдите значения a, при каждом из которых уравнение
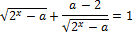
имеет ровно два различных корня.
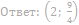
43. Найдите значения a, при каждом из которых уравнение
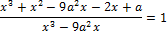
имеет ровно один корень.
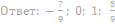
44. Найдите значения a, при каждом из которых уравнение
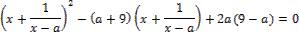
имеет ровно четыре решения.
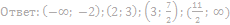
45. Найдите значения a, при каждом из которых уравнение

имеет ровно два решения.

46. Найдите значения a, при каждом из которых уравнение
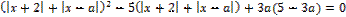
имеет ровно два решения.
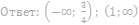
47. Найдите значения a, при каждом из которых уравнение
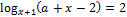
имеет хотя бы один корень, на промежутке (-1; 1]
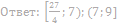
48. Найдите значения a, при каждом из которых уравнение
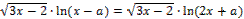
имеет ровно один корень, на промежутке [0;1]
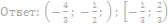
49. Найдите значения a, при каждом из которых уравнение
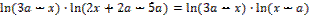
имеет ровно один корень, на промежутке [0;2]
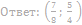
50. Найдите значения a, при каждом из которых уравнение
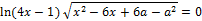
имеет ровно один корень, на промежутке [0;3]
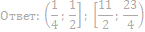
51. Найдите значения a, при каждом из которых решение уравнения
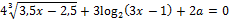
принадлежит отрезку [1;3].
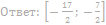
52. Найдите значения a, при каждом из которых уравнение
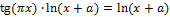
имеет ровно один корень, на промежутке [0;1)
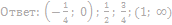
53. Найдите все значения a, при которых уравнение
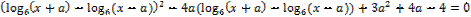
имеет ровно два решения.
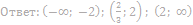
54. Найдите значения a, при каждом из которых уравнение
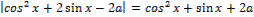
имеет на промежутке [-π/2; 0) единственный корень.
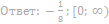
55. Найдите значения a, при каждом из которых уравнение
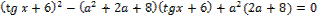
имеет на отрезке [0; 3π/2] ровно два решения.
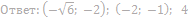
56. Найдите значения a, при каждом из которых уравнение
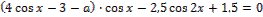
имеет хотя бы один корень.
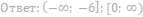
57. Найдите значения a, при каждом из которых уравнение
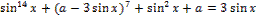
имеет хотя бы один корень.
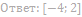
58. Найдите значения параметра a, при которых для любого действительного x выполняется неравенство
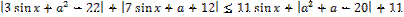
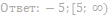
59. Найдите значения параметра a, при каждом из которых уравнение
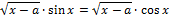
имеет ровно один корень на отрезке [0; π]
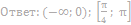
60. Найдите значения a, при каждом из которых неравенство
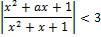
выполняется при всех x.
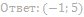
61. Найдите значения a, при каждом из которых множество решений неравенства
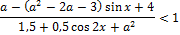
содержит отрезок [-2π; -7π/6]
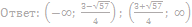
62. Найдите значения a, для каждого из которых существует хотя бы одна пара чисел x и y, удовлетворяющая неравенству
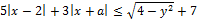
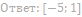
63. Найдите все значения параметра а, при каждом из которых система
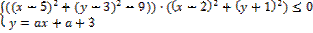
не имеет решений.
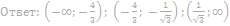
64. Найдите все значения параметра а, при каждом из которых система
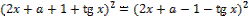
имеет на промежутке [-π/2; π/2] единственный корень.
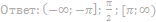
65. Найдите все значения a, при каждом из которых функция
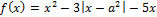
имеет более двух точек экстремума.
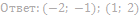
Задание № 19. Задачи на логику.
1. Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100.
а) Может ли частное этого числа и суммы его цифр быть равным 82?
б) Может ли частное этого числа и суммы его цифр быть равным 83?
в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Ответ: а) да; б) нет; в) 91
2. Задумано несколько целых чисел. Набор этих чисел и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Например, если задуманы числа 2, 3, 5, то на доске будет выписан набор 2, 3, 5, 5, 7, 8, 10.
а) На доске выписан набор − 8, − 5, − 4, − 3, − 1, 1, 4. Какие числа были задуманы?
б) Для некоторых различных задуманных чисел в наборе, выписанном на доске, число 0 встречается ровно 2 раза. Какое наименьшее количество чисел могло быть задумано?
в) Для некоторых задуманных чисел на доске выписан набор. Всегда ли по этому набору можно однозначно определить задуманные числа?
Ответ: а) -5, -3, 4; б) 4; в) нет
3. а) Существует ли конечная арифметическая прогрессия, состоящая из пяти натуральных чисел, такая, что сумма наибольшего и наименьшего членов этой прогрессии равна 99?
б) Конечная арифметическая прогрессия состоит из шести натуральных чисел. Сумма наибольшего и наименьшего членов этой прогрессии равна 9. Найдите все числа, из которых состоит эта прогрессия.
в) Среднее арифметическое членов конечной арифметической прогрессии, состоящей из натуральных чисел, равно 6,5. Какое наибольшее количество членов может быть в этой прогрессии?
Ответ: а) нет; б) 2, 3, 4, 5, 6, 7; в)12
4. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18, 20, 21, 23, 25, 27, 30, 32, 34, 41.
Ответ: а) 1, 1, 1, 1, 1, 1, 1; б) нет, в) 7, 7, 7, 9, 11 или 7, 9, 11, 14
5. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 2/11 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 2/5 от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 9 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов: а) и б)?
Ответ: а) да; б) 9; в) 9/17
6. В течение четверти учитель ставил школьникам отметки «1», «2», «3», «4» и «5». Среднее арифметическое отметок ученика оказалось равным 4,625.
а) Какое наименьшее количество отметок могло быть у ученика?
б) На какое наибольшее число может увеличиться среднее арифметическое отметок этого ученика после замены четырёх отметок «3», «3», «5» и «5» двумя отметками «4»?
Ответ: а) 8; б) на 5/24
7. Имеется 10 карточек. На них записывают по одному каждое из чисел 1, − 2,− 3, 4,− 5, 7,− 8, 9, 10,− 11. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному1, − 2,− 3, 4,− 5, 7,− 8, 9, 10,− 11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Ответ: а) нет; б) нет; в) 4
8. Моток верёвки режут без остатка на куски длиной не меньше 168 см, но не больше 175 см (назовём такие куски стандартными).
а) Некоторый моток верёвки разрезали на 24 стандартных куска, среди которых есть куски разной длины. На какое наибольшее число одинаковых стандартных кусков можно было бы разрезать тот же моток верёвки?
б) Найдите такое наименьшее число l, что любой моток верёвки, длина которого больше l см, можно разрезать на стандартные куски.
Ответ: а) 24; б) 4032
9. Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары групп находят модуль разности найденных сумм и полученные 6 чисел складывают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Каково наименьшее возможное значение полученного результата?
Ответ: а) нет; б) нет; в) 4
10. Имеется 25 коробок массой 31 кг каждая и 15 коробок массой 51 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S— модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S:
а) если дополнительно требуется, что в контейнерах должно находиться одинаковое количество коробок;
б) без дополнительного условия пункта а.
Ответ: а) 20; б) 2
11. По окружности расставляют 40 ненулевых целых чисел с общей суммой 16. При этом любые два стоящих рядом числа должны отличаться не более чем на 6 и среди любых четырёх подряд идущих чисел должно быть хотя бы одно положительное.
а) Среди таких 40 чисел найдите наибольшее возможное количество положительных.
б) Среди таких 40 чисел найдите наименьшее возможное количество положительных.
Ответ: а) 37; б) 10
12. Костя должен был умножить двухзначное число на трехзначное число (числа с нуля начинаться не могут). Вместо этого он просто приписал трехзначное число справа к двухзначному, получив пятизначное число, которое оказалось в N раз (N — натуральное число) больше правильного результата.
а) Могло ли N равняться 2?
б) Могло ли N равняться 10?
в) Каково наибольшее возможное значение N?
Ответ: а) да; б) нет; в) 9
13. Рассматриваются конечные непостоянные арифметические прогрессии, состоящие из натуральных чисел, которые не имеют простых делителей, отличных от 2 и 3.
а) Может ли в этой прогрессии быть три числа?
б) Какое наибольшее количество членов может быть в этой прогрессии?
Ответ: а) да; б) 4
14. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 2970. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 16 заменили на число 61).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 3 раза меньше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 5 раза меньше, чем сумма исходных чисел?
в) Найдите наименьшее возможное значение суммы получившихся чисел.
Ответ: а) пример: 32 раза число 92 и число 26; б) нет; в) 693
15. На доске было написано 20 натуральных чисел (необязательно различных), каждое из которых не превосходит 40. Вместо некоторых из чисел (возможно, одного) на доске написали числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, с доски стёрли.
а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось?
б) Среднее арифметическое первоначально написанных чисел равнялось 27. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 34?
в) Среднее арифметическое первоначально написанных чисел равнялось 27. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Ответ: а) да; б) нет; в) 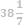
16. Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.
Ответ: а) да; б) нет; в) 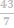
17. Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 10 раз больше, либо в 10 раз меньше предыдущего. Сумма всех членов последовательности равна 3024.
а) Может ли последовательность состоять из двух членов?
б) Может ли последовательность состоять из трёх членов?
в) Какое наибольшее количество членов может быть в последовательности?
Ответ: а) нет; б) да; в) 549
18. Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 720, и
а) пять;
б) четыре;
в) три
из них образуют геометрическую прогрессию?
Ответ: а) нет; б) нет; в) да
19. На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Ответ: а) 36; б) отрицательных; в) 16
20. Три числа назовём хорошей тройкой, если они могут быть длинами сторон треугольника. Три числа назовём отличной тройкой, если они могут быть длинами сторон прямоугольного треугольника.
а) Даны 8 различных натуральных чисел. Может ли оказаться, что среди них не найдётся ни одной хорошей тройки?
б) Даны 4 различных натуральных числа. Может ли оказаться, что среди них можно найти три отличных тройки?
в) Даны 12 различных чисел (необязательно натуральных). Какое наибольшее количество отличных троек могло оказаться среди них?
Ответ: а) да; б) нет; в) 30
21. На доске было написано 30 натуральных чисел (необязательно различных), каждое из которых больше 4, но не превосходит 44. Среднее арифметическое написанных чисел равнялось 11. Вместо каждого из чисел на доске написали число, в два раза меньшее первоначального. Числа, которые после этого оказались меньше 3, с доски стёрли.
а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше 16?
б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 14, но меньше 15?
в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Ответ: а) да; б) нет; в) 20,5
22. Ученики одной школы писали тест. Результатом каждого ученика является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 85 баллов. Из-за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 7 баллов, благодаря чему количество сдавших тест увеличилось.
а) Могло ли оказаться так, что после этого средний балл участников, не сдавших тест, понизился?
б) Могло ли оказаться так, что после этого средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился?
в) Известно, что первоначально средний балл участников теста составил 85, средний балл участников, сдавших тест, составил 95, а средний балл участников, не сдавших тест, составил 70. После добавления баллов средний балл участников, сдавших тест, стал равен 100, а не сдавших тест — 72. При каком наименьшем числе участников теста возможна такая ситуация?
Ответ: а) да; б) да; в) 35
23. В одном из заданий на конкурсе бухгалтеров требуется выдать премии сотрудникам некоторого отдела на общую сумму 800 000 рублей (размер премии каждого сотрудника — целое число, кратное 1000). Бухгалтеру дают распределение премий, и он должен их выдать без сдачи и размена, имея 250 купюр по 1000 рублей и 110 купюр по 5000 рублей.
а) Удастся ли выполнить задание, если в отделе 40 сотрудников и все должны получить поровну?
б) Удастся ли выполнить задание, если ведущему специалисту надо выдать 80 000 рублей, а остальное поделить поровну на 80 сотрудников?
в) При каком наибольшем количестве сотрудников в отделе задание удастся выполнить при любом распределении размеров премий?
Ответ: а) да; б) нет; в) 63
24. На доске написано несколько различных натуральных чисел, произведение любых двух из которых больше 40 и меньше 100.
а) Может ли на доске быть 5 чисел?
б) Может ли на доске быть 6 чисел?
в) Какое наибольшее значение может принимать сумма чисел на доске, если их четыре?
Ответ: а) да; б) нет; в) 35
25. На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается их сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9; а вместо 3,3 и 5 записывается 8).
а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел.
б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7?
в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Ответ: а) пример: 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; б) нет; в) 5
26. На доске написаны числа 2 и 3. За один ход два числа a и b, записанные на доске, заменяются на два числа: или a+b и 2a−1, или a+b и 2b−1 (например, из чисел 2 и 3 можно получить либо 3 и 5, либо 5 и 5).
а) Приведите пример последовательности ходов, после которых одно из двух чисел, написанных на доске, окажется числом 19.
б) Может ли после 100 ходов одно из двух чисел, написанных на доске, оказаться числом 200?
в) Сделали 1007 ходов, причём на доске никогда не было написано одновременно двух равных чисел. Какое наименьшее значение может принимать разность большего и меньшего из полученных чисел?
Ответ: а) (2; 3), (5; 5), (10; 9), (19; 19); б) нет; в) 2
27. В последовательности 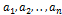 , состоящей из целых чисел
, состоящей из целых чисел 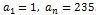
Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Ответ: а) пример: 1, 2, 3, 0, 5, -2, …,-232, 235; б) нет; в) 35
28. Множество чисел назовём хорошим, если его можно разбить на два подмножества с одинаковым произведением чисел.
а) Является ли множество 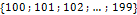 хорошим?
хорошим?
б) Является ли множество 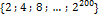 хорошим?
хорошим?
в) Сколько хороших четырёхэлементных подмножеств у множества  ?
?
Ответ: а) да; б) нет; в) 8
29. Натуральные числа a, b, c и d удовлетворяют условию a > b > c > d.
а) Найдите числа a, b, c и d, если 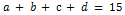 и
и 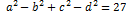 .
.
б) Может ли быть 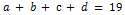 и
и 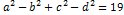 ?
?
в) Пусть 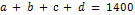 и
и 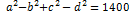 . Найдите количество возможных значений числа a.
. Найдите количество возможных значений числа a.
Ответ: а) пример: 7; 5; 2; 1; б) нет; в) 248
30. Каждое из чисел 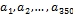 равно 1, 2, 3 или 4. Обозначим
равно 1, 2, 3 или 4. Обозначим
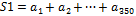
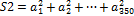
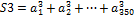
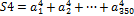
Известно, что S1 = 513.
а) Найдите S4, если еще известно, что S2 = 1097, S3 = 3243.
б) Может ли S4 = 4547?
в) Пусть S4 = 4745. Найдите все значения, которые может принимать S2.
Ответ: а) 11285; б) нет; в) 905 или 917
31. В ряд выписаны числа 12, 22,..., N2. Между ними произвольным образом расставляют знаки «+» и «-» и находят получившуюся сумму. Может ли такая сумма равняться:
а) -4, если N=12?
б) 0, если N=49?
в) 0, если N=80?
г) -3, если N=90?
Ответ: а) да; б) нет; в) да; г) да
32. а) Чему равно число способов записать число 1292 в виде 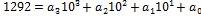 , где числа
, где числа 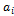 – целые,
– целые, 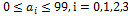 .
.
б) Существует ли 10 различных чисел N таких, что их можно представить в виде 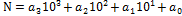 , где числа
, где числа 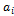 – целые,
– целые, 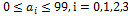 ровно 130 способами.
ровно 130 способами.
в) Сколько существует чисел N таких, что их можно представить в таком виде ровно 130 способами.
Ответ: а) 130; б) да; в) 20
33. С натуральным числом проводят следующую операцию: между каждыми двумя его соседними цифрами записывают сумму этих цифр (например, из числа 1923 получается число 110911253).
а) Приведите пример числа, из которого получается 2108124117.
б) Может ли из какого-нибудь числа получиться число 374944128?
в) Какое наибольшее число, кратное 11, может получиться из трехзначного числа?
Ответ: а) 2847; б) нет; в) 9167169
34. На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6.
б) Может ли ровно одно число на доске оканчивается на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?
Ответ: а) нет; б) нет; в) 11
35. На доске написано 30 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись заканчивается на цифру 7. Сумма написанных чисел равна 810.
а) Может ли быть 24 четных числа?
б) Может ли быть на доске ровно два числа, оканчивающихся на 7?
в) Какое наименьшее количество чисел с последней цифрой 7 может быть на доске?
Ответ: а) да; б) нет; в) 4
36. Задумано несколько натуральных чисел (не обязательно различных). Эти числа и все их возможные произведения (по 2 числа, по 3 числа и т. д.) выписывают на доску. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляют одно такое число n, а остальные числа, равные n, стирают. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 9, 12, 36.
а) Приведите пример задуманных числе, для которых на доске будет записан набор 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 3, 5, 7, 9, 15, 21, 35, 45, 105, 315, 945?
в) Приведите все примеры шести задуманных чисел, для которых на доске будет записан набор, наибольшее число в котором равно 82.
Ответ: а) 2, 3, 3, 5; б) нет; в) 1, 1, 1, 1, 1, 82 или 1, 1, 1, 1, 2, 41
37. На доске написано 100 различных натуральных чисел с суммой 5100.
а) Может ли быть записано число 250?
б) Можно ли обойтись без числа 11?
в) Какое наименьшее количество чисел, кратных 11, может быть на доске?
Ответ: а) нет; б) нет; в) 6
38. Последовательность 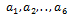 состоит из неотрицательных однозначных чисел. Пусть
состоит из неотрицательных однозначных чисел. Пусть 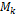 — среднее арифметическое всех членов этой последовательности, кроме k-го. Известно, что
— среднее арифметическое всех членов этой последовательности, кроме k-го. Известно, что 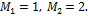
а) Приведите пример такой последовательности, для которой 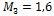 .
.
б) Существует ли такая последовательность, для которой 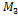 .
.
в) Найдите наименьшее возможное значение 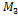 .
.
Ответ: а) пример: 5, 0, 2, 1, 1, 1; б) нет, в) 2,8
39. Две девочки делают фотографии. Наташа P фотографий, Маша K фотографий. И каждый день каждая делает на одну фотографию больше. В конце Наташа сделала на 1001 фотографию больше, чем Маша.
а) Могло ли это произойти за 7 дней?
б) Могло ли это произойти за 8 дней?
в) Максимальное количество фотографий Наташи, если Маша в последний день сделала меньше 40 фотографий.
Ответ: а) да; б) нет; в) 1430
40. Каждый из 28 студентов писал или одну из двух контрольных работ, или написал обе контрольные работы. За каждую работу можно было получить целое число баллов от 0 до 20 включительно. По каждой из двух контрольных работ в отдельности средний балл составил 15. Затем каждый студент назвал наивысший из своих баллов (если студент писал одну работу, то он назвал балл за неё). Среднее арифметическое названных баллов равно S.
а) Приведите пример, когда S<15.
б) Могло ли значение S быть равным 5?
в) Какое наименьшее значение могло принимать S, если обе контрольные работы писали 10 студентов?
Ответ: а) Пример: 14 студентов писали обе контрольные работы и получили по 20 баллов, а остальные только одну и получили по 5 баллов; б) нет; в) 185/4
41. На доске написано 30 натуральных чисел. Какие-то из красные, а какие-то зеленые. Красные числа кратны 7, а зеленые числа кратны 5. Все зеленые и красные числа отличаются друг от друга. Но между зелеными и красными могут быть одинаковые.
а) Может ли сумма зеленых чисел быть меньше 2325?
б) Может ли сумма чисел быть 1469, если только одно число красное?
в) Найдите наименьшее количество красных чисел, которое может быть при сумме 1467
Ответ: а) да; б) нет; в) 10
42. В каждой клетке квадратной таблицы 6х6 стоит натуральное число, меньшее 7. Вася в каждом столбце находит наименьшее число и складывает шесть найденных чисел. Петя в каждой строке находит наименьшее число и складывает шесть найденных чисел.
а) Может ли сумма у Пети получиться в два раза больше, чем сумма у Васи?
б) Может ли сумма у Пети получиться в шесть раз больше, чем сумма у Васи?
в) В какое наибольшее число раз сумма у Пети может быть больше, чем сумма у Васи?
Ответ: а) да; б) нет; в) 31/6
Начало формы
Конец формы
Дата добавления: 2018-11-24; просмотров: 1019; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
