Задания для самостоятельной работы
| № | Давление газа | Объем | Температура | Масса газа | Молярная масса | Газ | Количество вещ-ва | |
| °С | К | |||||||
| 1 | 1 .105 | 50 | 27 | Н2 | ||||
| 2 | 2.105 | 280 | О2 | 4 | ||||
| 3 | 100 | 20 | 220 | 0,044 | ||||
| 4 | 5.105 | 4 | 0,004 | 2 | ||||
| 5 | 1,3.105 | 240 | 250 | 30 | ||||
| 6 | 1 .104 | 4 | -32,4 | 0,032 | ||||
| 7 | 8,3.104 | 300 | 0,002 | 5 | ||||
| 8 | 15 | 17 | СО2 | 0,5 | ||||
| 9 | 1 .105 | 126 | 100 | Н2О | ||||
| 10 | 40 | 7 | 80 | 2,5 | ||||
| № | Давление газа | Объем | Температура | Масса газа | Молярная масса | Газ | Количество вещ-ва | |
| °С | К | |||||||
| 1 | 1 .105 | 50 | 27 | Н2 | ||||
| 2 | 2.105 | 280 | О2 | 4 | ||||
| 3 | 100 | 20 | 220 | 0,044 | ||||
| 4 | 5.105 | 4 | 0,004 | 2 | ||||
| 5 | 1,3.105 | 240 | 250 | 30 | ||||
| 6 | 1 .104 | 4 | -32,4 | 0,032 | ||||
| 7 | 8,3.104 | 300 | 0,002 | 5 | ||||
| 8 | 15 | 17 | СО2 | 0,5 | ||||
| 9 | 1 .105 | 126 | 100 | Н2О | ||||
| 10 | 40 | 7 | 80 | 2,5 | ||||
Решить задачи, определяя неизвестные величины и заполняя таблицу
Литература:
1 Дмитриева В.Ф., Физика для профессий и специальностей технического профиля: учебник для образовательных учреждений начального и среднего профессионального образования,/ В.Ф. Дмитриева – М.: 2014 450с.
|
|
|
2 Дмитриева В.Ф., Физика: учебник для студентов образовательных учреждений среднего профессионального образования,/ В.Ф. Дмитриева – М.: 2012 135с.
3 Дмитриева В.Ф., Физика для профессий и специальностей технического профиля. Сборник задач: учебное пособие для образовательных учреждений начального и среднего профессионального образования – М.: 2014 450с.
4 Дмитриева В.Ф., Физика для профессий и специальностей технического профиля. Сборник задач: учебное пособие для образовательных учреждений начального и среднегопрофессиональногообразования – М.: 2013 320с.
Практическое занятие №8
По теме «Свойства паров (газов), жидкости и твердых тел»
Цель: ввести представление о силе поверхностного натяжения; дать энергетическую трактовку коэффициента поверхностного натяжения;
рассмотреть вопрос о давлении под искривленной поверхностью жидкости;
Объяснить явления смачивания и несмачивания; выяснить природу капиллярных явлений.
Теория:
¾ Давление насыщенного пара
¾ Давление насыщенного пара (p0) не зависит от объёма, а зависит от температуры (T) и концентрации молекул пара (n) 
, где k – постоянная Больцмана СИ: Па
|
|
|
¾ Относительная влажность воздуха
Относительной влажностью воздуха (φ) называют отношение парциального давления (р) водяного пара, содержащегося в воздухе при данной температуре, к давлению (р0) насыщенного пара при той же температуре, выраженной в процентах. 
% СИ: %
¾ Абсолютная влажность воздуха
Абсолютная влажность воздуха (ρ):
1 давление, оказываемое водяным паром при данных условиях: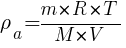 
;
2 это масса (m) водяного пара в единице объёма (V = 1 м3) воздуха: 
;
СИ: Па, кг/м3
¾ Коэффициент поверхностного натяжения жидкости
¾ Коэффициент поверхностного натяжения (σ) жидкости равен отношению модуля силы поверхностного натяжения (F) к длине (l) границы поверхности натяжения, на которую действует эта сила. 
СИ: Н/м
¾ Высота поднятия жидкости в капилляре
¾ Высота (h) поднятия жидкости в капиллярной трубке (капилляре) прямо пропорциональна коэффициенту поверхностного натяжения (σ) и обратно пропорциональна плотности жидкости (ρ) и радиусу (r) капиллярной трубки.
¾ Капиллярное давление
¾ Капиллярное давление (p) жидкости в капилляре пропорционально коэффициенту поверхностного натяжения (σ) и обратно пропорционально радиусу капиллярной трубки (r). 
СИ: Па
|
|
|
¾ Абсолютная деформация (удлинение — сжатие)
¾ Абсолютная деформация (Δl) — разность линейных размеров (l0 и l) твердого тела до и после приложения к нему силы.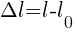 
. СИ: мм
¾ Относительная деформация (удлинение — сжатие)
¾ Относительная деформация (ε) — отношение абсолютной деформации (Δl) к начальной длине твердого тела (l0).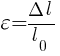 
¾ Механическое напряжение
¾ Механическое напряжение (σ) — это отношение модуля силы упругости (F) к площади поперечного сечения (S) тела. 
. СИ: Па
¾ Закон Гука для твердого тела
¾ При малых деформациях напряжение (σ) прямо пропорционально относительному удлинению (ε)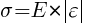 
. СИ: Па
¾ Модуль упругости (модуль Юнга)
¾ Модуль продольной упругости (Е) — постоянная для данного материала величина, численно равная механическому напряжению (σ), которое необходимо создать в теле, чтобы его относительное удлинение (ε) достигло единицы 
. СИ: Па
|
|
|
¾ Коэффициент запаса прочности
¾ Коэффициент запаса прочности (n) — это величина, показывающая во сколько раз напряжение (σпч), соответствующее пределу прочности, превышает напряжение (σдоп), допустимое для твердого тела в данных условиях нагрузки n=σпч/σдоп..
Задача 1. В калориметр, который содержит 400 г воды при 17 °C, пускают 10 г пара, температура которого 100 °C. Какая температура установилась в калориметре?
| Дано: t1 = 17 °C m1 = 400 г t2 = 100 °C m2 = 10 г | Решение: Вода в калориметре нагревается до температуры t за счет теплоты, которую отдает сконденсированный пар, и теплоты вследствие охлаждения образованной из нее воды: cВm1(t — t1) = rm2 + cВm2(t2 — t). Осуществив определенные математические преобразования, получим: t = (rm2 + cВm2t2 + cВm1t1) / cВ(m1 + m2); t = 32 °C. |
| t — ? | Ответ: t = 32 °C. |
Задача 2. В пустой сосуд объемом 1 м3 налили 10 г воды при 20 °C и плотно закрыли. Будет ли в нем пар насыщенным? Какое минимальное количество воды надо налить, чтобы пар стал насыщенным?
| Дано: T = 273 K m = 10 г V = 1 м3 | Решение: Из уравнения Менделеева-Клапейрона pV = (m / M) • RT определим давление, которое установилось после испарения воды: p = 1351 Па. В таблице находим давление насыщенного водяного пара при 20 °C: pн = 2333 Па. Если в уравнение Менделеева-Клапейрона подставить значение давления насыщенного пара, то получим минимальное количество воды, которую нужно испарить, чтобы пар стал насыщенным: m0 = pнVM / RT = 17,3 г. |
| p — ?, m0 — ? | Ответ: p = 1351 Па, m0 = 17,3 г. |
Задача 3. Водяной пар, который находится в закрытом сосуде объёмом 5,76 л при 15 °C, оказывает давление 1280 Па. Каким будет его давление, если объем увеличится до 8 л, а температура повысится до 27 °C?
| Дано: t1 = 15 °C V1 = 5,76 л p1 = 1280 Па t2 = 27 °C V2 = 8 л | Решение: Из таблицы давление насыщенного водяного пара при 15 °C pн = 1710 Па. Следовательно, пар ненасыщенный. Для 27 °C pн = 3559 Па. Согласно уравнению состояния идеального газа p1V1 / T1 = p2V2 / T2; p2 = 960 Па. |
| p2 — ? | Ответ: p2 = 960 Па. |
Задача 4. Алюминиевая деталь массой 560 г была нагрета до 200 °C и затем брошена в воду, температура которой 16 °C. При этом часть воды испарилась, а та часть, которая осталась, нагрелась до 50 °C. Сколько воды испарилось? Начальная масса воды 400 г.
| Дано: tа = 200 °C mа = 560 г tв = 16 °C mВ = 400 г t = 50 °C | Решение: В результате охлаждения алюминиевой детали выделилось количество теплоты Q4, которое затрачено на испарение части воды (Q2 + Q3) и нагревание оставшейся воды Q1. Q1 = (mВ — mП)cВ(t — tВ); Q2 = cВmП(100 °C — tВ); Q3 = rmП; Q4 = cаmа(tа — t); Q4 = Q1 + Q2 + Q3. cаmа(tа — t) = cВmВ(t — tВ) — cВmП(t — tВ) + cВmП(100 °C — tВ) + rmП. Решив это уравнение относительно неизвестного mП, получим: mП = 6,7 • 10-3 кг. |
| mП — ? | Ответ: mП = 6,7 • 10-3 кг. |
Задача 5. В железном баке массой 5 кг находится 20 кг воды и 6 кг льда при 0 °C. Сколько водяного пара температурой 100 °C надо впустить в бак, чтобы растопить лед и нагреть воду до 70 °C?
| Дано: t1 = 0 °C mЛ = 6 кг mб = 5 кг mВ = 20 кг t = 70 °C | Решение: В результате конденсации пара и охлаждения образовавшейся воды выделилось количество теплоты Q1 + Q2. По условию теплового баланса оно затрачено на плавление льда Q3, нагревание образовавшейся воды Q4 и находящейся в баке воды Q5, а также на нагревание самого бака Q6. Q1 = rmП; Q2 = cВmП(tП — t); Q2 = cВmП(100 °C — tВ); Q3 = λmЛ; Q4 = cВmЛ(t — 0 °C); Q5 = cВmВ(t — 0 °C); Q6 = cжmб(t — 0 °C). Q1 + Q2 = Q3 + Q4 + O5 + Q6. Решив это уравнение относительно неизвестного mП, получим: mП = 4 кг. |
| mП — ? | Ответ: mП = 4 кг. |
Задача 6. Относительная влажность воздуха в комнате при 25 °C составляет 70%. Сколько воды конденсируется из каждого кубометра воздуха в случае снижения температуры до 16 °C?
| Дано: t1 = 25 °C φ = 70% t2 = 16 °C | Решение: φ = (ρ / ρн) • 100%. Из таблицы плотность насыщенного пара при 25 °C равна pН1 = 23 • 10-3 кг/м3. Следовательно, ρ = φρН1 = 16,1 • 10-3 кг/м3. Точка росы для данной абсолютной влажности воздуха равна tр = 19 °C, поэтому влага начнет конденсироваться при температуре ниже точки росы, т. е. от 19 °C до 16 °C. Поскольку ρ = m / V, то m1 = ρV, a m2 = ρН2V. Из таблицы устанавливаем, что для 16 °C плотность насыщенного водяного пара равна ρН2 = 13,6 • 10-3 кг/м3. Следовательно, mВ = m1 — m2 = ρV — ρН2V; mВ = (16,1 • 10-3 кг/м3 — 13,6 • 10-3 кг/м3) • 1 м3 = 2,5 • 10-3 кг. |
| mВ — ? | Ответ: mВ = 2,5 • 10-3 кг. |
Задача 7. Поверхностное натяжение жидкости можно определить экспериментально с помощью чувствительного динамометра и кольца из проволоки: кольцо опускают на поверхность воды, а затем отрывают его от нее, фиксируя с помощью динамометра силу в момент отрыва (рис. 3.17). Водном из таких опытов использовалось алюминиевое кольцо диаметром 20 см и массой 5,7 г; в момент отрыва динамометр показал 0,15 Н. По этим данным вычислите поверхностное натяжение воды.
Дата добавления: 2018-11-24; просмотров: 780; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!