Задания для самостоятельного решения
1.Камень массой 0,2 кг бросили под углом 600 к горизонту со скоростью 15 м/с. Найти кинетическую, потенциальную и полную энергию камня: а) спустя 1 с после начала движения; б) в высшей точке траектории. Сопротивлением воздуха пренебречь.
2.Тело массой 5 кг падает с высоты 20 м. Определить полную энергию тела в точке, находящейся от поверхности Земли на высоте 5 м. Трением тела о воздух пренебречь. Сравнить эту энергию с первоначальной энергией тела.
3.Тело, падая с некоторой высоты, в момент соприкосновения с Землей обладает импульсом 100 кг·м/с и кинетической энергией 500 Дж. Определить: а) с какой высоты тело падало; б) массу тела.
4.Тело брошено под углом 450 к горизонту со скоростью v 0 =15 м/с. Используя закон сохранения энергии, определить скорость тела в высшей точке его траектории.
5. Мальчик везёт санки с постоянной скоростью. Сила трения санок о снег равна 30 Н. Мальчик совершил работу, равную 30 Дж. Определите пройденный путь.
6.При открывании двери пружину жёсткостью 50 кН/м растягивают на 10 см. Какую работу совершает пружина, открывая дверь?
7. Вагон массой 20 т, движущийся со скоростью 0,3 м/с. Догоняет вагон массой 30 т, движущийся со скоростью 0.2 м/с. Найдите скорость вагонов после их взаимодействия, если удар неупругий.
8. Пуля массой 10 г попадает в деревянный брусок, лежащий на гладкой поверхности, и застревает в нём. Скорость бруска после этого становится равной 8 м/с. Масса бруска в 49 раз больше массы пули. Определите скорость пули до попадания в брусок.
|
|
|
9. Спортсмен поднимает гирю массой 16 кг на высоту 2 м, затрачивая на это 0,8 с. Какую мощность при этом развивает спортсмен?
10.Тело массой 100г движется по окружности со скоростью 0,4 м/с. Определите модуль изменения импульса за половину периода.
Литература:
1 Дмитриева В.Ф., Физика для профессий и специальностей технического профиля: учебник для образовательных учреждений начального и среднего профессионального образования,/ В.Ф. Дмитриева – М.: 2014 - 450с.
2 Дмитриева В.Ф., Физика: учебник для студентов образовательных учреждений среднего профессионального образования,/ В.Ф. Дмитриева – М.: 2012 - 135с.
3 Дмитриева В.Ф., Физика для профессий и специальностей технического профиля. Сборник задач: учебное пособие для образовательных учреждений начального и среднего профессионального образования – М.: 2014 - 450с.
4 Дмитриева В.Ф., Физика для профессий и специальностей технического профиля. Сборник задач: учебное пособие для образовательных учреждений начального и среднего профессионального образования – М.: 2013 - 320с.
Практическое занятие №5
По теме «Колебания и волны. Определение амплитуды, периода, частоты по графику колебаний»
|
|
|
Цель: Закрепить знания по теме «Колебания и волны», сформировать умения и навыки нахождения физической величины, её вывода из формулы.
| Теория: | |||||||
| Колебания, рассматриваемые в разделе «Механика», называются механическими, при которых рассматриваются изменения положений, скоростей, ускорений и энергий каких-либо тел или их частей. Силу, под действием которой происходит колебательный процесс, называют возвращающей силой.
Простейшим видом периодических колебаний являются гармонические колебания, происходящие по закону синуса или косинуса. Гармоническая колебательная система (система тел, совершающих колебания) обычно имеет одно положение, в котором может пребывать сколь угодно долго – положение равновесия О.
Отклонения от положения равновесия называют смещением, и обозначается Х, а наибольшее смещение (точки В или С) называется амплитудой колебания и обозначается А. Периодические колебания совершаются циклично. Движение в течение одного цикла (когда тело, пройдя все промежуточные положения, возвращается в исходное) называется полным колебанием (О-С-О-В-О). Время одного полного колебания называется периодом колебания (обозначается Т). Если тело за время t совершает n полных колебаний то
Математическая запись гармонического колебания: где Простейшими колебательными системами являются: а) математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания под действием силы тяжести. Период колебания определяется уравнением: Период Т зависит лишь от длины маятника и местоположения (удалённости от центра Земли или другого небесного тела), которое определяется величиной ускорения свободного падения б) пружинный маятник – материальная точка, закреплённая на абсолютно упругой пружине. Период колебания определяется уравнением:
Задача 1
 Мы поможем в написании ваших работ! | |||||||
, а 
и называется частотой колебаний. Число колебаний за 2π единиц времени называется циклической (круговой) частотой и обозначается ω: 
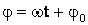– фаза колебания (физическая величина, определяющая положение колебательной системы в данный момент времени),φ0 – начальная фаза колебания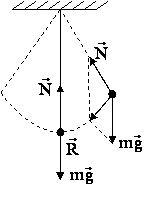 
.
;
.
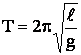