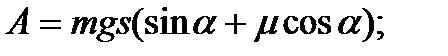По теме « Потенциальная и кинетическая энергия. Законы сохранения в механике. Работа и мощность »
Цель: Закрепить знания по теме «Законы сохранения в механике», сформировать умения и навыки нахождения физической величины, её вывода из формулы.На примере конкретных задач рассмотреть понятия работы, потенциальной кинетической энергии; проанализировать границы применимости законов сохранения на конкретных примерах.
Теория:
1. Работа и мощность
Когда под действием некоторой силы тело совершает перемещение, то действие силы характеризуется величиной, которая называется механической работой.
Механическая работа- мера действия силы, в результате которого тела совершают  перемещение.
перемещение.
Работа постоянной силы.Если тело движется прямолинейно под действием постоянной силы  , составляющей некоторый уголaс направлением перемещения
, составляющей некоторый уголaс направлением перемещения  (рис.1), работа равна произведению этой силы на перемещение точки приложения силы и на косинус углаaмежду векторами и
(рис.1), работа равна произведению этой силы на перемещение точки приложения силы и на косинус углаaмежду векторами и  ; или работа равна скалярному произведению вектора силы на вектор перемещения:
; или работа равна скалярному произведению вектора силы на вектор перемещения:
 .
.
1 Дж - работа, совершаемая силой в 1Н при перемещении на 1м в направлении действия силы.
1. если a- острый угол,  ,
, 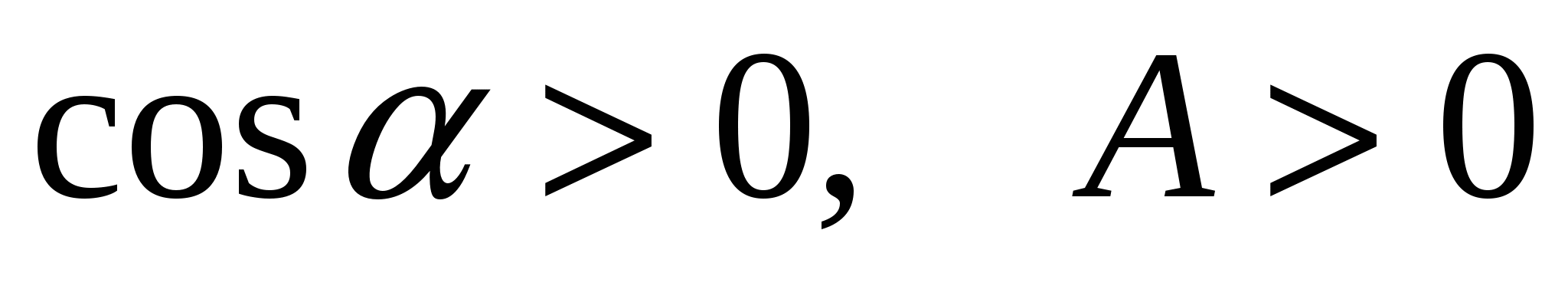 ;
;
2. если a- тупой угол,  ,
,  ;
;
3. если 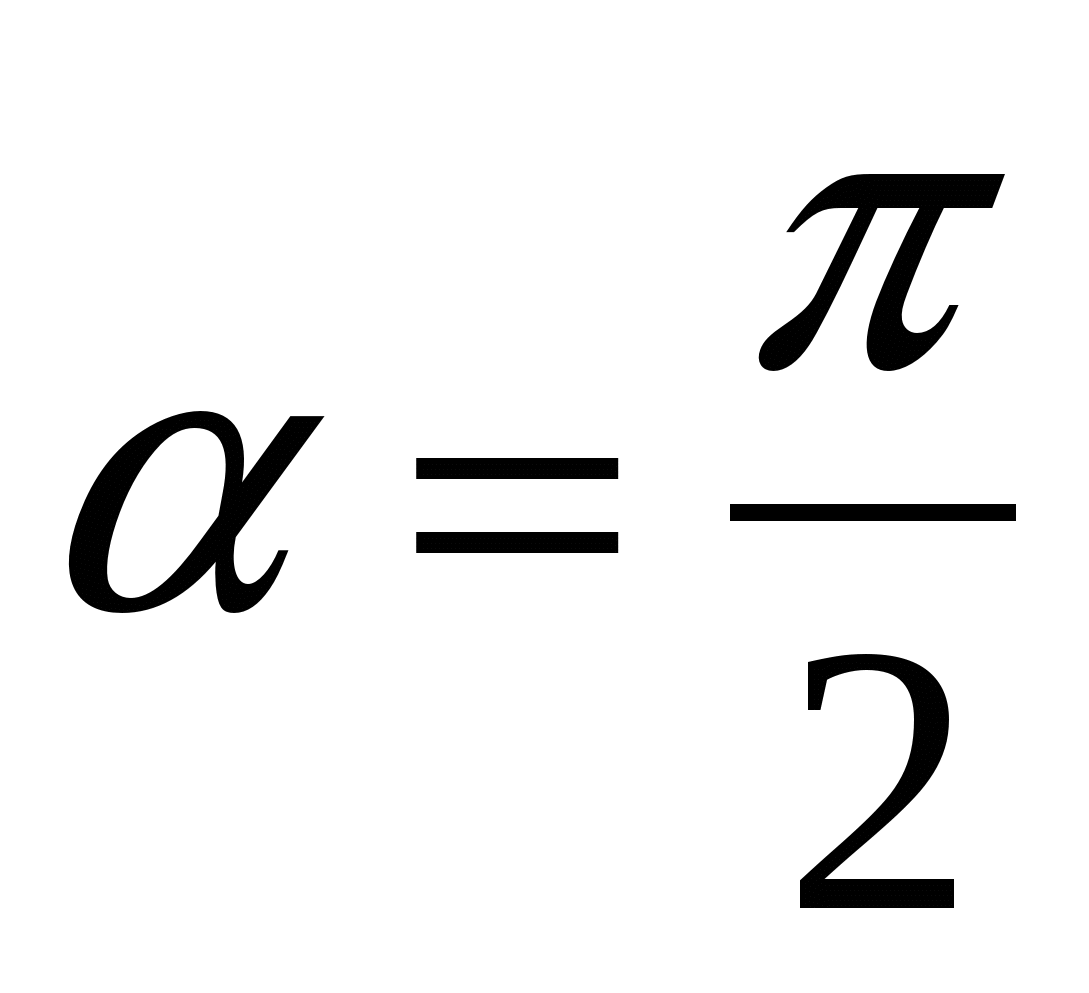 ,
,  .
.


Если начальная деформация x1=0, то 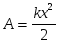 .
.
При сжатии пружины совершается такая же работа.
Г 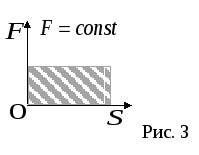
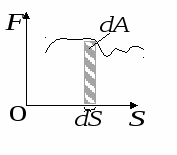 рафическое изображение работы (рис.3).
рафическое изображение работы (рис.3).
На графиках работа численно равна площади заштрихованных фигур.
Для характеристики быстроты совершения работы вводят понятие мощности.
Мощность постоянной силы численно равна работе, совершаемой этой силой за единицу времени.
|
|
|
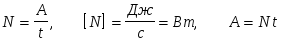 .
.
1 Вт- это мощность силы, которая за 1 с совершает 1 Дж работы.
В случае переменной мощности (за малые одинаковые промежутки времени совершается различная работа) вводится понятие мгновенной мощности:
 ,
,
где  скорость точки приложения силы.
скорость точки приложения силы.
Т.о. мощность равна скалярному произведению силы на скорость  точки её приложения.
точки её приложения.
Энергия. Потенциальная и кинетическая энергия. Закон сохранения энергии.
Все введенные ранее величины характеризовали только механическое движение. Однако форм движения материи много, постоянно происходит переход от одной формы движения к другой. Необходимо ввести физическую величину, характеризующую движение материи во всех формах её существования, с помощью которой можно было бы количественно сравнивать различные формы движения материи.
Энергия- мера движения материи во всех её формах. Основное свойство всех видов энергии - взаимопревращаемость. Запас энергии, которой обладает тело, определяется той максимальной работой, которую тело может совершать, израсходовав свою энергию полностью. Энергия численно равна максимальной работе, которую тело может совершить, и измеряется в тех же единицах, что и работа. При переходе энергии из одного вида в другой нужно подсчитать энергию тела или системы до и после перехода и взять их разность. Эту разность принято называтьработой:  .
.
|
|
|
Т. о., физическая величина, характеризующая способность тела совершать работу, называется энергией.
Механическая энергия тела может быть обусловлена либо движением тела с некоторой скоростью, либо нахождением тела в потенциальном поле сил.
Кинетическая энергия.
Энергия, которой обладает тело вследствие своего движения, называется кинетической. Работа, совершенная над телом, равна приращению его кинетической энергии.
Найдем эту работу для случая, когда равнодействующая всех приложенных к телу сил равна 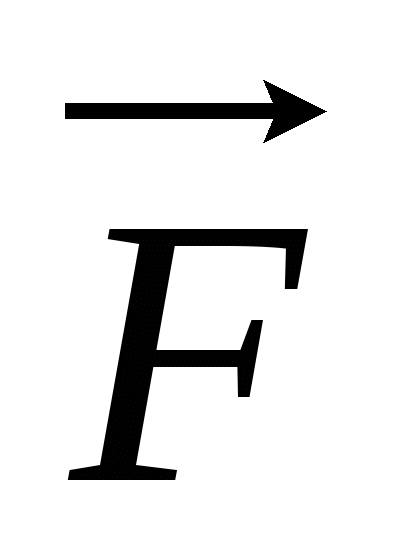 .
.
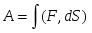 ,
,


Работа, совершенная телом за счет кинетической энергии, равна убыли этой энергии.
Потенциальная энергия.
Если в каждой точке пространства на тело воздействуют другие тела с силой, величина которой может быть различна в разных точках, говорят, что тело находится в поле сил или силовом поле.
Если линии действия всех этих сил проходит через одну точку - силовой центр поля, - а величина силы зависит только от расстояния до этого центра, то такие силы называются центральными, а поле таких сил - центральным (гравитационное, электрическое поле точечного заряда).
|
|
|
Поле постоянных во времени сил называется стационарным.
Поле, в котором линии действия сил - параллельные прямые, расположенные на одинаковом расстоянии друг от друга - однородное.
Все силы в механике подразделяются на консервативные и неконсервативные (или диссипативные).
Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положением тела в пространстве, называются консервативными.
Работа консервативных сил по замкнутому пути равна нулю. Все центральные силы являются консервативными. Силы упругой деформации также являются консервативными силами. Если в поле действуют только консервативные силы, поле называется потенциальными (гравитационные поля).
Силы, работа которых зависит от формы пути, называются неконсервативными (силы трения).
Потенциальной энергией называют часть общей механической энергии системы, которая определяется только взаимным расположением тел, составляющих систему, и характером сил взаимодействия между ними. Потенциальная энергия- это энергия, которой обладают тела или части тела вследствие их взаимного расположения.
|
|
|
Понятие потенциальной энергии вводится следующим образом. Если тело находится в потенциальном поле сил (например, в гравитационном поле Земли), каждой точке поля можно сопоставить некоторую функцию (называемую потенциальной энергией) так, чтобы работа А12, совершаемая над телом силами поля при его перемещении из произвольного положения 1 в другое произвольное положение 2, была равна убыли этой функции на пути 1®2:
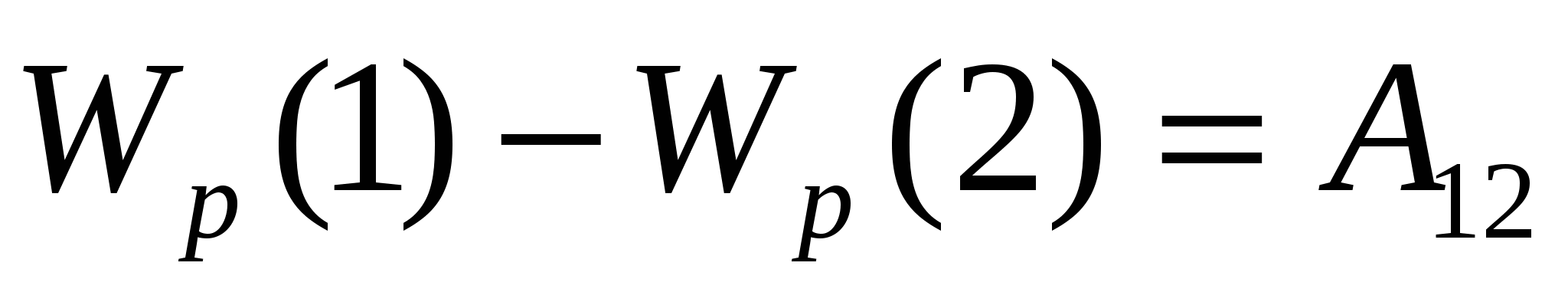 ,
,
где  и
и  значения потенциальной энергии системы в положениях 1 и 2.
значения потенциальной энергии системы в положениях 1 и 2.

Записанное соотношение позволяет определить значение потенциальной энергии с точностью до некоторой неизвестной аддитивной постоянной. Однако, это обстоятельство не имеет никакого значения, т.к. во все соотношения входит только разность потенциальных энергий, соответствующих двум положениям тела. В каждой конкретной задаче уславливаются считать потенциальную энергию какого-то определенного положения тела равной нулю, а энергию других положений брать по отношению к нулевому уровню. Конкретный вид функции  зависит от характера силового поля и выбора нулевого уровня. Поскольку нулевой уровень выбирается произвольно, может иметь отрицательные значения. Например, если принять за нуль потенциальную энергию тела, находящегося на поверхности Земли, то в поле сил тяжести вблизи земной поверхности потенциальная энергия тела массойm, поднятого на высотуhнад поверхностью, равна
зависит от характера силового поля и выбора нулевого уровня. Поскольку нулевой уровень выбирается произвольно, может иметь отрицательные значения. Например, если принять за нуль потенциальную энергию тела, находящегося на поверхности Земли, то в поле сил тяжести вблизи земной поверхности потенциальная энергия тела массойm, поднятого на высотуhнад поверхностью, равна 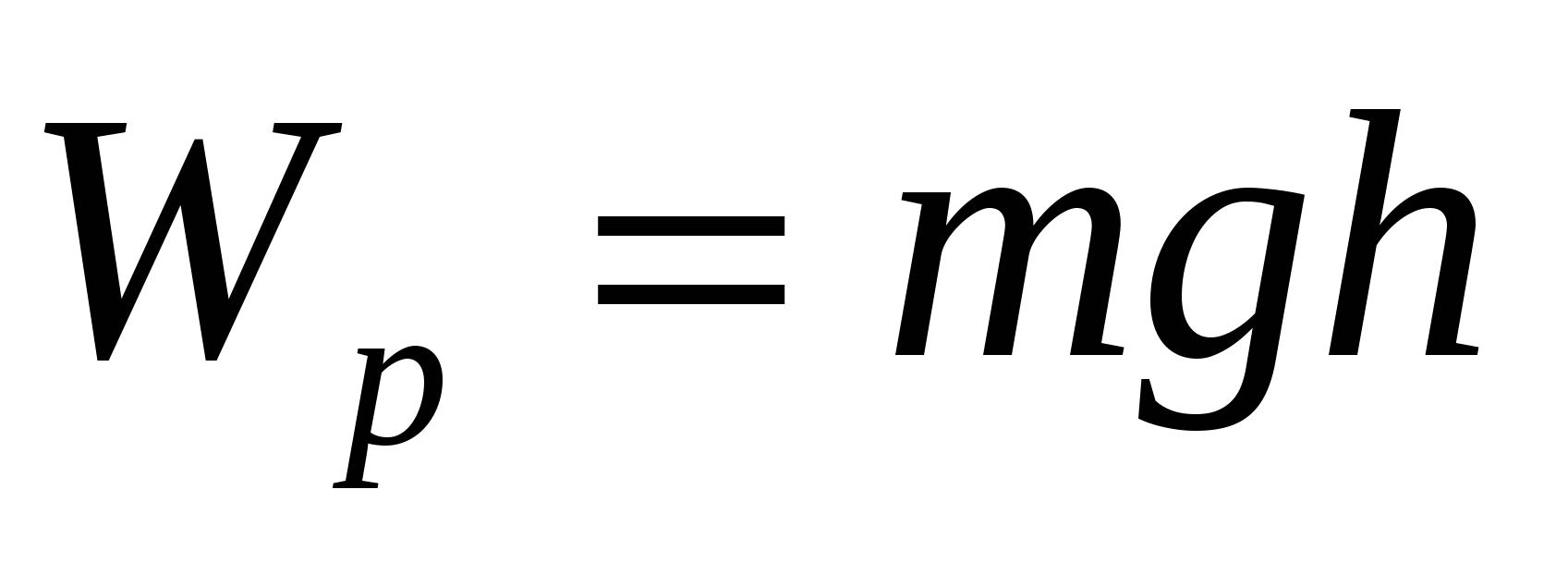 (рис. 5).
(рис. 5).

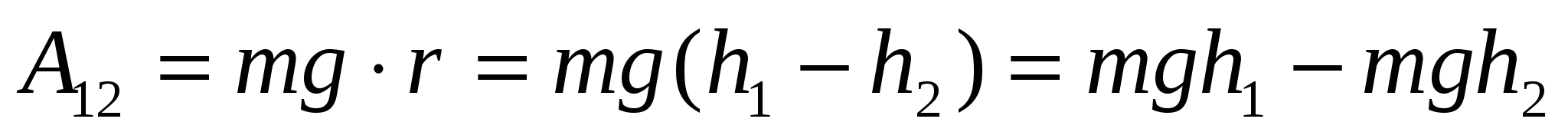 ,
,
где  - перемещение тела под действием силы тяжести; при
- перемещение тела под действием силы тяжести; при  ,
,
Потенциальная энергия этого же тела, лежащего на дне ямы глубиной H, равна
 .
.
В рассмотренном примере речь шла о потенциальной энергии системы Земля-тело.
Потенциальной энергией может обладать не только система взаимодействующих тел, но отдельно взятое тело. В этом случае потенциальная энергия зависит от взаимного расположения частей тела.
Выразим потенциальную энергию упруго деформированного тела.

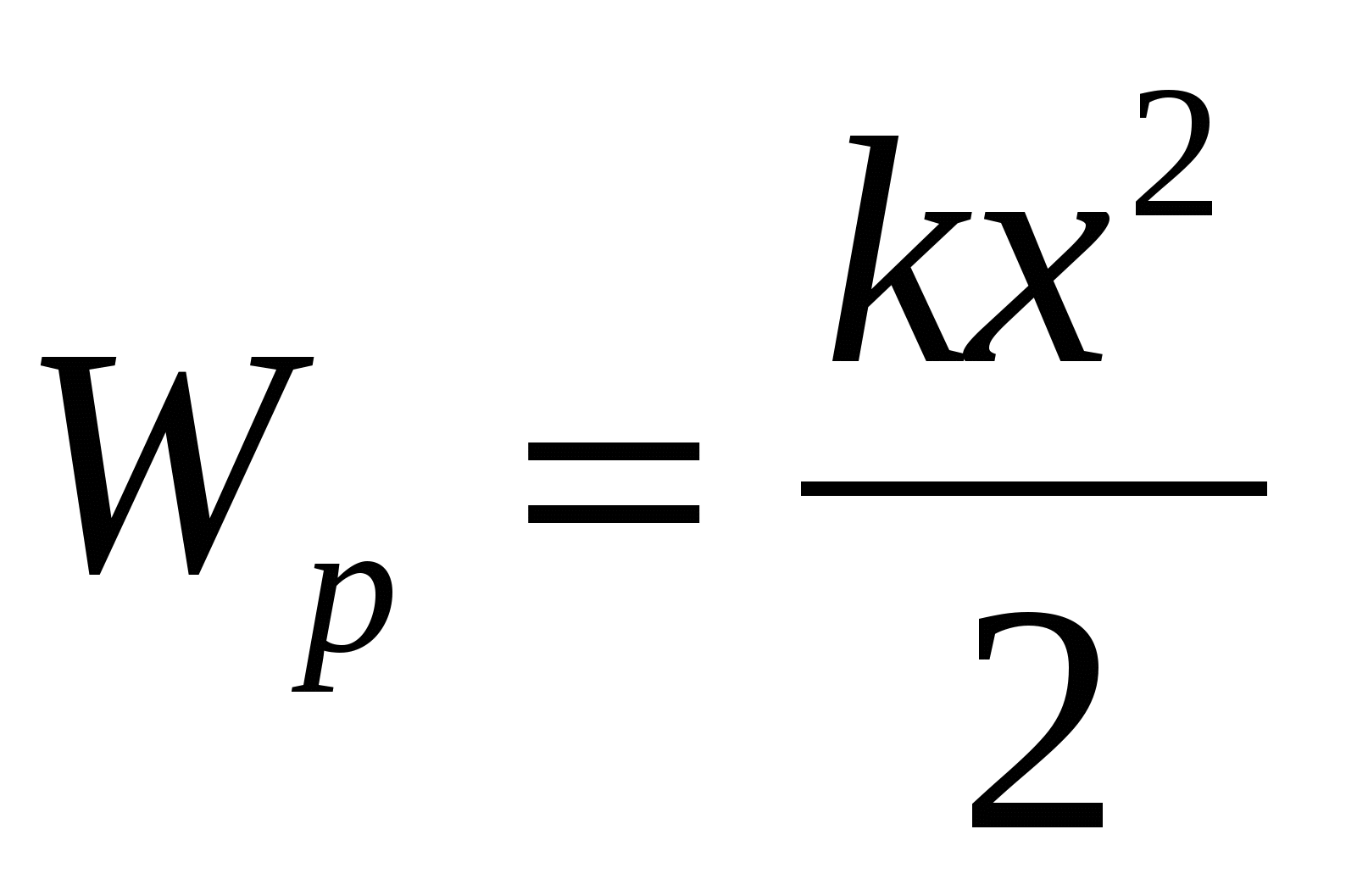 - потенциальная энергия упругой деформации, если принять, что потенциальная энергия недеформированного тела равна нулю;
- потенциальная энергия упругой деформации, если принять, что потенциальная энергия недеформированного тела равна нулю;
где k- коэффициент упругости,x- деформация тела.
В общем случае тело одновременно может обладать и кинетической и потенциальной энергиями. Сумма этих энергий называется полной механической энергией тела: 
Полная механическая энергия системы равна сумме её кинетической и потенциальной энергий. Полная энергия системы равна сумме всех видов энергии, которыми обладает система.
Закон сохранения энергии - результат обобщения многих экспериментальных данных. Идея этого закона принадлежит Ломоносову, изложившему закон сохранения материи и движения, а количественная формулировка дана немецким врачом Майером и естествоиспытателем Гельмгольцем.
Законсохранения механической энергии:в поле только консервативных сил полная механическая энергия остается постоянной в изолированной системе тел. Наличие диссипативных сил (сил трения) приводит к диссипации (рассеянию) энергии, т.е. превращению её в другие виды энергии и нарушению закона сохранения механической энергии.
Закон сохранения и превращения полной энергии:полная энергия изолированной системы есть величина постоянная.
Энергия никогда не исчезает и не появляется вновь, а лишь превращается из одного вида в другой в эквивалентных количествах. В этом и заключается физическая сущность закона сохранения и превращения энергии: неуничтожимость материи и её движения.
Задача 1. С башни высотой 20 м горизонтально со скоростью 10 м/с брошен камень массой 400 г (рис. 1). Пренебрегая сопротивлением воздуха, определить кинетическую и потенциальную энергию камня через 1 с после начала движения.
Дано: H = 20 м; v 0 = 10 м/с; m = 0,4 кг; t = 1c.
Найти: Ek , E п. Решение: В точке А Подставляя числовые данные, получим Ek = 39,2 Дж, E п = 59,2 Дж. Ответ: Ek = 39,2 Дж, E п = 59,2 Дж
Задача 2. Автомобиль массой 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути (рис. 2). Определить: а) работу, совершаемую двигателем автомобиля на пути 5 км, если коэффициент трения равен 0,1; б) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин. Дано: m = 1800 кг; sinα = 0,03; s = 5000 м; μ = 0,1; t = 300 с. Найти: А, Р. Решение:
  где где  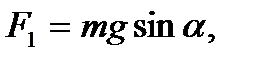
Подставляя числовые данные, получим: А = 11,5·106 Дж, Р = 38,3·103 Вт. Ответ: А = 11,5 МДж, Р = 38,3кВт.
 Мы поможем в написании ваших работ! |

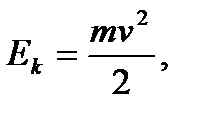
 где
где