Годовое изменение параметров Земли 21 страница
Из формулы Лебедева следует, что длина волны эфира (вакуума) изменяется при переходе из одной области пространства атома в другую (т.е. при изменении радиуса орбиты электрона). И это изменение есть следствие соответствующего изменения плотности пространства, сопровождающееся пропорциональным изменением как орбитальной скорости электрона, так и скорости света с разницей, равной постоянной тонкой структуры a . И, следовательно, фотоны, движущиеся вблизи поверхности ядра атома (например, на расстоянии а – 10-14 см) будут иметь скорость большую, чем скорость в вакууме. Покажем это:
аv2 =0,529·10-8·(2,188·108) = 2,53·108 = Å,
отсюда:
с = a Ö(Å / a ') = 137,04Ö2,53·108/10-14 = 2·1012 см/сек.
Скорость света вблизи поверхности ядра 20 млн. км/сек. и превышает ее же в эфире на два порядка. Это превышение может быть зарегистрировано различными приборами (например, на синхрофазотроне) и не фиксировалась она только потому, что такая скорость запрещена постулативно и никто не пытался поставить эксперимента по проверке постулата. (Имеется информация, что еще большая скорость – 90 млн. км/сек зарегистрирована учеными Принстонского университета в 2000 г.)
Поскольку уравнение расчета длины волны вакуума одно для всех элементов и их изотопов то можно предположить, что каждый элемент и изотоп имеют свой радиус боровской орбиты и вычислить его по (6.23) для RН, RД, RТ:
аН = 1/4a p Rн = 5,2946544·10-9 см;
аД = 5,2932151·10-9 см;
|
|
|
аТ = 5,2927278·10-9 см.
Таким образом, радиус атома водорода ан = 5,2946544·10-9 см уже в четвертом знаке отличается от теоретического радиуса первой боровской орбиты аb = 5,291775·10-9 см, а, следовательно, и находящийся на этой орбите электрон будет иметь иную величину параметров, включая скорость его движения по орбите.
Так как величина радиусов боровской орбиты водорода и его изотопов различна, то и радиусы орбит электронов и их параметры, так же как и усредненные параметры радиусов ядер, будут различными. Зная, что поверхность ядра водорода лежит на расстоянии к65 от «первого» радиуса, определим радиус ядер данных элементов:
rн = 1,5904537·10-15см;
rд = 1,5900213·10-15 см;
rт = 1,5898751·10-15см.
Естественно, что это усредненные, чисто теоретические радиусы. Аналогично можно вычислить и пространственное распределение электронных орбит в атоме и по ним рассчитать переходы электронов с орбиты на орбиту и спектральные длины волн испускаемых фотонов. Однако для нахождения этих длин радиусы орбит определять не обязательно. Можно обойтись и без уравнения [142], определяющего длину спектральных линий:
l/l 21 = R ¥(1/n12 - 1/n22). (6.24)
Это уравнение получено из условия целочисленного квантования и отображает испускание фотонов электронами не со всех электронных орбит, а только с части их, начиная с некоторой случайной 1. И например, у водорода эмпирически фиксируется, почти на порядок больше спектральных линий, чем то количество, которое объясняется теоретически.
|
|
|
Поскольку уравнение (6.16) определяет пошаговый порядок вычисления спектральных линий каждого элемента, а длина шага, есть половина длины стоячей волны, образуемой атомом, то и количество спектральных линий, которые могут быть испущены каждым элементом таблицы Менделеева, исчисляется от многих тысяч до десятков тысяч. Фактически наблюдается только некоторая часть из них. Это вызвано тем, что большая часть спектра испускания находится в глубоком ультрафиолете, другая часть еще не отождествляется с элементами, которыми она испускается, третья испускается изотопами и не отделена от линий, испускаемых элементами (так, например, в водородной серии Лаймана присутствует линия дейтерия. А серии Бальмера, Пашена и последующие, похоже, водородом не испускаются). И главное ¾ сами спектральные линии испускаются элементами во множестве физических взаимодействий, а приборно замеряются с точной фик сацией элемента испускания всего несколько видов (в пламени, разрядный, искровой, вероятно плазменный, от звезд ¾ вот, пожалуй, и все) и в очень узкой полосе разрежения, в основном атмосферного. Наконец, от сутствует теория построения структуры испускания спектральных линий элементами, а существующая квантовая модель не может считаться удовлетворительной уже потому, что не обеспечивает расчета спектральных линий даже такого всесторонне изучен ного элемента, как водород.
|
|
|
Рассмотрим возможность построения структуры спектральных линий водорода не квантовыми методами. Рассмотрение начнем с анализа структуры наиболее известных серий спектральных линий водорода: серий Лаймона, Бальмера, Пашена, Брекета и Пфунда. Серий эти являются в некоторой степени классическими, поскольку рассчитываются методами квантовой механики по обобщенной формуле [148]:
w = R ¥(1/m2 - 1/n2), (6.25)
где w - частота излучаемого фотона, R ¥ - «постоянная» Ридберга, m - 1, 2, 3,..., п - т + 1.
И считается, что полученные по формуле (6.25) спектральные линии относятся именно к водороду, охватывают все его линии, а сами серии являются как бы спектроотображением наличия водорода в структуре того элемента, в котором встречается хотя бы несколько линий данных серий. К тому же все они давно уже зафиксированы спектроскопическими методами.
|
|
|
И все же есть достаточно веские основания для сомнения в истинности таких представлений. Можно показать теоретически, что многие линии данных спектров (кроме линий серии Лаймана) не входят в структуру системы линий, образуемых в результате испускания фотонов атомом водорода. Построим таблицу всех пяти спектральных линий водорода (табл. 26) с использованием коэффициента Ридберга R ¥ = 106677,6 и квадрата коэффициента темперированной секунды музыкального ряда k = 1,0594... . Отметим, что две спектральные линии серии Лаймана с длиной волны l = 1215,67 и l ' = 1026,02 при умножении на коэффициенты: 4; 2,2449241; 1,7817974; 1,58740105 дают последовательно длины волн линий серий Бальмера, Пашена, Бреккета, Пфунда:
Сер. Сер. Сер. Сер. Сер.
Лаймана Бальмера Пашена Бреккета Пфунда
1,216·10-5х4=4,863·10-5х2,245=1,092·10-4х1,762=1,954·10-4х1,587 = 3,088·10-4.
1,026·10-5х4=4,104·10-5х2,245=9,213·10-5х1,762=1,642·10-4х1,587 = 2,508·10-4.
(В табл. 26 указаны стрелками.)
Процессы последовательного сквозного перехода величин спектральных линий из одной серии в другую при умножении на коэффициенты, являющиеся степенью одного и того же иррационального числа k = 1.0594... темперированной секунды музыкального ряда. Квадрат k2 = (1,0594,..)2 = 1,1224... похоже, определяет шаг поперечной волны, в узлах которой и располагаются электроны числа: 4 = (1,12246)12; 2,2449241 = (1Д2246)7; 1,7817974 = (1.12246)5; 1,58740105 = (1,12246)4,… и так далее ..., которые на сегодня не замечены в квантовой механике, случайностью быть не могут и отображают, по всей видимости, такую взаимосвязь между всеми ли ниями серий, при которой наличие любой линии в спектре свидетельствует о существовании смежных, через коэффициенты, линий и в других сериях. А, следовательно, серии спектральных линий водорода, занесенные в табл.26, по меньшей мере не полны. И если проводить деление всех уже известных линий названных серий, начиная с серии Пфунда, на соответствующие коэффициенты, то в столбце каждой последующей серии появятся новые спектральные линии, которые в настоящее время не отождествляются с водородом и будут обнаружены при анализе уже имеющихся спектрограмм. Но все же основное заключается в том, чтобы понять, линии каких элементов включают в себя серии от Бальмера до Пфунда и почему квантовая механика допускает возможность совмещения в одной серии линий спектров, относящихся к другим элементам или изотопам.
Подчеркну, что величина темперированной секунды есть одна двенадцатая степень от числа 2. И в своем степенном возрастании секунда проходит все числа натурального ряда таким образом, что величина образуемых ею чисел близка к числам натурального ряда. Следовательно, при знании радиуса любой из орбит атома, последнюю можно обозначить номером 1, что обусловливает нахождение радиусов некоторых других орбит, кратных степени коэффициента k и потому совпадающих с числами натурального ряда, а по ним и многих спектральных линий данного элемента. Именно включе ние в «постоянную» Ридберга теоретического радиуса боровской орбиты электрона, совпадающей с точно стью до четвертого знака с фактическим радиусом од ной из электронных орбит атома водорода и обуслови ло выявление части спектра водорода в виде спектральных серий, той части, которая соответствовала степени чисел натурального ряда и потому оказалась как бы подтверждением квантовой структуры расположения орбит в атоме. Для других элементов такое совпадение отсутствует, а потому и не удается теоретическое построение спектральных линий этих элементов.
Рассмотрим таблицу спектральных линий от Бальмера до Пфунда, полученную расчетом по формуле (6.16) с использованием коэффициента k = 1,12246... и коэффициента Ридберга, равного 109677,5 (табл. 26).
Таблица 26
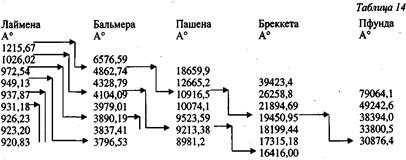
Таблица 27
| Серия | Серия | Серия | Сертия | Серия |
| Лаймана | Бальмера | Пашена | Бреккета | Пфунда |
| 3112,9 Ü | 12451Ü | 27953 Ü | 49807 Ü | 79064 |
| 2463,9 Ü | 9855,8 Ü | 22125 Ü | 39423 Ü | |
| 2077,9 Ü | 8311,6 Ü | 18659 Ü | ||
| 1938,8 Ü | 7755,2 Ü | 17409 Ü | 31020 Ü | 49242 |
| 1644,1 Ü | 6576,5 Ü | |||
| 1641,2 Ü | 6564,7 Ü | 14737 Ü | 26258 Ü | |
| 1511,6 Ü | 6046,6 Ü | 13547 Ü | 24186Ü | 38394 |
| 1410,41 Ü | 5641,6 Ü | 12665 Ü | ||
| 1368,4Ü | 5473,6 Ü | 12288 Ü | 21894 Ü | |
| 1330,8 Ü | 5323,2 Ü | 11950 Ü | 21293 Ü | 33800 |
| 1215,6 Ü | 4862,5 Ü | 10916 Ü | 19450 Ü | 30876 |
| 1137,4 Ü | 4549,8 Ü | 10214 Ü | 18189 Ü | |
| 1133,0 Ü | 4532,0 Ü | 10074 Ü | ||
| 1082,2 Ü | 4328,7 Ü | 9717,8 Ü | 17315 Ü | |
| 1060,5 Ü | 4242,2 Ü | 9523,5 Ü | ||
| 1026,0 Ü | 4104,0 Ü | 9213,3 Ü | 16416 Ü | 25081 |
| 1000,6 Ü | 4000,6 Ü | 8981,2 Ü | ||
| 994,75 Ü | 3979,0Ü | |||
| 972,52 Ü | 3890,1 Ü | |||
| 959,35 Ü | 3837,4 Ü | |||
| 949,13 Ü | 3796,5 Ü |
Покажу, опираясь на длины волн табл.26, какие спектральные линии, отсутствующие в современных справочниках, образуются посредством деления длин сериальных линий на коэффициенты: 4, 2,2449..., 1,7817..., 1,5874... и т.д. и могут быть обнаружены (табл. 27) при анализе спектров водорода. В сериях табл. 27 полужирным шрифтом обозначены длины линий всех известных серий, а простым, те из линий, которые в настоящее время не относятся к спектру водорода.
Вернемся к структуре атома и совокупности стоячих волн, определяющих взаимодействие ядра с электронами, входящими
в состав атома. Собственная пульсация ядра возбуждает в области его поверхности возникновение волн разрежения и сжатия эфира. Возникающая объемная волна имеет два определяющих параметра: продольную и поперечную длину волны. Продольная длина волны l пропорциональна расстоянию от центра ядра до его поверхности, т.е. радиусу атома а, и определяется произведением; l = 2p а.
Аналогично продольная длина n-й волны равна: l n = 2p аn. Особенность продольной волны в том, что она имеет неизменяемую по длине плотность и в момент возникновения отделяется от поверхности ядра, движется, удлиняясь к периферии атома. Практически в любом месте она представляет собой длину круга единой плотности, не имеющего поперечного направления. Вот это поперечное направление, определяемое удлинением радиуса ядра, и становится «истинной» длиной волны. Истинной потому, что именно в этом направлении происходит чередование сжатий и разрежений эфира, т.е. происходят те качественные изменения пространства, которые и образуют волну. (Название «истинное» дано для того, чтобы не было ассоциации с современным представлением поперечной волны.) 
Но двигаются они не одни. Навстречу им от других ядер в том же пространстве эфира двигаются истинные волны от окружающих ядер, имея ту же самую длину волны, амплитуду и фазу. (Если параметры волн не совпадут по количественной величине, то такие ядра перемещаются относительно друг друга до тех пор, пока не будет достигнуто совпадение этих параметров.) В результате сложения движущихся навстречу друг другу сжатий — разрежений эфира все межъядерное пространство «расчерчивается» стоячими волнами с чередующимися узлами и пучностями. То есть само пространство как бы квантуется стоячими волнами строго определенной поперечной длины, равной через узел длине двух несимметричных полуволн (l р - радиальная, рис. 82 ).
Отмечу, что движение поперечных волн происходит в пространстве изменяемой плот-ности эфира и потому гео-метрическая длина волны l р, находящейся ближе к поверх-ности ядра, будет меньше длины волны l р1 находящейся далеко от Рис. 82. ядра (эффект изменения плотности пространства), хотя физическая длина их останется неизменной.
На сегодняшний день способов определения длины истинной волны, похоже, не найдено. Однако можно полагать, что
длина эта пропорциональна темперированной секунде k = 1,05964... гармоничной русской матрицы, и квадрат этой секунды k 2 = 1,122462... есть та величина, на которую изменяется радиус ядра D R при пульса-ции, и это изменение становится длиной поперечной волны. (Однако полной уверенности в этом еще нет и не исключено, что именно коэффициент k , а не его квадрат определяет полную длину истинной волны. Тогда ее приведенный радиус равен: аn = l n /2p). А истинной волны вычисляется по формуле:
l = аnkn - а. (6.26)
Найдем величину l n, начиная, например, от боровской орбиты.
Длина полуволны от боровской орбиты во вне равна:
абk = 5,292·10-9·1,059463... = 5,6067·10-9 см,
l 2 /2 = ао - абk = 3,1468·10-10 см.
Аналогично можно рассчитать длину истинной волны в любой области атома. Она разделяется узлом на две части. Узел это та область пространства атома, которую может занимать, а может не занимать («пус той» узел) один из электронов атома (возможно, несколько?). Таким образом, узлы волн «квантуют» пространство электрона пропорционально k, «созда вая» зону орбитального «обитания» электронов. Возможность перемещения электронов на другие орбиты ограничена их собственными свойствами, в первую очередь энергией, частотой самопульсации, и пучностями, отделяющими один узел от другого. Эта возможность, похоже, реализуется только в двух случаях, когда изменение свойств электрона медленно передвигает его через зону пучности в зону другого узла и он, передвигаясь, совершает «малый» скачок без испускания кванта, и когда плотность тела электрона превышает порог перехода узла (т.е. плотностный порог от a к a '), и происходит испускание фотона «большим» скачком (переход с орбиты на орбиту).
В этом случае электроны, достигнув порога a ' (порога четырехмерной плотности), испускают четырехплотностный фотон, и, оставляя тем самым свою «разрыхленную» трехмерную плотность a , перемещаются (точнее «загоняются» напряженностью ядра) на более близкую к ядру орбиту, на ту, где полностью «восстанавливается» их трехмерностность пропорционально коэффициенту Ридберга. Вернемся к нему (6.19) и рассмотрим составляющую его структуру:
R ¥ = 1/4p a аб = 1/2a l . (6,27)
Из (6.27) ясно, что испускание фотона есть следствие достижения электроном данной орбиты предельной плотности трехмерного состояния 2a (Возможно образование внутри электрона трехмерной плотности некоего керна плотности четырехмерной.) «Сосуществование» двух тел различной плотности нарушается, и тело четырехмерной плотности (керн), покидая электрон, улетает в виде фотона за пределы атома, а «облегченный» по плотности электрон перемещается на ту орбиту, которая пропорциональна его вновь «набранной» плотности и установившейся длине волны. В этом процессе важно то, что фотон вылетает до начала перемещения электрона на новую орбиту. Именно это обстоятельство сужает ширину спектральной линии фотона.
Дата добавления: 2018-11-24; просмотров: 285; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!