Сходимость собственных векторов
Будем предполагать, что 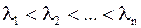 и
и 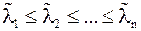 (этого всегда можно добиться, переставив столбцы матриц
(этого всегда можно добиться, переставив столбцы матриц 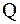 и
и 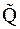 ).
).
| Лемма 7. | Если 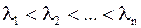 , , 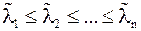 , ,  , ,
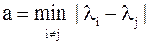 ,
то ,
то 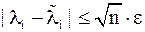 , , 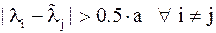 . .
|
| Док–во | оставляется в качестве упражнения. |
Т.к. собственные векторы 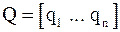 матрицы
матрицы 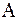 определяются с точностью до их направления, будем считать, что
определяются с точностью до их направления, будем считать, что 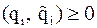 (
(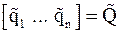 – приближения к собственным векторам матрицы
– приближения к собственным векторам матрицы 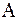 ), т.е. диагональные элементы матрицы
), т.е. диагональные элементы матрицы  неотрицательны.
неотрицательны.
| Теорема 3 | (оценка приближения собственных векторов). |
В условиях леммы 7 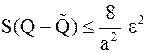 . .
| |
| Док–во. | Т.к. 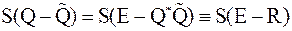 и из доказательства теоремы 2 ( и из доказательства теоремы 2 (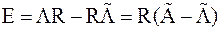 ) и леммы 7 следует, что ) и леммы 7 следует, что 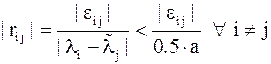 , то , то 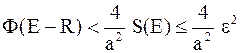 .
Осталось оценить .
Осталось оценить 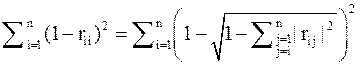 (здесь мы воспользовались условием (здесь мы воспользовались условием  ).
Т.к. ).
Т.к.  , то , то
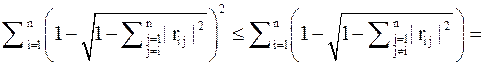
 .
Подводя итог, имеем .
Подводя итог, имеем
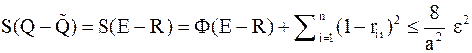 . .
|
Литература
1. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. - М.: Л.: Физматгиз, 1963.
2. Коновалов А.Н. Введение в вычислительные методы линейной алгебры.- Новосибирск: ВО "Наука", Сибирская издательская фирма, 1993.
3. Воеводин В.В. Вычислительнные основы линейной алгебры. - М.: Наука, 1977.
4. Годунов С.К. Решение систем линейных уравнений. - Новосибирск: Наука, Сиб. отд-ние, 1980.
5. Бахвалов Н.С. Численные методы. - М.: Наука, 1975.
6. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989.
[1] Конспект подготовлен при финансовой поддержке проекта № 274 ФЦП "Интеграция".
Дата добавления: 2015-12-17; просмотров: 21; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
