Метод сопряженных градиентов
Пусть матрица системы 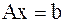 симметрична и положительно определена. Построим (
симметрична и положительно определена. Построим ( )
) 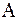 –ортогональный базис
–ортогональный базис  в
в 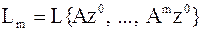 .
.
1. 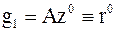 – базис в
– базис в 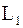
| 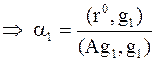 , , 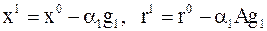 . .
|
Заметим, что 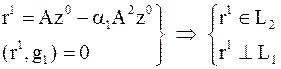
| |
Предположим, что выполнили 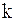 шагов: шагов: 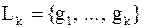 и и 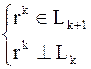 .
Определим .
Определим 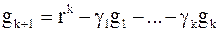 : : 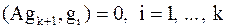 ,
т.е. ,
т.е.  , т.к. , т.к. 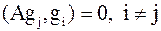 .
Заметим, что .
Заметим, что 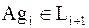 и и 
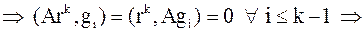
| |
 –шаг. –шаг.
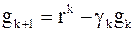

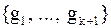 – базис в
– базис в 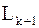
| 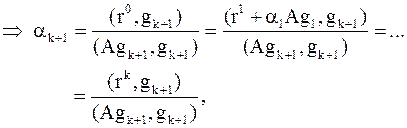
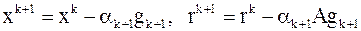 . .
|
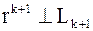 ,
т.к. ,
т.к. 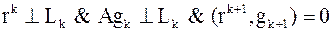 .
Т.к. .
Т.к.  и
и 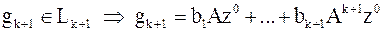 , то , то
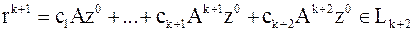
 предположения мат. индукции выполнены,
мы построили метод сопряженных градиентов. предположения мат. индукции выполнены,
мы построили метод сопряженных градиентов.
|
Теорема.
Если 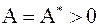 , то метод сопряженных градиентов продолжается до получения решения системы
, то метод сопряженных градиентов продолжается до получения решения системы 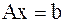 за
за 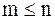 итераций (пока
итераций (пока 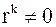 ) и
) и
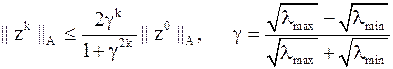 .
.
Доказать теорему в качестве упражнения.
Дата добавления: 2015-12-17; просмотров: 18; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
