Полином Чебышева и решение задачи оптимизации параметров
Очевидно, что 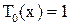 ,
, 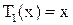 – полиномы.
– полиномы.
Т.к. 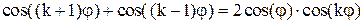 , то при
, то при  имеем
имеем 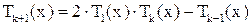 – полином при любом
– полином при любом 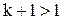 .
.
Точки экстремумов 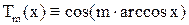 :
: 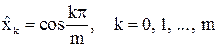 :
:
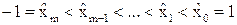 ,
, 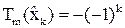 .
.
Корни полинома 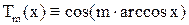 :
:  :
:
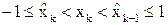 ,
, 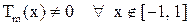 .
.
Линейное преобразование 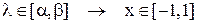 :
: 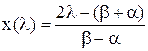 .
.
Рассмотрим полином:  .
.
Очевидно, что 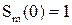 ,
, 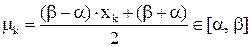 – корни полинома.
– корни полинома.
Покажем, что этот полином наименее уклоняется от нуля на интервале  среди всех полиномов
среди всех полиномов 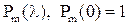 , т.е.
, т.е. 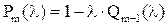 .
.
| Теорема. | Если  , то , то  . .
|
| Док-во. | Пусть 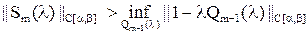 ,
тогда ,
тогда 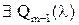 : : 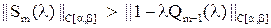 .
Так как
· полином .
Так как
· полином 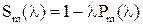 имеет экстремумы (одинаковые по модулю) в точках имеет экстремумы (одинаковые по модулю) в точках  : : 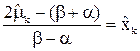 , , 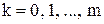 : :  , и , и 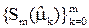 знакопеременна:
то разность знакопеременна:
то разность 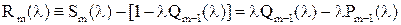 · полином степени
· полином степени 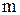 ,
· последовательность ,
· последовательность  знакопеременна знакопеременна 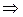 в интервале в интервале  имеется имеется 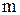 попарно различных корней полинома попарно различных корней полинома 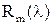 (т.к. внутри интервала (т.к. внутри интервала 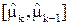 имеется хотя бы один корень),
· имеется хотя бы один корень),
· 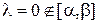 – корень ( – корень (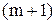 –ый) полинома –ый) полинома 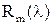 (именно здесь мы использовали условие (именно здесь мы использовали условие  ). ).
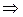 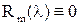 , т.е. , т.е. 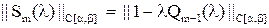 – противоречие.
Следовательно, – противоречие.
Следовательно, 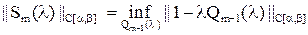 . .
|
Осталось вычислить 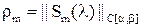 .
.
| Теорема. | Если  , то , то 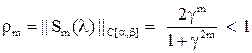 , где , где 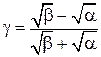 . .
|
| Док-во. | Очевидно, 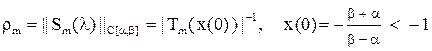 .
Для вычисления .
Для вычисления  воспользуемся формулой воспользуемся формулой
 при при 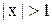 . .
|
Заметим, что
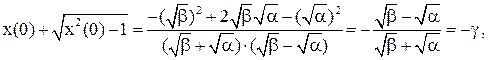
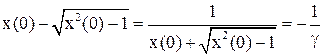 .
Тогда .
Тогда 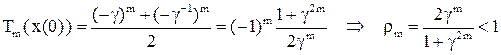 .
Док-во формулы .
Док-во формулы 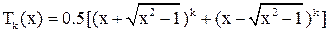 при при 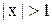 .
Действительно, .
Действительно, 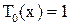 и и 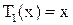 .
Осталось проверить, что .
Осталось проверить, что 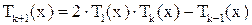 или или
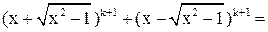
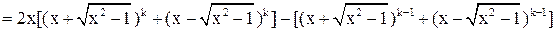 .
Пусть .
Пусть 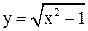 , тогда , тогда


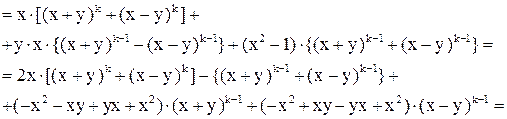
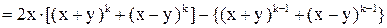 , что и тр. док. , что и тр. док.
|
Итак,  – решение задачи оптимизации параметров за
– решение задачи оптимизации параметров за 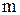 шагов.
шагов.
Дата добавления: 2015-12-17; просмотров: 19; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
