Задача оптимизации параметров
Параметры 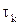 в итерационном методе
в итерационном методе 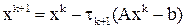 можно выбирать из условия минимизации спектрального радиуса
можно выбирать из условия минимизации спектрального радиуса 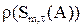 матрицы (оператора) ошибки за
матрицы (оператора) ошибки за 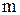 шагов:
шагов: 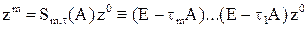 .
.
Если все параметры взять одинаковыми, то мы получим метод простой итерации и он сходится при известных условиях, т.е. предлагаемый способ построения итерационного метода может привести только к лучшему методу.
Мы будем предполагать, что 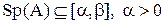 , т.е. все собственные значения матрицы системы линейных уравнений
, т.е. все собственные значения матрицы системы линейных уравнений 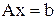 положительны.
положительны.
Т.к. 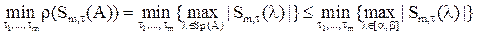 , а последнюю минимаксную задачу решать проще (почему?), мы будем искать
, а последнюю минимаксную задачу решать проще (почему?), мы будем искать 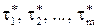 :
:
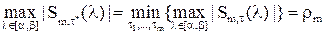 ,
,
т.е. решать задачу о поиске полинома 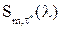 степени
степени 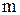 , наименее уклоняющегося от нуля на отрезке
, наименее уклоняющегося от нуля на отрезке  при условии
при условии 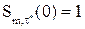 .
.
Тогда, т.к. 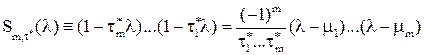 , где
, где 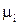 – корни полинома
– корни полинома 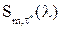 ,
, 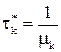 и
и 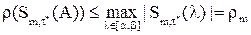 .
.
Если 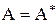 , то
, то 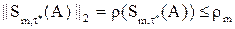 и, следовательно,
и, следовательно,
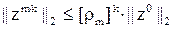
– оценка сходимости метода.
Дата добавления: 2015-12-17; просмотров: 19; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
