Корректность задачи на собственные значения
Известно, что все собственные значения матрицы 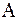 являются корнями характеристического полинома
являются корнями характеристического полинома
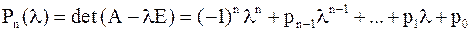 ,
,
а коэффициенты 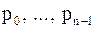 – непрерывные функции элементов матрицы
– непрерывные функции элементов матрицы 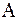 .
.
Пусть 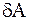 – матрица с “малыми” по величине элементами,
– матрица с “малыми” по величине элементами, 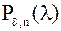 – характеристический полином матрицы
– характеристический полином матрицы 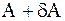 . Следствием непрерывности
. Следствием непрерывности 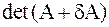 как функции элементов матрицы
как функции элементов матрицы 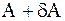 является
является
Лемма 1. 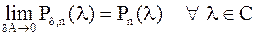 .
.
| Лемма 2. | В любом круге на комплексной плоскости с центром в точке 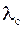 и радиуса и радиуса 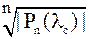 лежит хотя бы один корень полинома лежит хотя бы один корень полинома 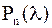 . .
|
| Док–во. | Разложим 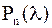 в ряд Тейлора в точке в ряд Тейлора в точке 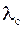 : :
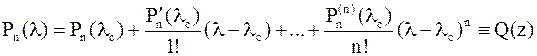 , где , где  .
Пусть .
Пусть 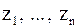 – корни полинома – корни полинома 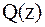 , среди которых корень с минимальной абсолютной величиной имеет номер , среди которых корень с минимальной абсолютной величиной имеет номер  .
Так как .
Так как 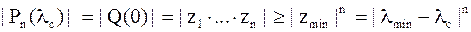 , то , то 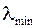 (корень полинома (корень полинома 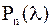 ) лежит в круге радиуса ) лежит в круге радиуса 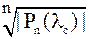 . .
|
| Лемма 3. | Если 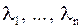 – корни полинома – корни полинома 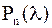 , то , то 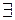 нумерация корней нумерация корней 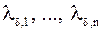 полинома полинома 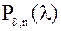 : : 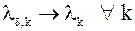 при при  . .
|
| Док–во | методом матиндукции по степени полинома.
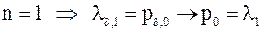 .
Пусть лемма верна при .
Пусть лемма верна при 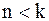 . .
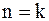 : из леммы 2 : из леммы 2  .
Т.к. .
Т.к. 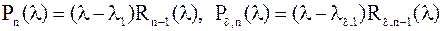 и
и 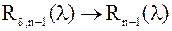 , то , то 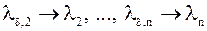 . .
|
Степенной метод вычисления максимального собственного значения матрицы 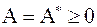
Идея метода: для заданного вектора 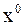 рассмотрим его
рассмотрим его 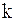 –ю итерацию
–ю итерацию 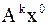 ,
,
если 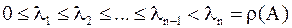 – собственные значения,
– собственные значения,
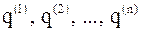 – соответствующие им собственные векторы, то
– соответствующие им собственные векторы, то
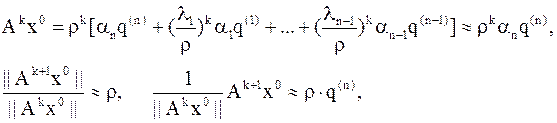
где 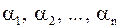 – коэффициенты (неизвестные!)
– коэффициенты (неизвестные!)
разложения вектора 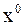 по базису
по базису 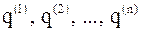 .
.
Итерационный процесс

называется степенным методом вычисления максимального собственного значения матрицы 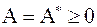 :
:
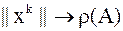 ,
, 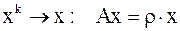 ,
,
если проекция начального вектора 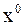 на линейную оболочку собственных векторов, соответствующих
на линейную оболочку собственных векторов, соответствующих 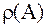 , не равна 0.
, не равна 0.
Док–во. Пусть 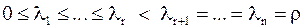 – собственные значения,
– собственные значения,
|
|
|
 – собственные векторы матрицы
– собственные векторы матрицы 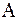 , и
, и

Тогда 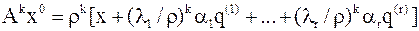 и,
и,
т.к. 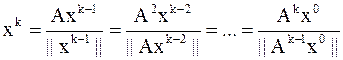 ,
,  ,
,
то 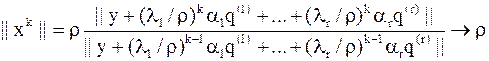 ,
,
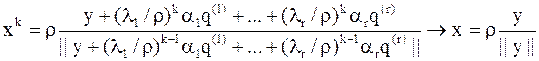 .
.
Замечание. Сходимость степенного метода не зависит от выбора в нем векторной нормы, т.к. все нормы в  эквивалентны.
эквивалентны.
Степенной метод вычисления минимального собственного значения матрицы 
Задача вычисления минимального собственного значения матрицы 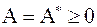 легко сводится к задаче вычисления максимального собственного значения матрицы
легко сводится к задаче вычисления максимального собственного значения матрицы 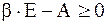 , где
, где 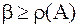 , так как
, так как 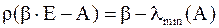 .
.
Оценку для 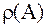 легко найти:
легко найти: 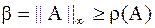 . Тогда
. Тогда
итерационный процесс
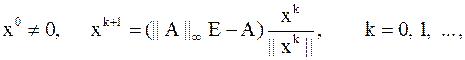
называется степенным методом вычисления минимального собственного значения матрицы 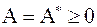 :
: 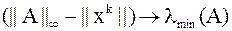 ,
,
если проекция начального вектора 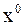 на линейную оболочку собственных векторов, соответствующих
на линейную оболочку собственных векторов, соответствующих 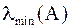 , не равна 0.
, не равна 0.
Справедливость этого утверждения является следствием сходимости степенного метода вычисления спектрального радиуса матрицы 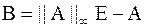 .
.
Дата добавления: 2015-12-17; просмотров: 21; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
