Приведение самосопряженной матрицы к трехдиагональному виду ортогональным преобразованием подобия с помощью матриц вращения
Как и раньше, через 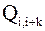 будем обозначать элементарную матрицу вращения, отличающуюся от единичной матрицы
будем обозначать элементарную матрицу вращения, отличающуюся от единичной матрицы
двумя диагональными элементами:  , и двумя внедиагональными элементами:
, и двумя внедиагональными элементами: 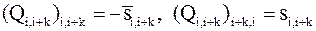 ,
, 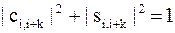 .
.
Выполним и
| 1–й шаг. | Исключение элементов 1–го столбца матрицы 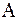 , начиная с 3–его, с помощью последовательного умножения на унитарные матрицы , начиная с 3–его, с помощью последовательного умножения на унитарные матрицы  : : 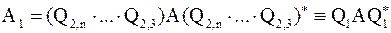 . .
|
| 2–й шаг. | Исключение элементов 2–го столбца матрицы 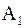 , начиная с 4–ого, с помощью последовательного умножения на унитарные матрицы , начиная с 4–ого, с помощью последовательного умножения на унитарные матрицы 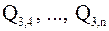 : : 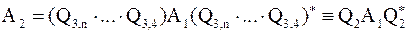 . .
|
| … | ………………….. |
| k–й шаг. | Исключение элементов k–го столбца матрицы 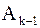 , начиная с (k+2)–ого, с помощью последовательного умножения на матрицы , начиная с (k+2)–ого, с помощью последовательного умножения на матрицы 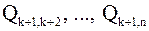 : : 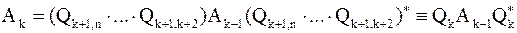 . .
|
| … | ………………….. |
| (n–2)–й шаг. | Исключение последнего элемента (n-2)–го столбца матрицы 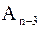 с помощью умножения на матрицу с помощью умножения на матрицу 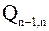 : :
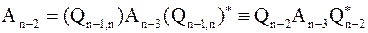 . .
|
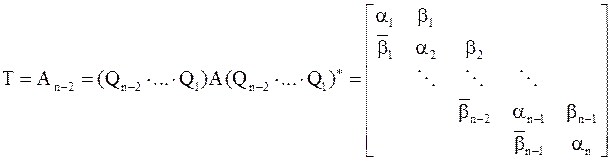 ,
,
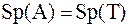 .
.
Если 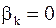 , то
, то 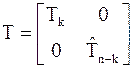
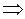
 ,
,
т.е. поиск собственных значений самосопряженной матрицы сводится к задаче на собственные значения якобиевых трехдиагональных матриц.
| Лемма 2. | Самосопряженная матрица подобна трехдиагональной вещественной матрице. |
| Док–во. | Только что мы привели самосопряженную матрицу  к трехдиагональному виду ортогональным преобразованием подобия: к трехдиагональному виду ортогональным преобразованием подобия: 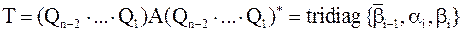 .
Определим матрицу .
Определим матрицу  : (предполагая : (предполагая 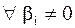 ) )
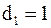 , , 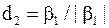 ,..., ,..., 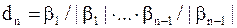 .
Тогда .
Тогда 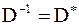 , ,  . .
|
Якобиевы матрицы
Вещественная матрица
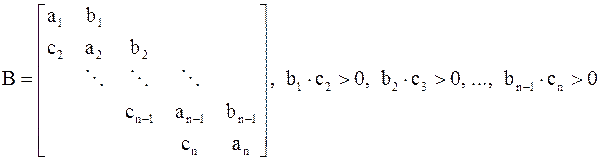 ,
,
называется якобиевой (у нас 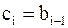 ).
).
| Лемма 3. | Пусть 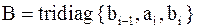 – якобиева матрица, тогда
1. – якобиева матрица, тогда
1.  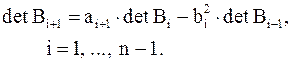 2. если
2. если  , то , то 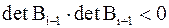 , если , если 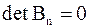 , то , то 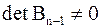 . .
|
| Док–во | оставляется читателю в качестве упражнения. |
| Лемма 4. | Собственные значения якобиевой матрицы 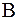 попарно различные (простые). попарно различные (простые).
|
| Док–во. | Т.к. размерность ядра симметричной матрицы 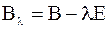 совпадает с кратностью совпадает с кратностью 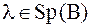 , а из леммы 3 следует, что у вырожденной якобиевой матрицы , а из леммы 3 следует, что у вырожденной якобиевой матрицы 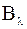 минор минор 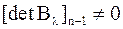 , то , то 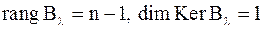 и и 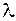 простое собственное значение матрицы простое собственное значение матрицы 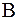 . .
|
|
|
|
| Теорема. | Пусть 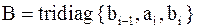 – якобиева матрица, тогда – якобиева матрица, тогда
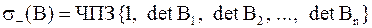 ,
если ,
если 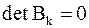 приписать знак приписать знак 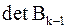 . .
|
| Док–во. | 1. Если 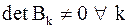 , то это лемма 1. , то это лемма 1.
|
2. Пусть 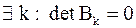 . Пусть
. Пусть  .
.
Определим 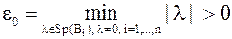 и рассмотрим якобиевы матрицы
и рассмотрим якобиевы матрицы  .
.
Т.к. 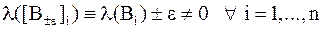 , то
, то
а) 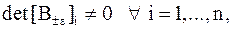 (т.к. определитель матрицы равен произведению ее собственных значений),
(т.к. определитель матрицы равен произведению ее собственных значений),
б) 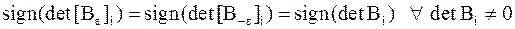 ,
,
в) 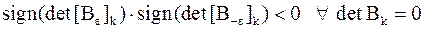 ,
,
(т.к. из леммы 4 следует, что 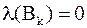 простое и отрицательных собственных значений у матрицы
простое и отрицательных собственных значений у матрицы 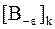 на одно больше, чем у матрицы
на одно больше, чем у матрицы 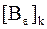 ),
),
г) 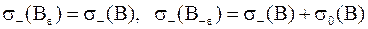 .
.
Из леммы 1, а) и г) следует, что
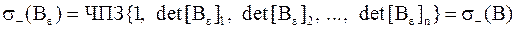 ,
,
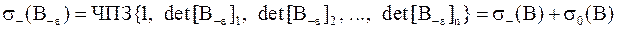 ,
,
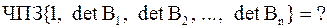
Подсчитаем эти числа:
Из б) следует, что если 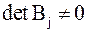 и
и  , то перемена знака происходит (или нет) одновременно в этих последовательностях.
, то перемена знака происходит (или нет) одновременно в этих последовательностях.
Случай  .
.
Из леммы 3 имеем 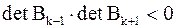 , отсюда и из б) следует
, отсюда и из б) следует  и на участках
и на участках
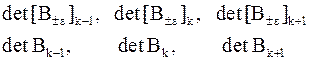
по одной перемене знака.
Случай 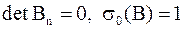 . Отсюда, из в) и г) следует, что
. Отсюда, из в) и г) следует, что
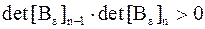 ,
, 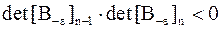 ,
,
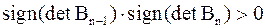 .
.
Следовательно, (если 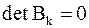 приписать знак
приписать знак 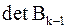 ) последовательности миноров матриц
) последовательности миноров матриц  и
и 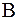 имеют одинаковые знаки. Теорема доказана.
имеют одинаковые знаки. Теорема доказана.
О вычислении ЧПЗ
Для вычисления 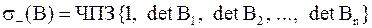 якобиевой матрицы
якобиевой матрицы 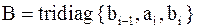 достаточно знать знак каждого
достаточно знать знак каждого 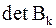 . Если
. Если
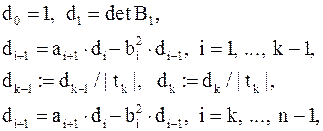
(обычно выбирают 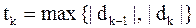 ), то
), то 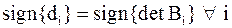 и
и 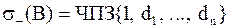 . Нормировку можно применять неоднократно, что позволит избежать быстрого роста (переполнения) чисел
. Нормировку можно применять неоднократно, что позволит избежать быстрого роста (переполнения) чисел 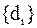 .
.
Дата добавления: 2015-12-17; просмотров: 32; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
