О вычислении собственного вектора
| Лемма 5. | Последняя компонента собственного вектора 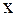 якобиевой матрицы якобиевой матрицы 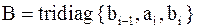 не равна нулю. не равна нулю.
|
| Док–во. | Пусть 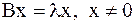 . Предположим, что . Предположим, что 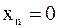 . Тогда . Тогда
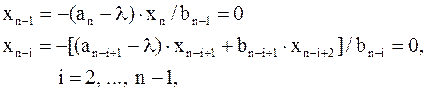
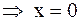 – противоречие, значит – противоречие, значит 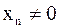 . .
|
Собственный вектор 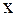 якобиевой матрицы
якобиевой матрицы 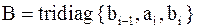 мы можем, положив
мы можем, положив 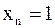 , вычислить по формулам
, вычислить по формулам
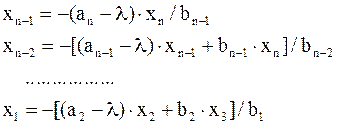
или решив систему
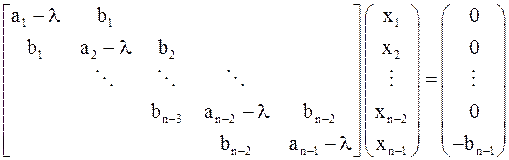
с неособенной матрицей.
Лекция 13. Метод вращений (Якоби)
Для самосопряженной матрицы 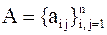 существует унитарная матрица
существует унитарная матрица 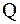 (столбцы которой – собственные векторы матрицы
(столбцы которой – собственные векторы матрицы 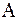 ):
):
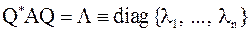
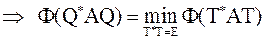 , где
, где 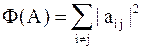 .
.
Идея:
построить 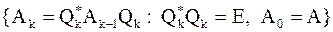 :
: 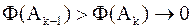 , тогда на диагональные элементы
, тогда на диагональные элементы 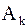 будут приближать собственные значения, а столбцы
будут приближать собственные значения, а столбцы 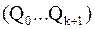 – собственные векторы матрицы
– собственные векторы матрицы 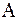 .
.
Определим 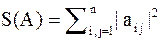 .
.
| Лемма 1. | Для любых квадратной матрицы 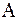 и унитарной матрицы и унитарной матрицы 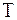 имеем имеем
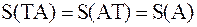 . .
|
| Док–во. | Если 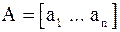 , то , то
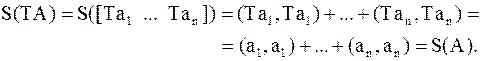
|
В качестве матриц  будем выбирать элементарные матрицы вращения.
будем выбирать элементарные матрицы вращения.
| Лемма 2. | Пусть 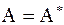 , , 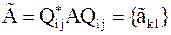 ,
где ,
где 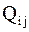 – элементарная матрица вращения, тогда – элементарная матрица вращения, тогда
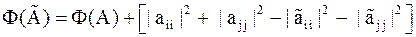 . .
|
| Док–во. | Заметим, что изменились только строки и столбцы с номерами 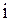 , , 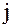 .
Тогда, используя лемму 1, получим .
Тогда, используя лемму 1, получим
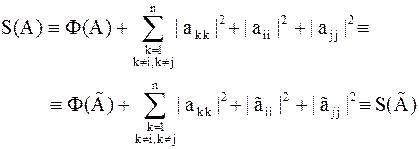 откуда следует утверждение леммы.
откуда следует утверждение леммы.
|
Выбор вращения
Для простоты будем полагать, что матрица 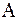 вещественная. Выразим разность
вещественная. Выразим разность 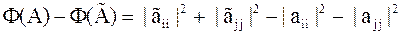 через элементы матрицы
через элементы матрицы 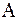 .
.
| Лемма 3. | Пусть 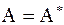 , , 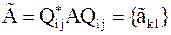 , где , где 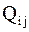 – элементарная матрица вращения ( – элементарная матрица вращения (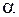 – угол вращения), тогда – угол вращения), тогда
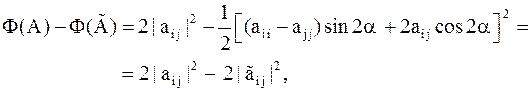
|
| Док–во. | Требуемые равенства выводятся из соотношения
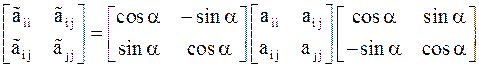 . .
|
| Лемма 4. | Пусть 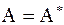 , , 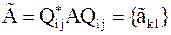 ,
где ,
где 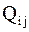 – элементарная матрица вращения такая, что – элементарная матрица вращения такая, что
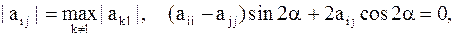 то
то 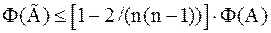 . .
|
| Док–во. | Требуемое неравенство следует из
равенства 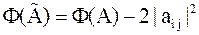 и оценки и оценки 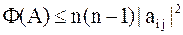 . .
|
Следующая лемма обеспечивает существование для леммы 4 матрицы 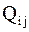 .
.
|
|
|
| Лемма 5. | Решением уравнения 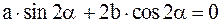 при при 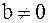 является угол является угол 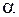 такой, что такой, что
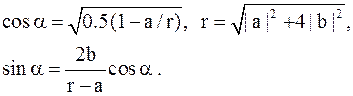
|
| Док–во | осуществляется непосредственной проверкой. |
Из последних двух лемм следует справедливость теоремы сходимости метода.
| Теорема 1. | Последовательность матриц 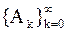 метода вращений: метода вращений:
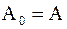 , , 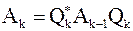 , где , где 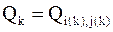 – матрица вращения, определяемая по формулам лемм 4 и 5,
для решения полной проблемы на собственные значения – матрица вращения, определяемая по формулам лемм 4 и 5,
для решения полной проблемы на собственные значения 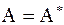 , сходится к диагональному виду, т.е. , сходится к диагональному виду, т.е. 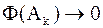 , причем , причем
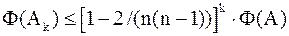 . .
|
Из теоремы 1 
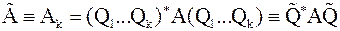 ,
, 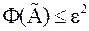 .
.
Пусть 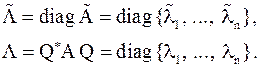
Дата добавления: 2015-12-17; просмотров: 23; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
