Применение ортогонализации и степенного метода для вычисления очередного собственного значения
Предположим, что собственное значение 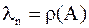 и соответствующий ему собственный вектор (какой–то!)
и соответствующий ему собственный вектор (какой–то!) 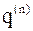 матрицы
матрицы 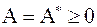 мы приближенно (например степенным методом) вычислили:
мы приближенно (например степенным методом) вычислили: 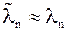 ,
, 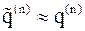 .
.
Построим симметричную положительно определенную матрицу 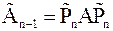 , где матрица
, где матрица  – ортогональный проектор на подпространство
– ортогональный проектор на подпространство  , ортогональное вектору
, ортогональное вектору 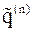 .
.
Докажите, что спектр матрицы 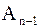 (т.е.
(т.е. 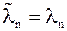 ,
, 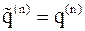 ) состоит из собственных значений
) состоит из собственных значений 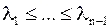 матрицы
матрицы 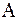 и нуля (вектор
и нуля (вектор 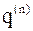 принадлежит ее ядру).
принадлежит ее ядру).
Отсюда следует, что, если  (а степенной метод такую сходимость гарантирует), то
(а степенной метод такую сходимость гарантирует), то 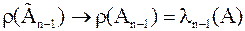 .
.
Следовательно, применяя степенной метод для матрицы 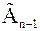 , мы получим приближение к
, мы получим приближение к 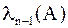 и
и 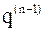 – очередным собственным значению и вектору матрицы
– очередным собственным значению и вектору матрицы 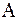 .
.
Эту процедуру можно продолжать до тех пор, пока мы не получим все собственные значения.
Лекция 12. Метод деления пополам (бисекций)
Для самосопряженной матрицы 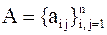 имеет место закон инерции:
имеет место закон инерции:
если матрицу 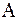 конгруэнтным преобразованием привести к диагональному виду:
конгруэнтным преобразованием привести к диагональному виду: 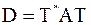 , где
, где 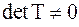 , то от матрицы
, то от матрицы 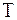 (способа преобразования) не зависит
(способа преобразования) не зависит
· 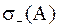 – количество отрицательных элементов,
– количество отрицательных элементов,
· 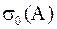 – количество нулевых элементов,
– количество нулевых элементов,
· 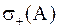 – количество положительных элементов на диагонали
– количество положительных элементов на диагонали 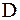 .
.
Нам известно (из теоремы и алгоритма 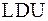 –разложения), что если все
–разложения), что если все 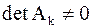 , то
, то 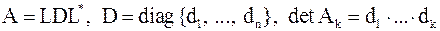 .
.
Следовательно, в этом случае за конечное число действий мы можем определить 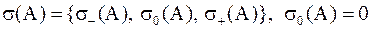 .
.
Матрица 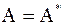 преобразованием подобия ортогональной матрицей
преобразованием подобия ортогональной матрицей 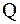 (конгруэнтным преобразованием) из собственных векторов приводится к диагональному виду
(конгруэнтным преобразованием) из собственных векторов приводится к диагональному виду 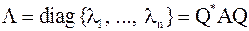 . Следовательно,
. Следовательно,
|
|
|
· 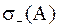 = количеству отрицательных,
= количеству отрицательных,
· 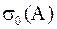 = количеству нулевых,
= количеству нулевых,
· 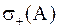 = количеству положительных собственных значений матрицы
= количеству положительных собственных значений матрицы 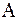 ,
,
и, используя 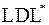 –разложение, мы можем эти числа определить.
–разложение, мы можем эти числа определить.
Подытожим эти рассуждения в виде следующей леммы.
| Лемма 1. | Если матрица 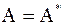 и и 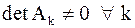 ,
то количество ее отрицательных собственных значений ,
то количество ее отрицательных собственных значений
 – число перемен знака.
– число перемен знака.
|
| Док–во | леммы оставляется в виде упражнения. |
Идея метода бисекций вычисления 
 , т.к.
, т.к. 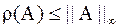 , т.е. все собственные значения
, т.е. все собственные значения 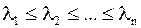 матрицы
матрицы 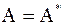 лежат в этом интервале.
лежат в этом интервале.
Определим в какой половине интервала  лежит
лежит 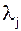 . Для этого вычислим
. Для этого вычислим  – количество собственных значений меньших
– количество собственных значений меньших 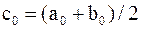 . Если
. Если 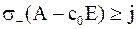 , то
, то 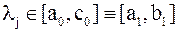 , иначе
, иначе 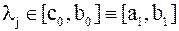 .
.
Через 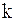 таких шагов получим:
таких шагов получим: 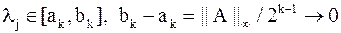 , т.е. мы можем получить оценку искомого собственного числа с любой точностью.
, т.е. мы можем получить оценку искомого собственного числа с любой точностью.
Дата добавления: 2015-12-17; просмотров: 22; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
