Фрагмент решения задачи в Mathcad .

Одноканальная СМО с ожиданием
Рассмотрим функционирование одноканальной системы S, в которую поступает простейший поток требований интенсивностью λ. Интенсивность потока обслуживания равна μ.
По числу заявок, находящихся в системе, обозначим состояния системы: S 0 , S 1 , S 2 ,…, Sk ,… Sn , где Sk – состояние системы, когда в ней находится k заявок (одна обслуживается, остальные k -1 стоят в очереди). Никаких ограничений на длину очереди нет. Примерами таких систем может служить телефон-автомат, кассир в магазине, железнодорожная касса и т.д. Так как поток заявок и обслуживания ординарен, и число состояний системы бесконечно, граф состояний такой системы изображается в виде схемы гибели и размножения на рисунке 4:
 |
Рисунок 4- Одноканальная СМО с ожиданием.
Интенсивность μ, потока обслуживаний не меняется при переходе из состояния Sk в состояние Sk -1 и обратна по величине среднему времени обслуживания заявки:
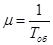 (22)
(22)
Финальные вероятности состояний такой системы существуют только в случае, если выполнено условие ρ < 1 , так как в этом случае очередь не будет расти до бесконечности.
Уравнение для нахождения р0 получим аналогично тому как это было сделано для одноканальной системы с отказами:
 (23)
(23)
|
|
|
С учетом формулы:
 , (24)
, (24)
получим
 (25)
(25)
где ρ – показатель нагрузки канала обслуживания.
Так как при ρ < 1 предельные вероятности существуют, то выражении ев скобках представляет собой сумму бесконечного числа членов убывающей геометрической прогрессии, предел которого равен:
 (26)
(26)
откуда
 (27)
(27)
Формула для вероятностей предельных состояний будут иметь вид:
 ,
,  , ……. ,
, ……. ,  ,
,  … (28)
… (28)
Предельные вероятности состояний Sk также образуют убывающую геометрическую прогрессию, поэтому наиболее высокой будет вероятность р0, то есть вероятность простоя системы и готовности принять заявку к обслуживанию.
Формулы для расчета основных показателей эффективности работы системы.
Вероятность отказа в обслуживании заявки при условии неограниченности очереди равна нулю, так как все заявки, в итоге будут обслужены. Отсюда вероятность обслуживания (а также и относительная пропускная способность системы) равна единице:
|
|
|
 . (29)
. (29)
Абсолютная пропускная способность равна интенсивности входящего потока, так как обслуживаются все заявки:
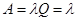 (30)
(30)
Среднее время обслуживания каналом одной заявки:
 (31)
(31)
Так как вероятность того, что в системе находится k заявок, равна р k , среднее число заявок в системе определим как математическое ожидание числа заявок в системе (под обслуживанием и в очереди ):
 (32)
(32)
Подставив в формулу выражение для рk , получим:
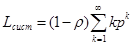 (33)
(33)
При ρ < 1 такой ряд сходится, что можно проверить, воспользовавшись каким-либо признаком сходимости числовых рядов.
Заметим, что kρk - это производная по ρ функции ρk .
Применив правило вычисления производной суммы, поменяем местами знак суммы и знаки дифференцирования:
|
|
|
 (34)
(34)
Но теперь под знаком суммы находится убывающая геометрическая прогрессия со знаменателем, меньшим единицы. Поэтому
 (35)
(35)
Среднее число заявок под обслуживанием L об найдем как математическое ожидание числа обслуживаемых заявок. Это либо 0 заявок, когда канал свободен, либо 1 заявка, когда канал занят:
 (36)
(36)
Отсюда видно, что среднее число заявок под обслуживанием равно вероятности того, что канал занят:
 (37)
(37)
Очевидно, среднее число заявок в очереди равно разности между числом заявок в системе и числом обслуживаемых заявок:
 (38)
(38)
Среднее время пребывания заявки в системе (или в очереди) можно найти по формулам Литтла, разделив среднее число заявок в системе (в очереди) на интенсивность потока заявок:
 (39)
(39)
 (40)
(40)
|
|
|
Формулы Литтла основаны на том, что если система справляется с потоком заявок, то интенсивности входящего и выходящего потока заявок равны, то есть обслуживаются все заявки, поступающие в систему.
Одноканальную СМО с ожиданием можно рассмотреть в Mathcad.
Дата добавления: 2018-10-26; просмотров: 477; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
