Микро- и макросостояния. Статистический вес. Обратимые и необратимые процессы. Энтропия. Закон возрастания энтропии. Теорема Нернста.
+ Билет 30.
Статистический вес - это число способов, которыми может быть реализовано данное состояние системы. Статистические веса всех возможных состояний системы определяют её энтропию.
Обратимые и необратимые процессы.
Обратимый процесс (то есть равновесный) — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.
(Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.
Обратимые процессы дают наибольшую работу.
На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.)
Необратимый процесс - процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы.
В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс.
Записанное утверждение является ещё одной формулировкой второго начала термодинамики.
Теорема Нернста (Третье начало термодинамики) — физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных.
Третье начало термодинамики может быть сформулировано так:
«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».
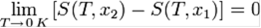
или
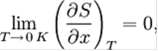
Где x — любой термодинамический параметр.
(Третье начало термодинамики относится только к равновесным состояниям.
Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение):
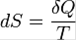 ,
,
третье начало термодинамики может быть использовано для точного определенияэнтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.
Согласно третьему началу термодинамики, при  значение
значение  .)
.)
Билет 32.
Дата добавления: 2018-10-26; просмотров: 387; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
