Свободные затухающие колебания. Дифференциальное уравнение и его решение. Декремент, логарифмический декремент, коэффицент затухания. Время релаксации.
Свободные затухающие колебания
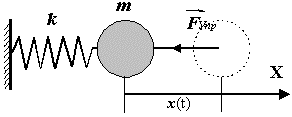
Если можно пренебречь силами сопротивления движению и трением, то при выведении системы из положения равновесия на груз будет действовать только сила упругости пружины.
Запишем уравнение движения груза, составленное по 2-му закону Ньютона:
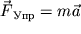
Спроектируем уравнение движения на ось X.
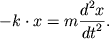
преобразуем: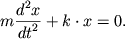 
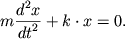т.к.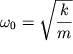 
это дифференциальное уравнение свободных гармонических незатухающих колебаний.
Решение уравнения имеет вид:
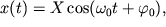
Дифференциальное уравнение и его решение:
Во всякой колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать.
Сила сопротивления пропорциональна величине скорости:
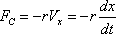
r – постоянная величина, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила и скорость имеют противоположные направления.
Уравнение второго закона Ньютона при наличии сил сопротивления имеет вид:
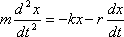
Применив обозначения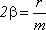 
, 
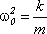, перепишем уравнение движения следующим образом:
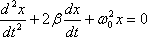
Это уравнение описывает затухающие колебания системы
Решение уравнения имеет вид:
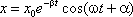
Каэффицент затухания - величина обратная пропорциональная времени в течении которого амплитуда уменшилась в е раз.
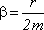
Время, по истечении которого амплитуда колебаний уменьшается в е раз, называется временем затухания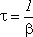 
|
|
|
За это время система совершает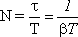 
колебаний.
Декремент затухания, количественная характеристика быстроты затухания колебаний,представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону.
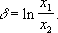
Логарифмическим декрементом затухания называется логарифм отношения амплитуд в моменты последовательных прохождений колеблющейся величины через максимум или минимум(затухание колебаний принято характеризовать логарифмическим декрементом затухания):
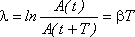
Он связан с числом колебаний N соотношением: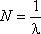 
Время релаксации - время в течении которого амплитуда затухающего колебания уменьшается в е раз.
Билет 14.
Вынужденные колебания. Полное дифференциальное уравнение вынужденных колебаний и его решение. Период и амплитуда вынужденных колебаний.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Второй закон Ньютона для т осциллятора (маятника) запишется в виде:
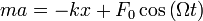
Если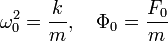 
и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение:
|
|
|
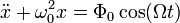
Общее решение однородного уравнения:
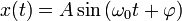
где A,φ произвольные постоянные
Найдём частное решение. Подставим в уравнение решение вида: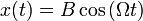 
и получим значение для константы:
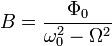
Тогда окончательное решение запишется в виде:
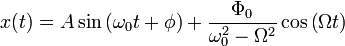
Характер вынужденных колебаний зависит от характера действия внешней силы, от ее величины, направления, частоты действия и не зависит от размеров и свойств колеблющегося тела.
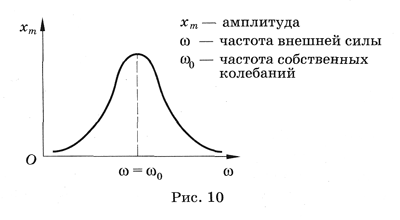
Зависимость амплитуды вынужденных колебаний от частоты действия внешней силы.
Период и амплитуда вынужденных колебаний:
Амплитуда зависит от частоты вынужденных колебаний, если частота равняет резонансной частоте, то амплитуда максимальнее. Так же зависит от коэффициента затухания, если он равнее 0, то амплитуда бесконечна.
Период связан с частотой, вынужденый колебания могут иметь любой период.
Билет 15.
Дата добавления: 2018-10-26; просмотров: 721; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!