Вынужденные колебания. Период и амплитуда вынужденых колебаний. Частота колебаний. Резонанс, резонансная частота. Семейство резонансных кривых.
+ Билет 14.
При совпадении частоты внешней силы и частоты собственных колебаний тела амплитуда вынужденных колебаний резко возрастает. Такое явление называют механическим резонансом.
Резона́нс— явление резкого возрастания амплитуды вынужденных колебаний.
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней частоты с внутренней частотой колебательной системы.
Резонансная частота – частота, в которой амплитуда максимальна (немного меньше собственной частоты)
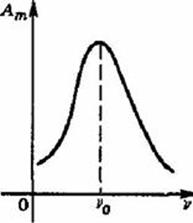
График зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной кривой.
В зависимости от коэффициента затухания получаем семейство резонансных кривых, чем коэффициент, меньше тем кривая больше и выше.
Билет 16.
Сложение колебаний одного направления. Векторная диаграмма. Биения.
Сложение нескольких гармонических колебаний одного направления и одинаковой частоты становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой.
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты:
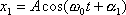
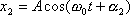
Представим оба колебания с помощью векторов A1и А2. Построим по правилам сложения векторов результирующий вектор А, проекция этого вектора на ось x равна сумме проекций складываемых векторов: 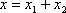
|
|
|
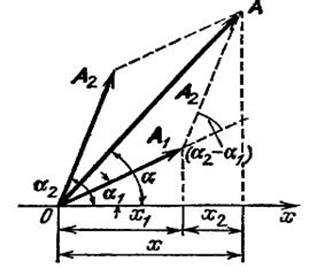
Поэтому, вектор A представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью как и векторы А1 и А2, так что сумма x1 и х2 является гармоническим колебанием с такой же частотой, амплитудой и фазой.Используя теорему косинусов получаем, что
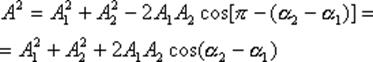
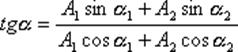
Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.
Биения - колебания с периодически меняющейся амплитудой, возникающие в результате наложения двух гармонических колебаний с несколько различными, но близкими частотами.
Билет 17.
Сложение взаимно перпендикулярных колебаний. Связь между угловой скоростью вращательного движения и циклической частотой. Фигуры Лиссажу.
Сложение взаимно перпендикулярных колебаний:
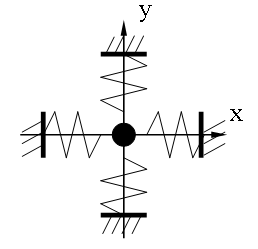
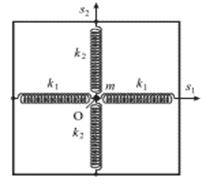
Колебания в двух взаимно перпендикулярных направлениях происходят независимо друг от друга:
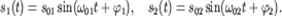
Здесь собственные частоты гармонических колебаний равны:
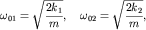
Рассмотрим траекторию движения грузов:
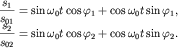
в ходе преобразований получим:
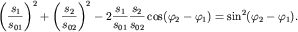
Таким образом, груз будет совершать периодические движения по эллиптической траектории. Направление движения вдоль траектории и ориентация эллипса относительно осей зависят от начальной разности фаз 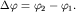
|
|
|
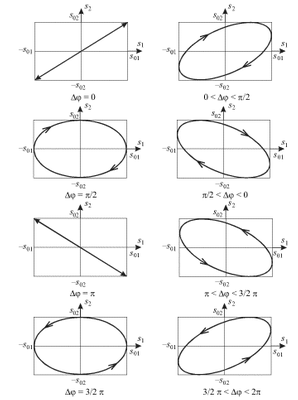
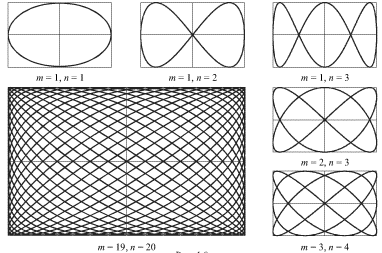
Если частоты двух взаимно-перпендикулярных колебаний не совпадают, но являются кратными, то траектории движения представляют собой замкнутые кривые, называемые фигурами Лиссажу. Отметим, что отношение частот колебаний равно отношению чисел точек касания фигуры Лиссажу к сторонам прямоугольника, в который она вписана.
Билет 18.
Дата добавления: 2018-10-26; просмотров: 398; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
