Динамика вращательного движения. Момент силы. Момент инерции. Теорема Штейнера.
Момент силы - величина, характеризующая вращательный эффект силы при действии её на твёрдое тело. Различают Момент силы относительно центра (точки) и относительно оси.
1.Момент силы относительно центра О величина векторная. Его модуль Mo = Fh, где F - модуль силы, a h - плечо (длина перпендикуляра, опущенного из О на линию действия силы)
С помощью векторного произведения момент силы выражается равенством Mo = [rF], где r - радиус-вектор, проведённый из О в точку приложения силы.
2.Момент силы относительно оси величина алгебраическая, равная проекции на эту ось.
Момент силы (крутящий момент; вращательный момент; вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
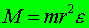
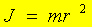
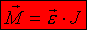
это выражение является вторым законом Ньютона для вращательного движения.
Оно справедливо только тогда:
а) если под моментом М понимают часть момента внешней силы, под действием которой происходит вращение тела вокруг оси - это тангенциальная составляющая.
б) нормальная составляющая из момента силы не участвует во вращательном движении, так как Mn старается сместить точку с траектории, и по определению тождественно равна 0, при r- const Mn=0, а Mz - определяет силу давления на подшипники.
Момент инерции - скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.
|
|
|
Момент инерции зависит от массы тела и от расположения частиц тела относительно оси вращения.
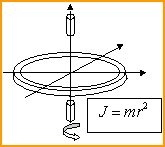
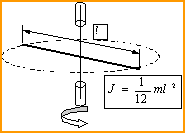
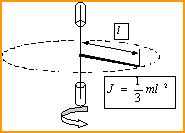
Тонкий обруч Стрежень (закреп. по середине) Стержень См.
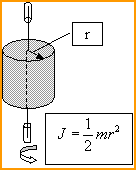
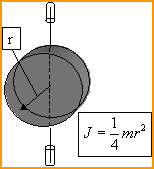
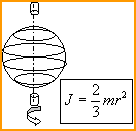
Однородный цилиндр Диск Шар. 
(справа картинка к пункту 2 в т. Штейнера)
Теорема Штейнера.
Момент инерции данного тела относительно, какой либо данной оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.
Согласно теореме Гюйгенса - Штейнера - момент инерции тела J относительно произвольной оси равен сумме:
1)момента инерции этого тела Jо, относительно оси, проходящий через центр масс этого тела, и параллельной рассматриваемой оси,
2) произведения массы тела на квадрат расстояния между осями.
Билет 10.
Момент импульса. Основное уравнение динамики вращательного движения (уравнение моментов). Закон сохранения моментов импульса.
|
|
|
Момент импульса - физическая величина, зависящая от того сколько массы вращается и как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Момент импульса относительно точки — это псевдовектор.
Момент импульса относительно оси — скалярная величина.
Момент импульса L частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса: L=[rP]
r - радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта.
P - импульс частицы.
L = rp sinА = p l ;
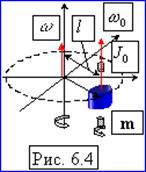
Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение:
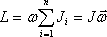 момент импульса тела относительно оси вращения.
момент импульса тела относительно оси вращения.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частей.
Уравнение моментов.
Производная по времени момента импульса материальной точки относительно неподвижной оси равна моменту силы, действующей на точку, относительно той же оси:
M=JE=J dw/dt=dL/dt
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
|
|
|
М=0
=> dL/dt=0 т.е. L=const
Билет 11.
Работа и кинетическая энергия при вращательном движении. Кинетическая энергия при плоском движении.
+Билет 8.
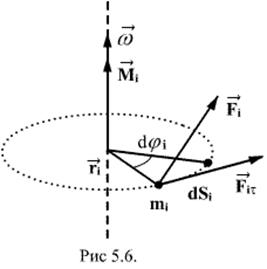
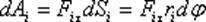
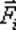 - внешняя силв приложенная к точке массой
- внешняя силв приложенная к точке массой 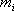
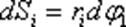 - путь который проходит масса за время dt
- путь который проходит масса за время dt
Но 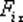 равна модулю момента
равна модулю момента 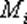 силы
силы 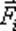 относительно оси вращения.
относительно оси вращения.
следовательно 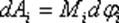
с учетом, что 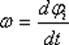
получим выражение для работы: 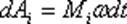
Работа вращательного движения равна работе затраченой на поворот всего тела.
Работа при вращательном движении идет на увеличении кинетической энергии:
dA=dT
Плоское (плоскопараллельным) движение - это такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.
Кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений:
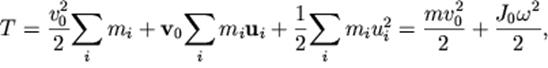
Билет 12.
Гармонические колебания. Свободные незатухающие колебания. Гармонический осциллятор. Дифференциальное уравнение гармонического осциллятора и его решение. Характеристики незатухающих колебаний. Скорость и ускорение в незатухающих колебаниях.
|
|
|
Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t).
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными.
Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.
Колебания называются гармоническими, если выполнятся следующие условия:
1) колебания маятника продолжаются бесконечно (так как нет необратимых преобразований энергии);
2) его максимальное отклонение вправо от положения равновесия равно максимальному отклонению влево;
3) время отклонения вправо равно времени отклонения влево;
4) характер движения вправо и влево от положения равновесия одинаков.
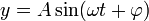
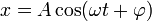
Х = Хm cos (ωt + φ0).
V= -A wo sin(wo+ φ)=A wo cos(wo t+ φ+П/2)
a= -A wo*2 cos(wo t+ φ)= A wo*2 cos(wo t+ φ+П)
x – смещение тела от положения равновесия,
xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия,
ω – циклическая или круговая частота колебаний,
t – время.
φ = ωt + φ0 называется фазой гармонического процесса
φ0 называют начальной фазой.
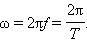
Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T
Частота колебаний f показывает, сколько колебаний совершается за 1 с.
Незатухающие колебания - колебания с постоянной амплитудой.
Затухающие колебания - колебания, энергия которых уменьшается с течением времени.
Свободные незатухающие колебания:
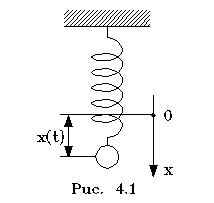
Рассмотpим пpостейшую механическую колебательную систему – маятник в не вязкой среде.
Запишем уpавнение движения согласно втоpому закону Ньютона:
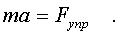
Запишем это уpавнение в пpоекциях на ось х.Пpоекцию ускорения на ось х пpедставим как втоpую пpоизводную от кооpдинаты х по вpемени.
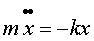
Обозначим k/m чеpез w2, и пpедадим уpавнению вид :
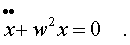
Где 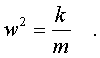
Решением нашего уpавнения является функция вида:
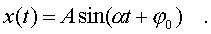
Гармонический осциллятор — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x(согласно закону Гука):
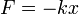
k — положительная константа, описывающая жёсткость системы.
1.Если F единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором.
2.Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором.
Дифференциальное уравнение гармонического осциллятора и его решение:
В качестве модели консервативного гармонического осциллятора возьмём груз массы m , закреплённый на пружине жёсткостью k. Пусть x - это смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила:
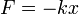
Используя второй закон Ньютона, запишем:
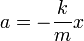
Обозначая 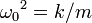 и заменяя ускорение
и заменяя ускорение 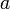 на вторую производную от координаты по времени
на вторую производную от координаты по времени 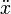 , напишем:
, напишем:
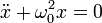
Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент ω0 называют циклической частотой осциллятора.
Будем искать решение этого уравнения в виде:
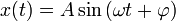
Здесь 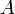 — амплитуда,
— амплитуда, 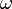 — частота колебаний (пока не обязательно равная собственной частоте),
— частота колебаний (пока не обязательно равная собственной частоте), 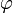 — начальная фаза.
— начальная фаза.
Подставляем в дифференциальное уравнение.
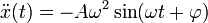
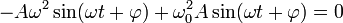
Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое — это означает, что груз покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. И остаётся условие на частоту колебаний:
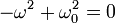
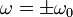
Отрицательную частоту можно отбросить, так как произвол в выборе этого знака покрывается произволом выбора начальной фазы.
Общее решение уравнения записывается в виде:
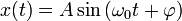
де амплитуда A и начальная фаза 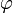 — произвольные постоянные.
— произвольные постоянные.
Кинетическая энергия записывается в виде:
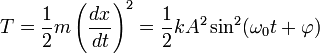
и потенциальная энергия есть
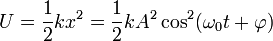
Характеристики незатухающих колебаний:
-амплитуда не меняется
-частота зависит от жесткости и массы (пружина)
Скорость незатухающих колебаний:
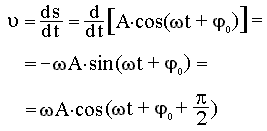
Ускорение незатухающих колебаний:
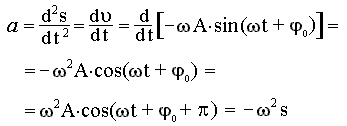
Билет 13.
Дата добавления: 2018-10-26; просмотров: 2118; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
