Распределение Больцмана. Распределение Максвлла-Больцмана. Барометрическая формула Больцмана.
Распределение Больцмана – распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия.
Закон распределения Больцмана:
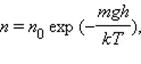
где n – концентрация молекул на высоте h,
n0 – концентрация молекул на начальном уровне h = 0,
m – масса частиц,
g – ускорение свободного падения,
k – постоянная Больцмана,
T – температура.
Распределение Максвелла-Больцмана:
равновесное распределение частиц идеального газа по энергиям (E) во внешнем силовом поле (напр., в поле тяготения); определяется функцией распределения:
f ~ e-E/kT
где E - сумма кинетической и потенциальной энергий частицы,
T - абсолютная температура,
k - постоянная Больцмана
Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:
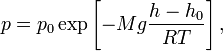
где p — давление газа в слое, расположенном на высоте h,
p0 — давление на нулевом уровне (h = h0),
M — молярная масса газа,
R — газовая постоянная,
T — абсолютная температура.
Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:
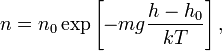
где m — масса молекулы газа, k — постоянная Больцмана.
Билет 27.
Первое начало термодинамики. Работа и теплота. Процессы. Работа совершаемая газом в различных изопроцессах. Первое начало термодинамики в различных процессах. Формулировки первого начала.
|
|
|
Билет 28.
Внутренняя энергия идеального газа. Теплоемкость идеального газа при постоянном обьеме и при постоянном давлении. Уравнение Майера.
Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем
Существует несколько эквивалентных формулировок первого начала термодинамики:
1) Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
2) Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе и не зависит от способа, которым осуществляется этот переход
3) Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале μ, и работы A', совершённой над системой внешними силами и полями, за вычетом работы A, совершённой самой системой против внешних сил
|
|
|
ΔU = Q A + μΔΝ + A`
Идеальный газ — газ, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Работа - При расширении работа газа положительна. При сжатии - отрицательна. Таким образом:
A' = pDV - работа газа (А' - работа газа по расширению)
A= - pDV - работа внешних сил (А - работа внешних сил по сжатию газа)
Теплота- кинетическая часть внутренней энергии вещества, определяемая интенсивным хаотическим движением молекул и атомов, из которых это вещество состоит.
Теплоемкость идеального газа - это отношение тепла, сообщенного газу, к изменению температуры δТ, которое при этом произошло.
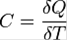
Внутренняя энергия идеального газа – величина, зависящая только от его температуры и не зависящая от объема.
Уравнение Майера показывает, что различие теплоемкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной R.
|
|
|
Для любого идеального газа справедливо соотношение Майера:
, 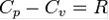
Процессы:
1.
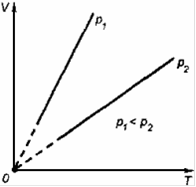
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении.
Работа, совершаемая газом при расширении или сжатии газа, равна
A = PΔV.
Количество теплоты, получаемое или отдаваемое газом:
Q = ΔU + A.
Теплоемкость:
для одноатомных газов 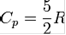 ,
,
для двухатомных газов 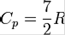 ,
,
для многоатомных газов Cp = 4R.
2.
Изохорный процесс— это термодинамический процесс, который происходит при постоянном объёме.
Работа, совершаемая газом при расширении или сжатии газа:
А=0
Количество теплоты, получаемое или отдаваемое газом:
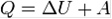
Теплоемкость:
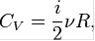
где i - число степеней свободы частиц газа
3.
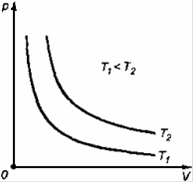
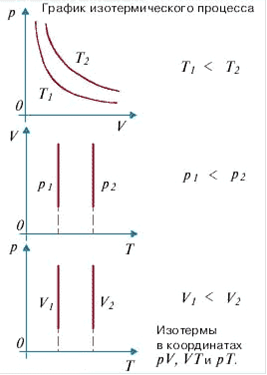
Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре.
Работа, совершаемая газом при расширении или сжатии газа:

Количество теплоты, получаемое или отдаваемое газом:
при постоянной температуре dU =0, поэтому все сообщаемое системе количество теплоты расходуется на совершение работы против внешних сил.
|
|
|
Теплоемкость:

Билет 29.
Адиабатный процесс. Уравнение адиабаты. Уравнение Пуассона. Работа в адиабатном процессе.
Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.
Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена системы со средой имеет вид:
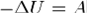
В адиабатическом процессе теплообмена с окружающей средой не происходит, т.е. δQ=0. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0.
Работа совершается газом за счет за счет изменения внутренней энергии Q=0, A=-DU
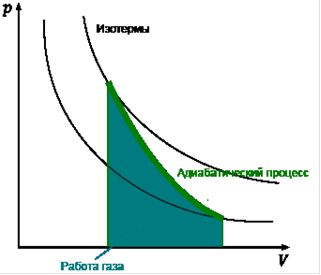
При адиабатическом процессе давление газа и его объем связаны соотношением:
pV*g=const, где g= Cp/Cv.
При этом справедливы следующие сотношения:
p2/p1=(V1/V2)*g, *g-степень
T2/T1=(V1/V2)*(g-1), *(g-1)-степень
T2/T1=(p2/p1)*(g-1)/g. *(g-1)/g -степень
Приведенные соотношения носят название уравнений Пуассона
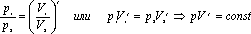
уравнение адиабатического процесса.(уравнение Пуассона) g- показатель адиабаты
Билет 30.
Дата добавления: 2018-10-26; просмотров: 1166; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
