Колебания груза на пружине. Математический и физический маятник. Характеристики колебаний.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению.
F (t) = ma (t) = –m ω2 x (t)
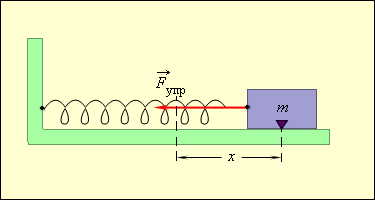
Fупр = –kx закон Гука.
Круговая частота ω0 свободных колебаний груза на пружине находится из второго закона Ньютона:
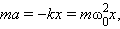
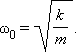
Частота ω0 называется собственной частотой колебательной системы.
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде:
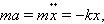
или
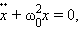 где
где 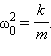
Решением этого уравнения являются гармонические функции вида:
x = xm cos (ωt + φ0).
Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость 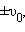
то 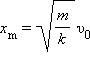
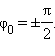
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести. Период малых колебаний математического маятника длины l в поле тяжести с ускорением свободного падения g равен
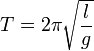
и мало зависит от амплитуды и массы маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела
Билет 19.
Волновой процесс. Упругие волны. Продольные и поперечные волны. Уравнение плоской волны. Фазовая скорость. Волновое уравнение и его решение.
Волна — это явление распространения в пространстве с течением времени возмущения физической величины.
В зависимости от физической среды, в которой распространяются волны, различают:
-волны на поверхности жидкости;
-упругие волны (звук, сейсмические волны);
-объёмные волны (распространяющиеся в толще среды);
-электромагнитные волны (радиоволны, свет, рентгеновские лучи);
-гравитационные волны;
-волны в плазме.
По отношению к направлению колебаний частиц среды:
-продольные волны (волны сжатия, P-волны) — частицы среды колеблются параллельно (по) направлению распространения волны (как, например, в случае распространения звука);
-поперечные волны (волны сдвига, S-волны) — частицы среды колеблются перпендикулярно направлению распространения волны (электромагнитные волны, волны на поверхностях разделения сред);
-волны смешанного типа.
По виду фронта волны (поверхности равных фаз):
-плоская волна — плоскости фаз перпендикулярны направлению распространения волны и параллельны друг другу;
-сферическая волна — поверхностью фаз является сфера;
-цилиндрическая волна — поверхность фаз напоминает цилиндр.
Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.
Поперечные волны, волны, распространяющиеся в направлении, перпендикулярном к плоскости, в которой ориентированы смещения и колебательные скорости частиц.
Продольные волны, волны, направление распространения которых совпадает с направлением смещений частиц среды.
Плоская волна, волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной к направлению её распространения, в каждый момент соответствуют одинаковые смещения и скорости частиц среды
Уравнение плоской волны:
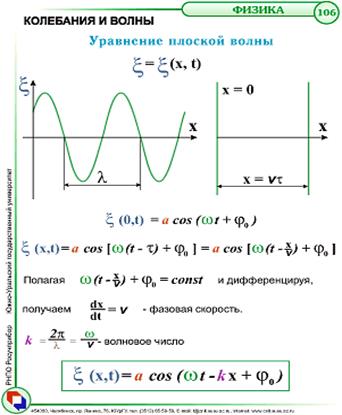
Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве вдоль заданного направления.
Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
Волновое уравнение и его решение:
Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением - дифференциальным уравнением в частных производных.
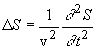 где
где 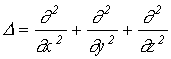
Решением уравнения является уравнение любой волны, которое имеет вид:
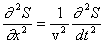
Билет 20.
Дата добавления: 2018-10-26; просмотров: 531; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
