Методика количественного контроля ПФ1 и ПФ2
Графический метод контроля основан на том, что при обобщенной скорости начального звена равной 1 и обобщенном ускорении равном нулю передаточные функции элементов механизма численно равны, соответственно, их скорости и ускорению, которые могут быть определены в результате построения планов скоростей и ускорений [4].
Поскольку построение планов вручную является трудоемкой и весьма неточной операцией, этот метод контроля мы использовать не будем, а рассмотрим численный метод контроля, который основан на следующих положениях.
На рис. 5.4 представлена линейная (или угловая) ПФ0 некоторого элемента механизма.
Рисунок 5.4 – ЛинейнаяПФ0точкизвена
С достаточной для инженерных расчётов точностью производная этой функции по ОК в точке, соответствующей положению начального звена k с абсциссой j1 k (или x1 k), может быть определена по известным значениям этой функции в нескольких соседних точках, расположенных с одинаковым шагом D j1 (или D x1). Сразу следует отметить, что операция численного дифференцирования может давать незначительные погрешности лишь для достаточно гладких функций, поэтому во всех случаях, когда это возможно, предпочтение следует отдавать аналитическим методам. Вместе с тем, расчёты показывают, что для подавляющего числа механизмов при оптимальном выборе параметров дифференцирования максимальные погрешности не превышают десятых, а то и сотых долей процента, что вполне приемлемо для большинства инженерных расчётов.
|
|
|
На точность численного дифференцирования влияют следующие факторы:
- число точек, значение передаточной функции в которых используется для определения производной в одной из них;
- шаг дифференцирования;
- положение расчётной точки относительно точек, используемых для определения производной.
Расчёты показывают, что минимальные погрешности достигаются при семиточечной схеме дифференцирования с шагом D j1=0,15...0,20, когда расчётная точка является средней среди заданных. Ниже приведены в матричной форме формулы для определения ПФ1 и ПФ2 в любой из семи заданных точек по известным значениям ПФ0 в этих точках.
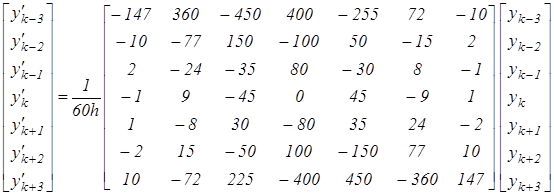 (5.1)
(5.1)
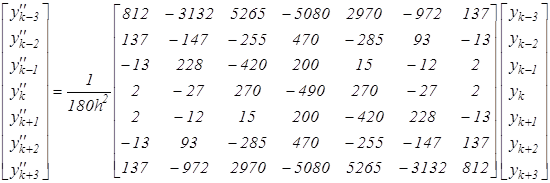 (5.2)
(5.2)
где h - шаг дифференцирования.
Напомним порядок раскрытия выражений, записанных в матричной форме. Величина ПФ в какой-либо из семи точек равна сумме произведений членов соответствующей строки квадратной матрицы на члены одностолбцовой матрицы. Например:
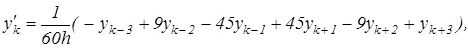 (5.3)
(5.3)
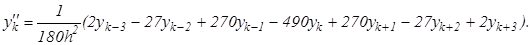 (5.4)
(5.4)
Следует ещё раз подчеркнуть, что для семи равноотстоящих точек более точными являются формулы для определения передаточных функций средней точки этого массива. Именно эти формулы и следует использовать для определения ПФ1 и ПФ2 для всех точек массива в количестве n, кроме трёх начальных (k=1, 2, 3) и трёх конечных (k=n−2, n−1, n). В этих случаях необходимо использовать формулы, соответствующие трём первым и трём последним строкам матриц. Для циклических механизмов, когда все передаточные функции являются периодическими функциями обобщённой координаты, во всех узлах можно использовать более точные формулы (5.3) и (5.4), так как к четырём первым узлам периода примыкают три последних узла предыдущего, а следовательно, и рассматриваемого периода, а к четырём последним узлам – три начальных узла следующего периода. В дальнейшем мы будем рекомендовать использовать приведенные формулы для непосредственного определения ПФ лишь в достаточно редких случаях отсутствия точных аналитических зависимостей и весьма широко – для контроля правильности точных аналитических расчётов.
|
|
|
Для численного дифференцирования передаточных функций с периодом 2  следует использовать процедуру Flux.
следует использовать процедуру Flux.
Её описание:
Flux (m : Integer, Var Yf, Yf_1, Yf_2 : Massiv),
где входные параметры:
m – число интервалов дифференцирования;
Yf – массив значений дифференцируемой функции в m+1 точках;
возвращаемые параметры:
Yf_1, Yf_2 − возвращаемые значения первой и второй производных этой функции.
|
|
|
При этом шаг дифференцирования 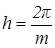 .
.
Для численного дифференцирования любых функций следует использовать процедуру Flux Univ.
Её описание:
Fluxuniv (n : Integer, dx : Real; Var Yf, Yf_1, Yf_2 : Massiv),
где n − число интервалов дифференцирования;
dx − шаг дифференцирования.
Если обобщённой координатой является угол, то dx следует вводить в радианах, если линейная координата, то в миллиметрах.
При использовании этой процедуры менее точных результатов можно ожидать в первых трёх и последних трёх точках интервала.
Рассмотрим методику использования тестирующих процедур.
Процедура Testpf предназначена для контроля правильности ПФ циклических механизмов, у которых начальным звеном является кривошип, делающий полный оборот. Эта процедура предусматривает ввод ПФ0, ПФ1 и ПФ2 какого-либо элемента механизма, найденных аналитически, расчет ПФ1 и ПФ2 по формулам (5.3) и (5.4) и сравнение передаточных функций, определенных двумя способами. Если относительная разница этих величин не превышает 0,1%, аналитические значения передаточных функций можно считать правильными, и на экране появляется соответствующее сообщение. Если же разница значений превышает 0,1%, на экран дисплея выводятся значения ПФ, найденных двумя способами. При этом возможны следующие варианты. Если на экран выводятся значения ПФ для всех положений начального звена, в программе, вероятнее всего, при обращении к соответствующей процедуре, допущена ошибка, которую следует найти и устранить.
|
|
|
В некоторых случаях на экран могут быть выведены нулевые значения передаточных функций. Это может произойти для положений, в которых теоретически величина ПФ1 или ПФ2 равна нулю. Однако в результате расчетов двумя способами получаются машинные нули, весьма малые числа, но отличающиеся друг от друга более чем на 0,1%, на что не следует обращать внимания.
Если же на экран выводятся значения ПФ в отдельных точках кривой, характеризуемых резким изменением передаточных функций, их аналитические значения, вероятнее всего, являются правильными.
В некоторых случаях может наблюдаться разница значений передаточных функций, найденных двумя методами в семи последовательных точках. Это может случиться, если функция претерпевает разрыв, например для графика угла оси звена механизма, где величина разрыва первого рода может равняться периоду тригонометрической функции, используемой для определения угла наклона звена. Такой разрыв на графике ПФ0 представлен на рис. 5.5.
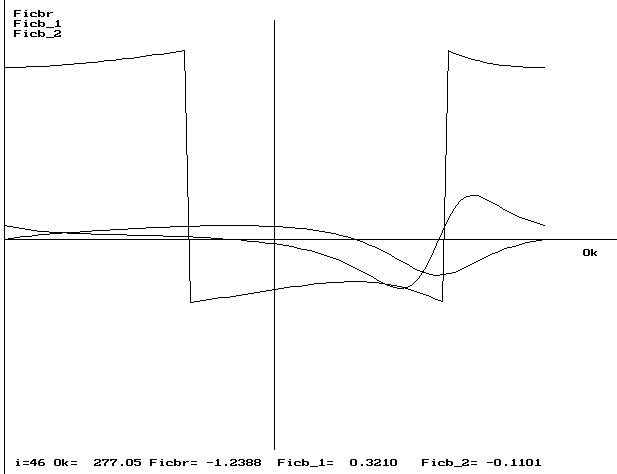
Рисунок 5.5 – График ПФ0
Этот разрыв можно устранить, прибавляя к отрицательным значениям угла период функции 2  , радиан.
, радиан.
Описание рассматриваемой процедуры:
Testpf (n : Integer; Yf, Yf_1, Yf_2 : Massiv; StrYf : String),
где n - число положений кривошипа, соответствующее одному обороту;
Yf, Yf_1, Yf_2 - формальные имена тестируемых массивов;
StrYf - формальное имя тестируемой функции.
Обратите внимание, что при тестировании углов их величину следует вводить в радианах.
Если начальное звено механизма совершает неполный оборот или движется поступательно, следует использовать процедуру Test Univ.
Ее описание:
Testuniv (m : Integer; Dx : Real; Yf, Yf_1, Yf_2 : Massiv; StrYf : String),
где, кроме переменных, таких же, как и в процедуре Testpf, Dx – шаг дифференцирования, который следует принимать в радианах при угловой обобщенной координате и в миллиметрах – при линейной обобщенной координате.
В этой процедуре расчет ПФ1 и ПФ2 выполняется по выражениям (5.1) и (5.2).
Дата добавления: 2018-10-26; просмотров: 265; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
