МЕТОДИКА ОПРЕДЕЛЕНИЯ ПФ0 СТРУКТУРНЫХ ГРУПП ВЫШЕ ВТОРОГО КЛАССА

⇐ ПредыдущаяСтр 8 из 16Следующая ⇒

Схемы некоторых структурных групп Ассура выше второго класса, то есть содержащих более двух звеньев, представлены на рисунках 1.1, 1.2 и 1.3.

Так как число таких структурных групп, отличающихся числом звеньев и сочетанием вращательных и поступательных КП, очень велико, актуальным является использование универсальной методики определения ПФ.

Возможные методы решения этой задачи рассмотрим на примере механизма, представленного на рис. 9.1 и используемого на металлургических предприятиях для отламывания чугунных чушек.

Рисунок 9.1 – Схема рычажного механизма чушколомателя

Если начальным звеном является кривошип 1, то остальные подвижные звенья механизма образуют четырёхзвенную структурную группу, представленную на рис. 9.2.

Рисунок 9.2 – Схема структурной группы

Рассмотрим метод, основанный на решении системы алгебраических уравнений. Для рассматриваемой структурной группы запишем шесть уравнений связей, содержащих шесть неизвестных (координаты точек В, С и Е):

(9.1)

Корни этой системы уравнений (x_B, y_B, x_C, y_C, x_E, y_E) являются значениями ПФ0 внутренних КП структурной группы. Решение системы нелинейных уравнений может быть выполнено численным методом Ньютона.

Рассмотрим реализацию этого метода на более простом примере расчёта структурной группы 2-го класса 1-го вида (рис. 9.3).

Рисунок 9.3 – Схема двухзвенной структурной группы

Пусть известны координаты осей внешних КП x_A, y_A, x_C, y_C, длины звеньев l_AB, l_CB. Следует определить координаты внутренней кинематической пары x_B, y_B. Из рис. 9.3 видно, что точка В лежит на пересечении окружностей с центром в точке А радиусом l_AB и с центром в точке С и радиусом l_CB.

Таким образом, координаты точки В являются корнями системы квадратных уравнений

(9.2)

Предположим, что известно некоторое приближённое значение корней системы и (первое приближение). Тогда точные значения корней системы можно представить в виде:

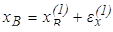; (9.3)

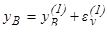где – поправки к приближённым значениям корней. Подставляя выражение (9.3) в левую часть уравнений системы (9.2), получим:

(9.4)

Разложим левые части уравнений (9.4) в ряд Тейлора по степеням e _x и e _y, ограничиваясь только линейными членами:

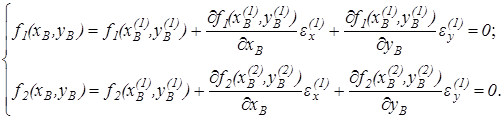(9.5)

Эти выражения представим в виде:

(9.6)

Тогда поправки и являются корнями системы двух линейных уравнений, так что:

(9.7)

где 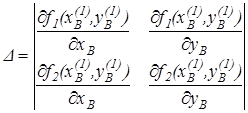. (9.8)

Рассмотрим реализацию этого метода на конкретном примере.

Пусть х_А=1; y_A=3, l_AB=5; x_C=8; y_C=4; l_BC=5.

Тогда уравнения (9.2) имеют вид

(9.9)

В качестве первого приближения корней принимаем 3,5, 7,5. Заметим, что точное значение корней х_В=4; y_B=7. Определим значения величин, которые входят в выражение (9.5):

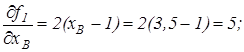
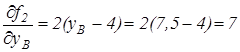тогда

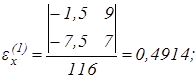
Тогда второе приближённое значение корней составит:

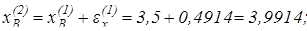
Выполняя следующее приближение, получим практически точные значения искомых корней.

Последовательное нахождение корней системы уравнений вида (9.1) можно представить в матричной форме. Совокупность аргументов х₁, х₂, .... х _n можно рассматривать как n-мерный вектор:

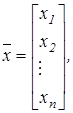
а совокупность функции f₁, f₂, .... f _n как n-мерный вектор:

Тогда ( p+1)-е приближённые значения корней могут быть получены из выражения

где - приближённые значения корней ;

- p-е приближения значений функции ;

- матрица, обратная матрице Якоби:

При реализации этого метода возникают трудности, связанные с отсеиванием корней в связи с многовариантностью сборки звеньев группы.

Следующий метод основан на том, что некоторые механизмы, содержащие группы выше второго класса, за счёт изменения начального звена можно преобразовать в механизм второго класса. Так, например, если в механизме, представленном на рис. 9.1, в качестве начального принять звено 5, то механизм преобразуется в механизм второго класса с формулой строения

(0-5) (3-4)₂ (1-2)₁.

Расчёт ПФ0 элементов этого механизма для различных положений звена 5 может быть выполнен по методике, изложенной в предыдущих разделах, с использованием стандартных процедур для групп Ассура второго класса. После этого необходимо получить значения ПФ0 элементов механизма для равноотстоящих положений кривошипа. Это может быть выполнено с помощью метода обратной интерполяции.

На рис. 9.4 представлена совокупность парных значений угла коромысла j₅ (или x) и угла кривошипа j₁ (или y), полученных для обращенного механизма 2‑го класса.

Рисунок 9.4 – Схема обратного интерполирования

Задача обратного интерполирования, то есть получения значений j₅ (или х) для равноотстоящих значений j₁ (или y) может быть решена с помощью интерполяционной формулы Лагранжа

, (9.10)

где x_i, y_i - координаты i-й узловой точки. Задавая y (или j₁) с одинаковым шагом, можно получить искомые значения x (или j₅). Однако при реализации этого метода возникают трудности, одна из которых заключается в определении крайних положений рассчитываемого звена. И, кроме того, не каждый механизм может быть преобразован в механизм второго класса.

Рассмотрим методику определения ПФ0, основанную на использовании стандартных процедур структурных групп второго класса пяти видов и идеях оптимизации, отличающуюся универсальным подходом к расчёту механизмов различной сложности и хорошей наглядностью, что особенно важно при выполнении учебных расчётов. Сущность методики рассмотрим на примере механизма третьего класса (см. рис. 9.1). Пусть необходимо определить положение звеньев группы для заданного положения кривошипа. С этой целью мысленно остановим точку А кривошипа, разрушим звено 5 и рассмотрим механизм, представленный на рис. 9.5.

Рисунок 9.5 – Схема фиктивного механизма

Если теперь звено 2 рассматривать как фиктивный кривошип, то звенья 3 и 4 образуют группу второго класса второго вида. Задаваясь углом j _AB, определяющим положение фиктивного кривошипа, можно, используя стандартные процедуры для групп второго класса, определить положение звеньев 3 и 4, а затем координаты точки С и расстояние CD. При правильном значении угла j _AB это расстояние должно равняться длине звена 5 - l_CD. Поиск нужного значения j _AB можно выполнить, используя идеи оптимизации. Для этого составляем целевую функцию в виде

. (9.11)

Варьируя j _AB, следует добиться выполнения условия ½ CF ½ £ D, где D - наперед заданная малая величина, например D=0,1 мм. Поиск нужного значения j _AB целесообразно выполнять методом половинного деления, сущность которого заключается в следующем. Сначала задаёмся величинами 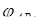, для которой CF₁>0, и , для которой CF₂<0, определяем середину интервала 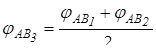и находим CF₃. После этого в качестве нового интервала принимаем тот, на границах которого значения CF имеют разные знаки. Процесс определения оптимального значения j _AB сходится достаточно быстро.

Мысленно разрушив звено 4 рассчитываемого механизма (см. рис. 9.1), можно прийти к фиктивному механизму другой структуры, как это показано на рис. 9.6.

Рисунок 9.6 – Схема фиктивного механизма

В этом случае полученный механизм включает фиктивный кривошип 2 и структурную группу второго класса первого вида (звенья 3 и 5). При этом необходимо найти такое значение угла фиктивного кривошипа j _AB, когда точка Е звена 3 оказывается на направляющей. В этом случае целевая функция имеет вид

. (9.12)

Два начальных значения угла j _AB следует назначить так, чтобы точка Е находилась по разные стороны направляющей ползуна.

Мысленно разрушив звено 5, как это показано на рис. 9.5, в качестве начального звена фиктивного механизма можно принять ползун 4. Тогда фиктивный механизм включает структурную группу первого вида (звенья 3 и 2), а целевая функция имеет вид, представленный формулой (9.11).

Дата добавления: 2018-10-26; просмотров: 285; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!