Наклонные и горизонтальные асимптоты
Определение. Прямая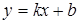 
называется наклонной асимптотой графика функции 
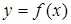при 
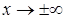,если эту функцию можно представить в виде 
, 
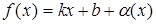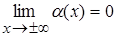, т. е. разность между ординатами точек кривой и асимптоты при 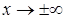есть бесконечно малая величина.
Теорема. Для того, чтобы график функции имел наклонную асимптоту, необходимо и достаточно, чтобы имели место соотношения:
, 
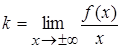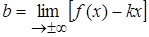, причем эти пределы могут быть неравными 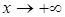при 
и при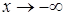 
. Если 
, 
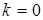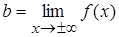, получаем горизонтальную асимптоту 
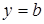. Таким образом, прямая 
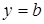является горизонтальной асимптотой кривой 
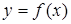, если 
.
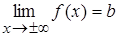Задача 2. Найти асимптоты графика функции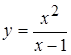 
.
Решение.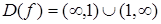 
. Вычислим 
=
= 
, 
.
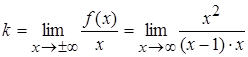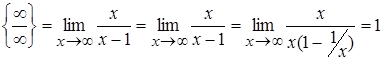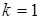Найдем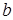 
: 
.
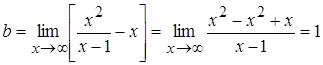Получим уравнение асимптоты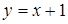 
; убедимся, что утверждение теоремы выполняется. Преобразуем функцию, выделив целую часть.
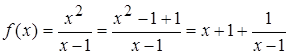, где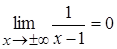 
, 
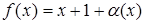
Кроме того, функция имеет вертикальную асимптоту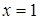 
, т. к.
, 
.
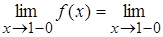
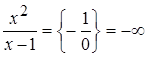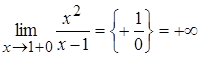Задача 3. Найти асимптоты графика функции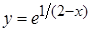 
.
Решение. Найдем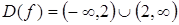 
. При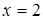 
функция 
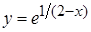терпит разрыв второго порядка, т. к.
.
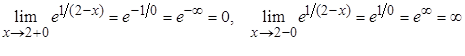Таким образом, 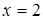является вертикальной асимптотой.
Найдем горизонтальные асимптоты.
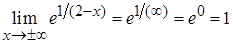, следовательно, 
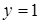является горизонтальной асимптотой.
Общая схема исследования функции
1. Найти область определения функции, исследовать ее поведение на границах области определения.
2. Найти точки разрыва и установить их характер с помощью односторонних пределов.
3. Исследовать периодичность, четность (нечетность), найти точки пересечения графика с осями координат.
|
|
|
4. Найти интервалы монотонности и экстремумы функции.
5. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции.
6. Найти асимптоты графика.
7. Построить график, используя результаты исследования.
Задача 4. Провести полное исследование и построить график функции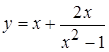 
.
1. Найдем область определения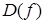 
. из условия 
, 
, 
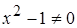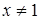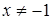, следовательно,
2. 
, 
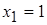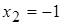– точки разрыва. Найдем односторонние пределы:
, 
,
, 
.
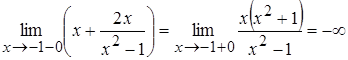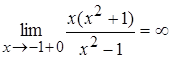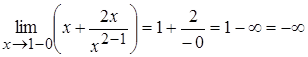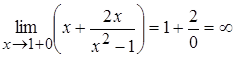Отсюда следует, что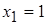 
и 
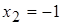– точки разрыва второго рода, и 
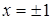– вертикальные асимптоты.
3. Для установления симметрии графика функции
найдем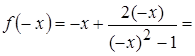 
= – 
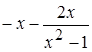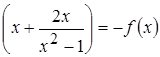, это означает, что 
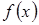– нечетная функция, и ее график симметричен относительно начала координат. Достаточно провести ее исследование для 
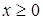. Очевидно, что функция не является периодической. Точка О (0,0) является единственной точкой пересечения с осями координат, т.к. 
.
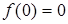4. Первая производная: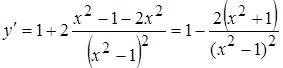 
,
Критические точки найдем из условий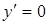 
, 
.
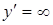а)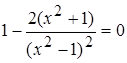 
, 
, 
, 
.
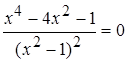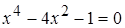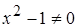Решая биквадратное уравнение, найдем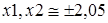 
.
б)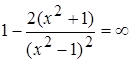 
, 
, 
, 
.
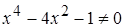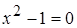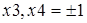Таким образом, критические точки функции: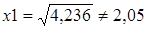 
, 
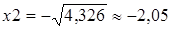, а точки 
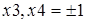не входят в область определения, следовательно, не являются критическими точками. Проверим критические точки на экстремум по первому признаку.
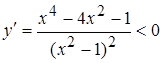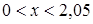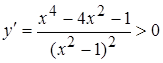, при 
, 
, при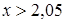 
Так как производная меняет знак при переходе через критическую точку, то в точке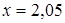 
функция имеет минимум. Составим таблицу.
|
|
|
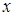
| 0 | (0, 1) | 1 | (1; 2.05) | 2,05 | (2,05,  )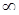
|
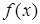
| 0 |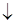 
| не сущ. |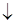
| (min) 3,4 | 
|
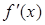
| 0 | – | не сущ. | – | 0 | + |
5. Найдем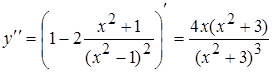 
. Критические
точки второго рода найдем из условия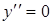 
, 
, 
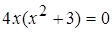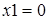; при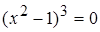 
,откуда 
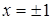. Так как 
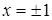не входят в область определения функции, то 
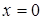единственная критическая точка. Проверим знак второй производной при переходе через точку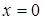 
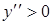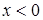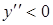при 
,
при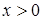 
. 
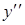меняет знак с «+» на «–», значит, 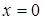– точка перегиба, и график меняет вогнутость на выпуклость при переходе через критическую точку. Итак, в (0, 1) функция выпукла, а в 
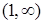– вогнута.
6. Найдем асимптоты. Наклонные асимптоты имеют вид: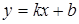 
;
= 
,
, 
,
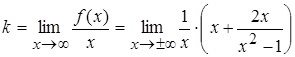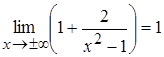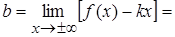
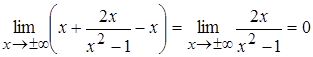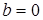отсюда уравнение наклонной асимптоты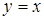 
. Горизонтальные асимптоты отсутствуют, а вертикальные были найдены в п. 2.
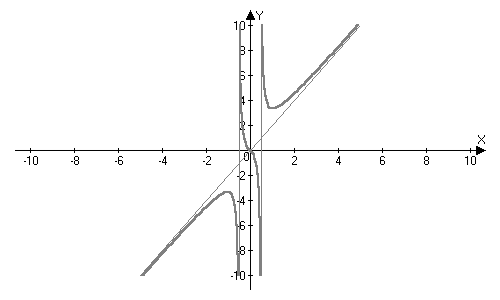
7. По результатам исследования построим график. Так как
функция нечетная, то можно построить график для 
и отобразить его симметрично начала координат.
 |
Дата добавления: 2018-09-23; просмотров: 201; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!