Возрастание, убывание функции. Точки экстремума

⇐ ПредыдущаяСтр 4 из 7Следующая ⇒

Определение 1 . Функция 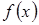называется возрастающей (убывающей) на некотором промежутке , если для любых этого промежутка ( ).

Функция возрастающая (убывающая) называется монотонной.

Теорема 1 . (Условие монотонности)

Если функция 1) определена на , 2) имеет конечную производную на , тогда, чтобы была возрастающей (убывающей) на , необходимо и достаточно, чтобы ( ).

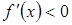Задача 1. Найти интервалы монотонности функции .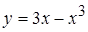

Решение. Область определения функции дифференцируема всюду в области определения: .

Решим неравенство , ,

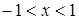-это интервал возрастания функции.

Соответственно неравенство справедливо для всех 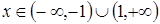– область убывания функции.

Определение 2. Точка называется точкой локального максимума (минимума), если в некоторой ее окрестности выполняется неравенство ( 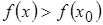) для всех 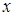этой окрестности.

Теорема 2 . (Необходимое условие существования экстремума)

Если 1) определена в окрестности точки , 2) дифференцируема в точке и 3) имеет в ней локальный экстремум, то .

Точки, в которых производная называются критическими.

Замечание. Функция может иметь экстремум и в точках, где первая производная не существует. Например: Функция непрерывна в точке , но не дифференцируема т. к. односторонние пределы не равны, значит, не существует в точке , но функция имеет минимум.

Теорема 3 . (Достаточное условие экстремума)

Если функция : 1) непрерывна в точке , 2) дифференцируема в некоторой области , 3) либо не существует и 4) при переходе через точку производная меняет знак, то – точка экстремума, причем, если производная слева от отрицательна, а справа положительна, то 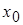– точка минимума; если слева от производная положительна (функция возрастает) а справа отрицательна (функция убывает), то – точка максимума.

Замечание: в промежутке между критическими точками производная сохраняет знак, следовательно, это промежутки монотонности.

Теорема 4 . (Исследование на экстремум с помощью второй производной или второе достаточное условие экстремума).

Если 1) в точке функция дифференцируема и ,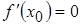
2) существует вторая производная, 3) в окрестности , то при функция имеет минимум, а при – максимум.

Итак, при исследовании функции на экстремум необходимо пользоваться правилами:

1. Найти первую производную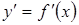

2. Найти критические точки , решив уравнения и .

3. Проверить, меняет ли знак первая производная при переходе через точку или установить знак второй производной , классифицировать экстремум.

4. Найти значение функции в экстремальных точках.

Задача. Исследовать на экстремум функцию .

Решение. Область определения ,

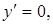
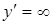, при . Это значение 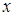не принадлежит области определения функции. Значит, – единственная критическая точка. Проверим знак первой производной слева и справа от нее.