Производная и правила дифференцирования
1. Пусть функция  =
=  получила приращение
получила приращение 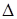
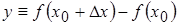 , соответствующее приращению аргумента
, соответствующее приращению аргумента 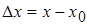 .
.
Определение . Если существует предел отношения приращения функции 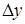 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 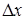 , при
, при 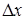 , стремящимся к нулю, т. е.
, стремящимся к нулю, т. е. 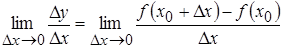 , то он называется производной функции
, то он называется производной функции 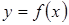 по независимой переменной
по независимой переменной  и обозначается
и обозначается 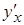 , или
, или 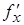 , или
, или  .
.
Функция, имеющая производную, называется дифференцируемой.
Задача 1. Используя определение, найти производные функций
а) 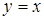 , б)
, б) 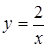 .
.
Решение: а) Дадим аргументу  приращение
приращение 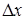 и найдем соответствующее значение функции
и найдем соответствующее значение функции 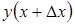 =
=  , теперь найдем
, теперь найдем 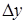
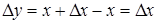 и составим отношение
и составим отношение 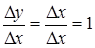 .
.
Осталось вычислить  ,
, 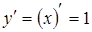 .
.
б) пусть аргумент  получил приращение
получил приращение 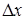 , новому значению аргумента соответствует значение функции
, новому значению аргумента соответствует значение функции 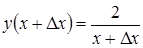 .
.
Найдем приращение 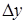 .
.  .
.
Тогда 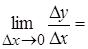
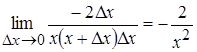 ,
,  .
.
Основные правила дифференцирования
Если 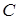 =соnst, а функции
=соnst, а функции 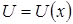 ,
, 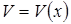 дифференцируемы, то
дифференцируемы, то
1.  4.
4. 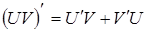 ;
;
2. 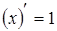 ; 5.
; 5. 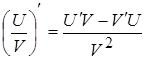 ;
;
3.  ; 6.
; 6. 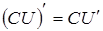 .
.
Таблица производных основных элементарных функций
1.  ; 10.
; 10.  ;
;
2. 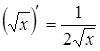 ,
, 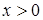 ; 11.
; 11. 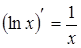 ;
;
3. 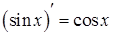 ; 12.
; 12. 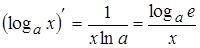 ;
;
4. 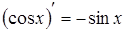 ; 13.
; 13.  ;
;
5. 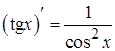 ; 14.
; 14. 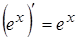 ;
;
6.  ; 15.
; 15. 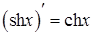 ;
;
7. 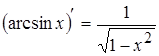 ; 16.
; 16. 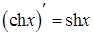 ;
;
8. 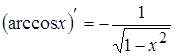 ; 17.
; 17. 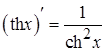 ;
;
9. 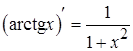 ; 18.
; 18. 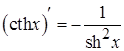 .
.
Правило дифференцирования сложной функции
|
|
|
Если 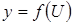 и
и 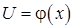 , т. е.
, т. е. 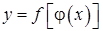 , где
, где  и
и 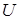 имеют производные, то
имеют производные, то 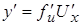 . Здесь
. Здесь 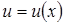 – промежуточный аргумент. Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций.
– промежуточный аргумент. Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций.
Задача 2. Найти производные функций:
а) 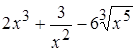 , б)
, б)  , в)
, в) 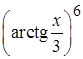 , г)
, г) 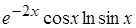 .
.
Решение: а) представим функцию в табличной форме как сумму степенных функций и затем только найдем производную.
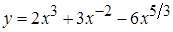 ,
,
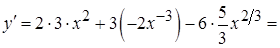
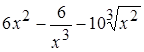 .
.
б) введем промежуточный аргумент и затем воспользуемся правилом дифференцирования сложной функции.
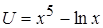 ,
, 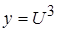 ,
, 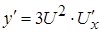 =3
=3 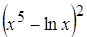
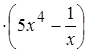 ;
;
в) пусть 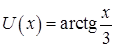 , где
, где 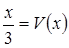 , тогда
, тогда  ,
,
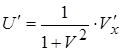 =
= 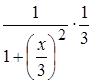 =
= 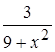 .
.
Окончательно: 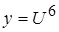 ,
, 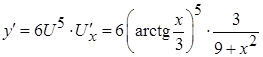 ;
;
г) правило 4 можно распространить на любое число сомножителей, если перемножаемые функции дифференцируемы.
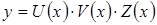 ,
,  , в данном случае
, в данном случае
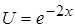 ,
, 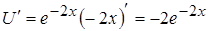 ,
, 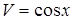 ,
, 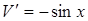 ,
,
 ,
, 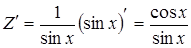 ,
,
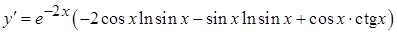 .
.
Дифференцирование сложной показательно-степенной функции  . Логарифмическое дифференцирование
. Логарифмическое дифференцирование
Пусть  и
и 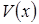 – дифференцируемые функции. Чтобы найти производную функции
– дифференцируемые функции. Чтобы найти производную функции  предварительно прологарифмируем ее по основанию
предварительно прологарифмируем ее по основанию 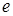 :
: 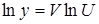 , теперь воспользуемся правилом 3 и 6
, теперь воспользуемся правилом 3 и 6
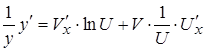 , откуда
, откуда  (1)
(1)
Задача 3. Найти производные функций а) 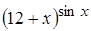 , б)
, б) 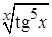
Решение: а) воспользуемся формулой (1): Пусть  ,
, 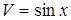 , найдем
, найдем 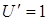 ,
,  и подставим в формулу (1):
и подставим в формулу (1):
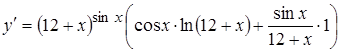
б) сначала прологарифмируем 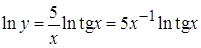 . Дифференцируя левую и правую части равенства, получим:
. Дифференцируя левую и правую части равенства, получим:
|
|
|
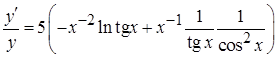 , теперь найдем
, теперь найдем 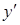
 =
= 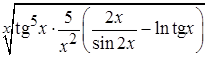 .
.
Метод, основанный на предварительном логарифмировании функции, не требует запоминания формулы и имеет более широкий спектр применения, в частности при дифференцировании большого количества сомножителей.
Задача 4. Найти производные функций:
а) 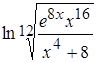 , б)
, б) 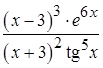 .
.
Решение: а) воспользуемся свойствами логарифмической функции:
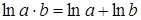 ,
,  ,
,  ,
,  .
.
Итак, 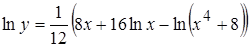 ,
,  ,
,
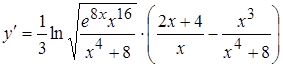 .
.
Дифференцирование функций, заданных параметрически
Если зависимость функции  и аргумента
и аргумента 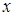 задана посредством параметра
задана посредством параметра 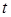 :
: 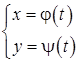 , то
, то 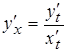 , или
, или 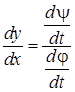 . (2)
. (2)
Пример 1. Найти 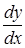 , если
, если 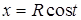 ,
, 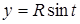 . Это параметрические уравнения окружности
. Это параметрические уравнения окружности 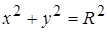 с центром в начале координат и радиуса
с центром в начале координат и радиуса 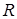 .
.
Решение. Находим  и
и 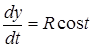 .
.
Отсюда  .
.
Пример 2. Найти 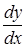
 от функции:
от функции: 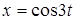 ,
, 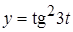 .
.
Решение:  ,
, 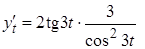 ,теперь по формуле (2)
,теперь по формуле (2)
найдем  .
.
Производная неявной функции
Пусть уравнение 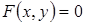 не разрешено относительно функции
не разрешено относительно функции 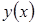 , т.е. функция
, т.е. функция 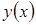 задана неявно. Чтобы найти производную
задана неявно. Чтобы найти производную  , надо продифференцировать левую и правую часть уравнения, учитывая, что
, надо продифференцировать левую и правую часть уравнения, учитывая, что  есть функция аргумента
есть функция аргумента 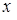 . Рассмотрим это правило на примерах.
. Рассмотрим это правило на примерах.
Пример 1. Найти 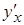 , если а)
, если а) 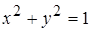 , б)
, б) 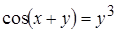 .
.
Решение: а)  , выразив
, выразив 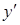 , получим
, получим  .
. 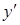 ;
;
б) дифференцируя обе части этого уравнения, получим уравнение относительно 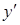 :
:  ,
, 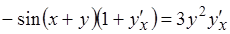 ;найдем теперь
;найдем теперь 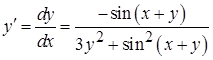 .
.
|
|
|
 |
Геометрический смысл производной
Здесь 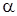 – угол наклона касательной к графику функции
– угол наклона касательной к графику функции 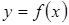 и точке
и точке  . Через две точки
. Через две точки 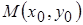 и
и  кривой
кривой 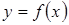 проведем секущую
проведем секущую 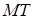 , ее угловой коэффициент
, ее угловой коэффициент  . Двигая точку
. Двигая точку 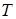 по кривой к точке
по кривой к точке 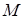 , мы будем поворачивать секущую вокруг точки
, мы будем поворачивать секущую вокруг точки  , в результате секущая стремится занять положение касательной, проведенной к графику в точке, а угол
, в результате секущая стремится занять положение касательной, проведенной к графику в точке, а угол 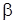 стремится к углу
стремится к углу 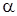 – наклона касательной, т.е.
– наклона касательной, т.е. 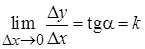 ,
,
где 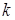 – угловой коэффициент касательной. Известное уравнение прямой
– угловой коэффициент касательной. Известное уравнение прямой 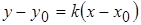 используем как уравнение касательной, проведенной к графику функции
используем как уравнение касательной, проведенной к графику функции  в точке
в точке  , с угловым коэффициентом
, с угловым коэффициентом 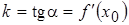 . Тогда уравнение касательной примет вид
. Тогда уравнение касательной примет вид
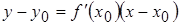 (3)
(3)
Задача. Найти уравнение касательной к графику функции
а) 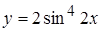 в точке
в точке  , б)
, б) 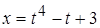 ,
, 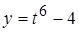 в точке
в точке 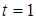 .
.
Решение. а) Сначала вычислим ординату точки касания 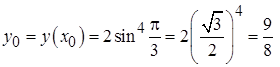 . Затем производную в точке
. Затем производную в точке 
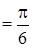 ,
,
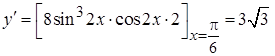 . Это угловой коэффициент касательной.
. Это угловой коэффициент касательной.
Подставим найденные параметры в уравнение (3)
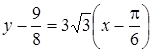 – искомая касательная;
– искомая касательная;
б) кривая задана параметрически; найдем координаты точки касания, подставив значение параметра в уравнение кривой:  ,
, 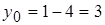 . Для отыскания углового коэффициента
. Для отыскания углового коэффициента 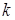 воспользуемся формулой
воспользуемся формулой 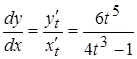 ,
, 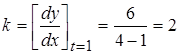 , теперь запишем уравнение касательной
, теперь запишем уравнение касательной  , или
, или 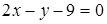 .
.
|
|
|
Дата добавления: 2018-09-23; просмотров: 172; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
