Дифференциал функции и формула приближенного вычисления
Определение . Дифференциалом функции называется величина, пропорциональная бесконечно малому приращению аргумента  , отличающаяся от соответственного приращения функции
, отличающаяся от соответственного приращения функции  на величину более высокого порядка.
на величину более высокого порядка.
По определению производной:  , откуда следует, что
, откуда следует, что  , где
, где  – бесконечно малая при
– бесконечно малая при  , т. е.
, т. е.  , тогда
, тогда  , где первое слагаемое и есть дифференциал
, где первое слагаемое и есть дифференциал
 ,
,  ,
,  . (4)
. (4)
Определение дифференциала позволяет использовать его в приближенных вычислениях, заменив вычисление функции ее дифференциалом. Рассмотрим приращение функции:  , или
, или 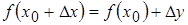 , тогда
, тогда
 . (5)
. (5)
Это и есть формула приближенного вычисления. Ошибка, получаемая при приближенных вычислениях, есть бесконечно малая высшего порядка, чем приращение аргумента, т. к.
 .
.
Задача 1. Найти дифференциалы функций:
а)  , б)
, б)  , в)
, в)  .
.
Решение: а)  , найдем сначала
, найдем сначала  и затем
и затем  ;
;
б)  ,
,  ;
;
в)  ,
, 
 .
.
Задача 2. Найти приращение и дифференциал функции  при
при  и
и  . Вычислить абсолютную и относительную ошибки, которые получаются при замене приращения функции ее дифференциалом.
. Вычислить абсолютную и относительную ошибки, которые получаются при замене приращения функции ее дифференциалом.
Решение  ,
, 

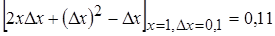 ;
;


Абсолютная ошибка  , относительная ошибка
, относительная ошибка
 .
.
Задача 3. Вычислить приближенно а) 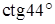 , б)
, б)  .
.
Решение. Чтобы воспользоваться формулой (5) надо составить функцию  (по виду вычисляемого выражения) и выбрать начальные условия так, чтобы
(по виду вычисляемого выражения) и выбрать начальные условия так, чтобы 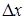 было мало, а
было мало, а 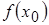 можно было легко подсчитать. В случае а) выбираем
можно было легко подсчитать. В случае а) выбираем  ,
,  ,
,
|
|
|
 ,
,  .
.
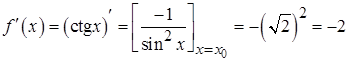 ,
,  ,
,
 ;
;
б) чтобы  было мало, необходимо извлечь целую часть корня, т. е.
было мало, необходимо извлечь целую часть корня, т. е.
 , откуда
, откуда  ,
,  ,
, 
 ,
,
 ,
,  ,
,  ,теперь вычислим приближенно
,теперь вычислим приближенно  :
:
 .
.
Производные и дифференциалы высших порядков
Определение 1. Производной второго порядка от функции  называется производная от производной первого порядка и обозначается символом
называется производная от производной первого порядка и обозначается символом  или
или  , или
, или  .
.
Пример. 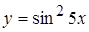 ,
, 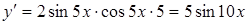 ,
,  .
.
Определение 2. Производной  -го порядка называется производная первого порядка от производной
-го порядка называется производная первого порядка от производной  -го порядка и обозначается
-го порядка и обозначается  или
или  , или
, или  .
.
Пример. 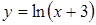 . Найти
. Найти  .
.
 ,
,  ,
,  !
!  ,
,
 !
! 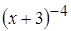 , используя метод математической индукции, запишем формулу производной
, используя метод математической индукции, запишем формулу производной  -го порядка
-го порядка 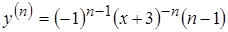 !
!
Определение 3. Дифференциалом высшего порядка функции называется дифференциал от дифференциала  -го порядка:
-го порядка:
 , в частности
, в частности 
 , здесь
, здесь  .
.
Пример:  . Найти
. Найти  .
.
 ,
, 
 ;
;
Тогда  .
.
Производная второго порядка от функции, заданной параметрически.
Если  , то производные
, то производные  ,
,  , последовательно могут быть вычислены по формулам:
, последовательно могут быть вычислены по формулам:
 =
=  ,
,  ,
,  и т. д.
и т. д.
Для производной второго порядка имеет место формула  .
.
Пример. Найти  от функции
от функции 
Решение. Найдем сначала  ,
,  ,
,
тогда  ,
,  .
.
Правило Лопиталя. Раскрытие неопределенностей при вычислении пределов
Теорема . Предел отношения двух бесконечно малых или двух бесконечно больших существует и равен пределу отношения их производных:
|
|
|
 , если выполняются условия:
, если выполняются условия:
1) функции 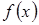 и
и  дифференцируемы в некоторой окрестности точки
дифференцируемы в некоторой окрестности точки  и
и 
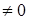 в этой окрестности.
в этой окрестности.
2) 
(или  ).
).
3) существует  конечный или бесконечный.
конечный или бесконечный.
Здесь  может быть числом или одним из символов:
может быть числом или одним из символов:  .
.
Задача 1. Вычислить пределы: а)  , б)
, б)  .
.
Решение. а) Подставив предельное значение аргумента  , получаем неопределенность
, получаем неопределенность  , т.к.
, т.к.  ,
,  и функции дифференцируемы.
и функции дифференцируемы.
Найдем  .
.
б) При  имеем неопределенность
имеем неопределенность  . Применим правило Лопиталя:
. Применим правило Лопиталя: 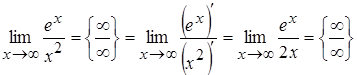 . Полученный предел снова представляет неопределенность вида
. Полученный предел снова представляет неопределенность вида  , применяя еще раз правило Лопиталя, найдем
, применяя еще раз правило Лопиталя, найдем  .
.
Другие виды неопределенностей 
 ,
,  ,
,  можно свести к виду
можно свести к виду  или
или  .
.
Задача 2. Найти предел 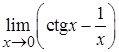 .
.
Решение. Подставим предельное значение аргумента, получим неопределенность  , которая легко сводится к частному:
, которая легко сводится к частному:

 =
=

=  .
.
Дата добавления: 2018-09-23; просмотров: 173; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
