Наибольшее и наименьшее значение функции.
Теорема Вейерштрасса . Если функция непрерывна на замкнутом промежутке  , то она достигает на нем наибольшее и наименьшее значения. Эти значения находятся либо на концах промежутка, либо в экстремальных точках.
, то она достигает на нем наибольшее и наименьшее значения. Эти значения находятся либо на концах промежутка, либо в экстремальных точках.
Правило отыскания наибольшего и наименьшего значения функции
1. Найти первую производную и все критические точки  , принадлежащие
, принадлежащие  .
.
2. Вычислить значения 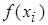 .
.
3. Вычислить значения функции на концах промежутка.
4. Сравнить все полученные значения функции 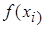 ,
, 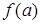 ,
, 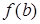 и выбрать среди них наибольшее и наименьшее.
и выбрать среди них наибольшее и наименьшее.
Задача. Найти наибольшее и наименьшее значения функции  на промежутке
на промежутке 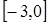 .
.
Решение. Необходимое условие экстремума 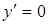 , поэтому
, поэтому 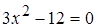 , а корни уравнения
, а корни уравнения  являются критическими точками, но промежутку принадлежит только
являются критическими точками, но промежутку принадлежит только 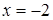 . Найдем теперь
. Найдем теперь 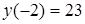 и на концах промежутка
и на концах промежутка  и
и 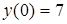 . Среди них самое большое 23, самое меньшее 7.
. Среди них самое большое 23, самое меньшее 7.
Выпуклость и вогнутость кривой. Точки перегиба
Пусть кривая задана функцией 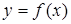 .
.
Определение 1. Кривая называется выпуклой вверх (вниз) на отрезке 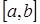 , если все точки кривой находятся ниже (выше) любой касательной к графику функции.
, если все точки кривой находятся ниже (выше) любой касательной к графику функции.
Определение 2 . Точка 
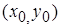 , отделяющая вогнутую часть от выпуклой, называется точкой перегиба графика функции
, отделяющая вогнутую часть от выпуклой, называется точкой перегиба графика функции  .
.
Теорема . Если функция 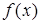 дважды дифференцируема на некотором промежутке, причем
дважды дифференцируема на некотором промежутке, причем 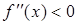 для любого
для любого 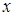 из этого промежутка, то на этом промежутке график функции выпуклый, если
из этого промежутка, то на этом промежутке график функции выпуклый, если 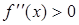 , то график вогнутый.
, то график вогнутый.
Из теоремы следует, что для нахождения промежутков (выпуклости) вогнутости надо найти вторую производную функции и определить промежутки, где она положительна (отрицательна). Необходимым условием существования точки перегиба является обращение в нуль второй производной или ее отсутствие в точке 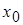 , то есть условие
, то есть условие  или
или  .
.
В случае выполнения одного из этих условий точка 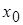 называется критической точкой второго рода.
называется критической точкой второго рода.
|
|
|
Достаточным условием того, что точка  - точка перегиба является смена знака второй производной при переходе через критические точки второго рода.
- точка перегиба является смена знака второй производной при переходе через критические точки второго рода.
Правило нахождения интервалов выпуклости, вогнутости и точек перегиба функции.
1. Указать область определения функции.
2. Найти критические точки второго рода, принадлежащие области определения функции.
3. Определить знак второй производной в каждом интервале области определения между соседними критическими точками.
4. По знаку 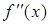 установить интервалы выпуклости, вогнутости и по смене знака второй производной в окрестности точки – наличие или отсутствие точки перегиба.
установить интервалы выпуклости, вогнутости и по смене знака второй производной в окрестности точки – наличие или отсутствие точки перегиба.
Асимптоты графика функции
Определение. Асимптотой графика функции называется прямая, к которой неограниченно приближается график функции при  или
или 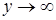 .
.
|
|
|
Различают вертикальные, горизонтальные и наклонные асимптоты.
1. Вертикальные асимптоты. Прямая  называется вертикальной асимптотой, если при
называется вертикальной асимптотой, если при 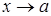 хотя бы один из односторонних пределов в точке
хотя бы один из односторонних пределов в точке  бесконечен, т.е.
бесконечен, т.е. 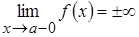 или
или 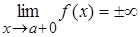 т. е. в точке
т. е. в точке  функция терпит разрыв второго рода.
функция терпит разрыв второго рода.
Задача. Найти вертикальные асимптоты функции  .
.
Решение. При  и
и 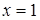 функция не определена. Найдем односторонние пределы
функция не определена. Найдем односторонние пределы 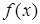 при
при 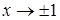 .
.
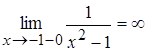 ,
, 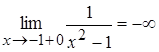 ;
; 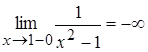 ,
,  .
.
Следовательно, 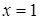 ,
,  вертикальные асимптоты графика.
вертикальные асимптоты графика.
Дата добавления: 2018-09-23; просмотров: 140; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
