Тема 10. АНАЛИЗ ИНТЕНСИВНОСТИ ДИНАМИКИ
Рядом динамики называется ряд чисел, характеризующих изменение явления во времени.
В зависимости от того, выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т.п.) или его величину за определенные интервалы времени (за сутки, декаду, месяц, год и т.п.) различают соответственно моментные и интервальные ряды динамики.
Уровни ряда динамики могут выражаться абсолютными, относительными и средними величинами.
Для анализа изменения социально-экономических явлений во времени применяются следующие показатели: абсолютный прирост, темп роста, темп прироста, абсолютное содержание 1% прироста. Их определяют базисным, цепным способами и осредняют.
Таблица 7.1
Формулы показателей анализа ряда динамики
| Показатели | Способ расчета | |
| базисный | цепной 
| |
| Абсолютный прирост | 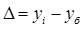
| 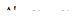
|
| Темп роста | 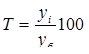
| 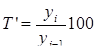
|
| Темп прироста | 
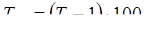 или или 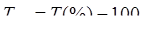
| 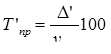
 или или 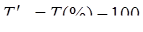
|
| Абсолютное содержание 1% прироста | 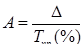 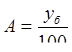
| 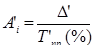 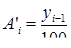
|
Условные обозначения: уi - уровень текущего периода; уi-1- уровень периода, предшествующего текущему; уб - базисный уровень (первый в ряду динамики).
В оценке динамики явлений большое значение имеют расчеты средних аналитических показателей, которые являются обобщающей характеристикой уровней, их абсолютной скорости и интенсивности изменения.
Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.
|
|
|
В интервальном ряду динамики с равностоящими во времени уровнями расчет среднего уровня ( 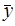 ) производится по формуле средней арифметической простой:
) производится по формуле средней арифметической простой:
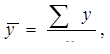
где n – количество хронологических дат.
Если интервальный ряд динамики имеет не равноотстоящие уровни, то средний уровень вычисляется по формуле:
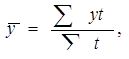
где t – количество периодов времени, в течение которых уровень не изменяется.
В моментных рядах динамики существует следующие варианты расчета среднего уровня:
1) дан ряд с равными интервалами времени между датами:
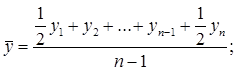
2) дан ряд с разными интервалами времени между датами и неизвестным характером изменений уровней между датами:
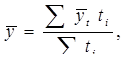
где 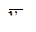 - средний уровень явления между двумя соседними датами.
- средний уровень явления между двумя соседними датами.
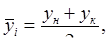
где  - начальный и конечный уровни на і-м интервале;
- начальный и конечный уровни на і-м интервале; 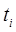 - длительность интервала времени между двумя соседними датами.
- длительность интервала времени между двумя соседними датами.
3) дан ряд с неравными интервалами времени между датами, но с исчер-пывающими данными об изменении явления между теми же датами:
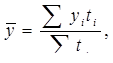
где yi – размер явления, который оставался неизменным в течение ti интервала времени.
Средний абсолютный прирост определяется по формуле:
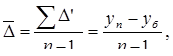
где 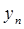 - конечный уровень ряда.
- конечный уровень ряда.
Средний темп роста рассчитывается по средней геометрической:
|
|
|
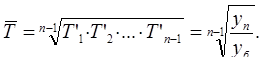
Средний темп прироста вычисляется так:
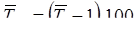 или
или 
Среднее абсолютное содержание 1% прироста рассчитывается по формуле:
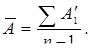
Одной из причин неверного отражения динамики явления слу-жит несопоставимость уровней ряда. Устранение несопоставимости уровней динамических рядов достигается использованием специальных приемов.
Смыкание рядов динамики применяется в случае несопоставимости уровней по территории, по кругу охватываемых объектов, по методике расчета показателей и др. Смыкание осуществляется двумя методами.
1. Использование коэффициентов пересчета. За год, когда возникла несопоставимость уровней, рассчитывается коэффициент, показывающий во сколько раз один уровень больше или меньше другого. Умножая на полученный коэффициент уровни ряда до изменения, приводят их к виду, сопоставимому с последующими уровнями.
2. Замена абсолютных уровней относительными, выраженными в базисных темпах роста. При этом уровень ряда за год, общий для сравниваемых рядов, принимается за 100%. Остальные уровни пересчитываются по отношению к этой базе сравнения, и получается новый ряд динамики, состоящий из относительных показателей.
При изучении рядов динамики возникает необходимость получения сравнительных характеристик направления и интенсивности роста одновременно развивающихся во времени явлений. Это достигается путем приведения рядов динамики к общему основанию. В этом случае данные о величине изучаемого показателя за год, принятый за базисный, принимают в каждом ряду за 100%, а уровни остальных лет относят к нему, получая базисные темпы роста.
|
|
|
Для оценки роста показателей сравниваемых параллельных рядов динамики за один и тот же период времени рассчитывают коэффициент опережения.
Его исчисляют как отношение базисных темпов роста (или средних годовых темпов роста) за одинаковые отрезки времени по двум динамическим рядам: 
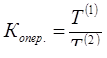 или
или 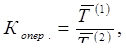
где 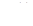 ,
,  - соответственно базисные и средние годовые темпы роста одного ряда динамики;
- соответственно базисные и средние годовые темпы роста одного ряда динамики; 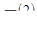 ,
,  - соответственно базисные и средние годовые темпы роста второго ряда динамики.
- соответственно базисные и средние годовые темпы роста второго ряда динамики.
При этом в качестве первого ряда динамики берется тот ряд, темпы роста для которого выше.
Для характеристики скорости изменения уровней одного и того же ряда динамики за отдельные периоды времени определяют коэффициент ускорения (замедления). По аналогии с коэффициентом опережения он рассчитывается на основании базисных или средних годовых темпов роста:
|
|
|

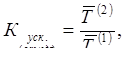
где 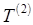 ,
, 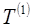 - базисные темпы роста уровней ряда динамики соответственно за второй и первый периоды одного и того же ряда динамики;
- базисные темпы роста уровней ряда динамики соответственно за второй и первый периоды одного и того же ряда динамики;  ,
,  - средние годовые темпы роста соответственно за второй и первый периоды одного и того же ряда динамики
- средние годовые темпы роста соответственно за второй и первый периоды одного и того же ряда динамики
Решение типовых задач
Пример 1. Провести анализ динамики прямых иностранных инвестиций в регион за 1999 – 2002гг.
Годы 1999 2000 2001 2002
Иностранные инвестиции, млн.долл.США 5,0 4,6 5,3 6,4
Решение
1. Для выражения абсолютной скорости роста (снижения) уров-ня ряда динамики рассчитывается абсолютный прирост 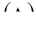 .
.
Базисный способ: 
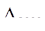 = 4,6 - 5,0 = -0,4млн.долл;
= 4,6 - 5,0 = -0,4млн.долл;
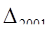 = 5,3 - 5,0 = 0,3млн.долл;
= 5,3 - 5,0 = 0,3млн.долл; 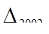 = 6,4 - 5,0 = 1,4млн.долл.
= 6,4 - 5,0 = 1,4млн.долл.
Следовательно, по сравнению с 1999г. иностранные инвестиции в регион в 2000г. снизились на 0,4 млн.долл., в 2001г. и 2002г. возросли соответственно на 0,3 и 1,4 млн.долл.
Цепной способ: 
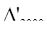 = 4,6 -5,0 = - 0,4млн.долл.;
= 4,6 -5,0 = - 0,4млн.долл.; 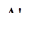 = 5,3 - 4,6 = 0,7млн.долл.;
= 5,3 - 4,6 = 0,7млн.долл.;  = 6,4 - 5,3 = 1,1млн.долл.
= 6,4 - 5,3 = 1,1млн.долл.
Следовательно, ежегодно по сравнению с предыдущим годом иностранные инвестиции изменялись так: в 2000г. снизились на 0,4млн.долл., в 2001г. возросли на 0,7млн.долл. и в 2002г. увеличи-лись на 1,1млн. долл.
2. Интенсивность изменения уровней ряда динамики оценивается с помощью темпа роста (Т).
Базисный способ: 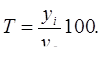
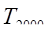 =
= 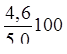 = 92,0%;
= 92,0%;
 =
= 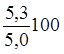 = 106,0%;
= 106,0%; 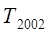 =
= 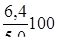 = 128,0% .
= 128,0% .
Таким образом, по сравнению с 1999г. иностранные инвестиции в 2000г. снизились в 0,92 раза, в 2001г. и в 2002г. увеличились соответственно в 1,06 и 1,28 раза.
Цепной способ: 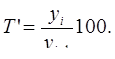
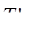 =
= 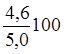 = 92,0%;
= 92,0%;
 =
= 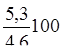 = 115,2%;
= 115,2%;  =
= 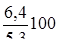 = 120,8%.
= 120,8%.
Следовательно, ежегодно по сравнению с предыдущим годом иностранные инвестиции изменялись так: в 2000г. их объем снизился в 0,92 раза, в 2001г. возрос в 1,152 раза, в 2002г. увеличился в 1,028 раза.
3. Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительном выражении определяется темп прироста (  ). В случае, когда уже исчислены темпы роста, темпы прироста целесообразно определять по следующим формулам.
). В случае, когда уже исчислены темпы роста, темпы прироста целесообразно определять по следующим формулам.
Базисный способ: 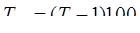 или
или 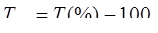
 = 92 - 100 = - 8%;
= 92 - 100 = - 8%; 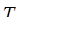 =106 - 100 = 6%;
=106 - 100 = 6%;
 = 128 - 100 = 28%.
= 128 - 100 = 28%.
Это означает, что иностранные инвестиции в регион по сравнению с 1999г. в 2000г. снизились на 8 %, в 2001г. возросли на 6 %, а в 2002г. увеличились на 28 %.
Цепной способ: 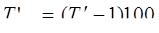 или
или 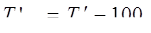
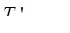 = 92 -100 = - 8%;
= 92 -100 = - 8%; 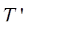 =1 15,2 -100 = 15,2%;
=1 15,2 -100 = 15,2%;
 = 120,8 -100 = 20,8%.
= 120,8 -100 = 20,8%.
Следовательно, ежегодно по сравнению с предыдущим годом иностранные инвестиции изменялись так: в 2000г. снизились на 8 %, в 2001г. возросли на 15,2 %, в 2001г. тоже увеличились на 20,8 %.
4. Определим показатель абсолютного значения 1% прироста. Его расчет на цепной основе будет следующим: 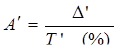
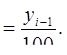
Для 2000г. этот показатель равен 5 : 100 = 0,050 млн.долл, для 2001г: 4,6 : 100 = 0,046млн.долл, для 2002г: 5,3 : 100 = 0,053млн.долл.
Таким образом, в 2000г. на каждый процент снижения инвестиций приходилось 0,05 млн.долл, в 2001г. на один процент прироста инвестиций приходилось 0,046 млн.долл., в 2002г. – 0,053 млн.долл. Итоги расчетов аналитических показателей изучаемого ряда динамики для наглядности рекомендуется представлять в таблице ( табл.7.2).
Таблица 7.2
Показатели анализа динамики иностранных
инвестиций в регион за 1999 – 2002 гг.
| Годы | Инстран-ные инвес-тиции,млн. долл США | Абсолютный прирост,млн. долл США | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста(цеп ной способ), млн.долл.США | |||
| базисный способ | цепной способ | базисный способ | цепной способ | базисный способ | цепной способ | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1999 | 5,0 | - | - | 100,0 | - | - | - | - |
| 2000 | 4,6 | -0,4 | -0,4 | 92,0 | 92,0 | -8,0 | -8,0 | 0,050 |
| 2001 | 5,3 | 0,3 | 0,7 | 106,0 | 115,2 | 6,0 | 15,2 | 0,046 |
| 2002 | 6,4 | 1,4 | 1,1 | 128,0 | 120,8 | 28,0 | 20,8 | 0,053 |
4. Данный ряд динамики по своему виду является интерваль-ным, поэтому средний уровень определяется по формуле:
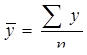 = =
= = 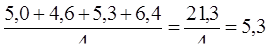 млн.долл.
млн.долл.
Это означает, что в среднем ежегодно иностранные инвестиции в регион составляли 5,3 млн.долл.
6. Средний абсолютный прирост определяется так:
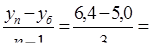 0,47 млн. долл. Это означает, что в среднем ежегодно иностранные инвестиции возрастали на 0,47 млн.долл.
0,47 млн. долл. Это означает, что в среднем ежегодно иностранные инвестиции возрастали на 0,47 млн.долл.
7. В нашем примере средний темп роста составит: 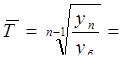
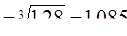 или 108,5%, т.е. в среднем ежегодно иностранные инвестиции возрастали в 1,085 раза.
или 108,5%, т.е. в среднем ежегодно иностранные инвестиции возрастали в 1,085 раза.
8. По данным нашего примера средний темп прироста будет таким: 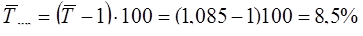 , т.е. в среднем ежегодно иностранные инвестиции увеличивались на 8,5%.
, т.е. в среднем ежегодно иностранные инвестиции увеличивались на 8,5%.
9. Рассчитаем среднее абсолютное значение одного процента прироста: 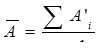
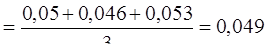 млн.грн. Следова-тельно, в среднем ежегодно на каждый процент прироста иностранных инвестиций приходилось 0,049 млн. грн.
млн.грн. Следова-тельно, в среднем ежегодно на каждый процент прироста иностранных инвестиций приходилось 0,049 млн. грн.
Пример 2. В I квартале отчетного года списочная численность работников предприятия составляла: на 01.01 – 32, на 01.02 - 36, на 01.03 – 27, на 01.04 - 34 человека. Определим среднюю списочную численность работников за квартал.
Решение
Приведенная в условии задачи информация представляет собой моментный ряд динамики с равными интервалами времени между датами, поэтому его средний уровень определяется по формуле:
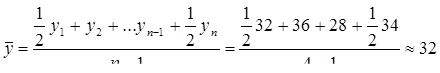 чел. Средняя списоч-ная численность работников банка за квартал составляла 32 человека.
чел. Средняя списоч-ная численность работников банка за квартал составляла 32 человека.
Пример 3. Задолженность предприятия по кредиту перед банком составила, млн. грн.: на 01.01 – 20, на 01.03 – 18 , на 01.07 – 14.
Определим среднюю сумму задолженности предприятия по кредиту перед банком за I полугодие.
Решение
Исходные данные представлены в виде моментного ряда с неравными интервалами времени между датами. При этом не известен характер изменения показателя между датами. По приведенным в условии задачи данным полугодие состоит из двух интервалов: I - c 01.01 по 01.03 – 2 месяца, II - с 01.03 по 01.07 – 4 месяца.
По каждому интервалу рассчитаем средний уровень по формуле: 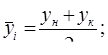
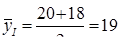 млн.грн., tI = 2мес,
млн.грн., tI = 2мес, 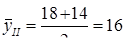 млн.грн.,
млн.грн.,
tII = 4 мес; 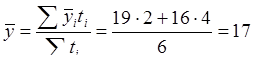 млн.грн.
млн.грн.
Таким образом, за I полугодие средняя сумма задолженности предприятия по кредиту перед банком составляла 17 млн. грн.
Пример 4. Известны следующие данные о движении денежных средств на расчетном счете предприятия в июле месяце: на начало месяца на счете было 100тыс.грн., 5 июля поступило еще 60тыс.грн., 22 июля списано 70тыс.грн. Какова средняя сумма денежных средств на счете предприятия в июле, если до конца месяца изменений на счете не наблюдалось?
Решение
Статистическая информация приведена в виде моментного ряда динамики с исчерпывающими данными об изменении явления, поэтому для расчета среднего уровня применяется формула:
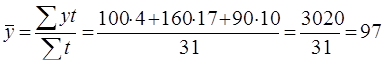 тыс.грн. Средняя сумма де-нежных средств на счете предприятия в июле составляла 97 тыс.грн.
тыс.грн. Средняя сумма де-нежных средств на счете предприятия в июле составляла 97 тыс.грн.
Пример 5. По имеющимся данным, характеризующие общий объем продукции промышленности в регионе (в фактически действовавших ценах), млн.грн., необходимо привести ряды динамики к сопоставимому виду.
| Годы | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| В старых границах региона | 28,0 | 29,4 | 30,0 | 31,5 | |||
| В новых границах региона | 36,2 | 37,4 | 38,3 | 40,0 |
Решение
1. Определим коэффициент пересчета уровней для 1999г., с этой целью сопоставим уровень производства этого года в старых и новых границах региона: 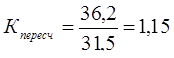 . Умножая на этот коэффициент показатели объема продукции первого ряда, получаем уровни, сопоставимые с уровнями второго ряда, млн. грн.: 1996г.– 28,0 · 1,15 = 32,2; 1997г.–24,9 · 1,15 = 33,8; 1998 г.– 30,0 · 1,15 = 34,5.
. Умножая на этот коэффициент показатели объема продукции первого ряда, получаем уровни, сопоставимые с уровнями второго ряда, млн. грн.: 1996г.– 28,0 · 1,15 = 32,2; 1997г.–24,9 · 1,15 = 33,8; 1998 г.– 30,0 · 1,15 = 34,5.
Получен ряд динамики с сопоставимыми уровнями объема продукции промышленности (в фактически действовавших ценах) в регионе (в новых границах):
Годы 1996 1997 1998 1999 2000 2001 2002
Сомкнутый ряд объема произ-
водства продукции, млн.грн. 32,2 33,8 34,5 36,2 37,4 38,3 40,0
2. Применяя другой способ смыкания, принимаем за 100% уровни 1999г. как для последующих, так и для предыдущих лет. Остальные уровни пересчитываются в % по отношению к этим уровням соответственно (до изменений – по отношению к 31,5, а после изменений – по отношению к 36,2). В результате получается сомкнутый ряд:
Годы 1996 1997 1998 1999 2000 2001 2002
Сомкнутый ряд объема про
изводства продукции в новых 88,9 93,3 95,2 100,0 103,3 105,8 110,5
границах региона, млн.грн.
Пример 6. Имеются данные о грузообороте железных дорог по двум странам, млрд. т. км:
Годы 1998 1999 2000 2001 2002
Страна А 158,7 164,9 172,8 180,4 185,0
Страна Б 65,0 66,8 70,4 68,5 66,8
Необходимо привести ряды динамики к одному основанию и рассчитать коэффициент опережения.
Решение
По абсолютным уровням приведенных рядов динамики затруднительно сделать оценку характера развития анализируемого показателя по разным странам. Приведем абсолютные уровни рядов динамики к общему основанию, приняв за постоянную базу сравнения 1998г., и получим данные, выраженные в % к 1998г.:
Годы 1998 1999 2000 2001 2002
Страна А 100,0 103,9 108,9 113,7 116,6
Страна Б 100,0 102,8 108,3 105,4 102,8
Из этих данных видно, что темпы роста грузооборота железных дорог в стране А превосходят темпы роста этого показателя в стране Б. Если в 2002г. грузооборот в стране А возрос по сравнению с 1998г. в 1,17 раза, то в стране Б он увеличился в 1,03 раза за то же время. При этом коэффициент опережения составил: 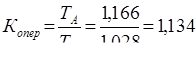 , т.е. гру-зооборот в стране А развивался за 1998-2002гг. в 1,13 раза быстрее, чем в стране Б.
, т.е. гру-зооборот в стране А развивался за 1998-2002гг. в 1,13 раза быстрее, чем в стране Б.
Дата добавления: 2018-09-23; просмотров: 1204; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
