Т ема 7 . Статистические показатели
При анализе статистической информации применяется система обобщающих показателей: абсолютных, относительных и средних величин.
Абсолютные величины выражают размеры, объемы явлений или процессов. Их получают непосредственно в результате статистического наблюдения, сводки и группировки данных, а также в результате специальных расчетов. К абсолютным показателям, например, относится площадь территории страны, объем промышленного производства, число предприятий и т.п.
Абсолютные статистические показатели всегда являются числами именованными. В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных и условно-натуральных, трудовых и стоимостных единицах измерения.
В международной практике используются такие натуральные единицы измерения, как тонны, килограммы, литры, километры, мили, баррели, штуки и т.д.
Условно-натуральные измерители используются в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства. Так, различные виды топлива переводят в условное топливо с теплотворной способностью в 7000 ккал/кг, мыло разных сортов – в условное мыло с 40 %-м содержанием жирных кислот и т.п. Перевод в условные единицы измерения осуществляется на основе коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению: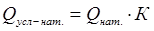 
.
|
|
|
Трудовые единицы измерения применяют, в основном, для определения единиц измерения рабочего времени (чел-час, чел-день).
В условиях рыночной экономики особое значение имеют стоимостные единицы измерения, позволяющие дать денежную оценку социально-экономическим объектам и явлениям.
Относительная величина - это обобщающий статистический показатель, характеризующий количественное соотношение двух величин в пространстве (между объектами), во времени (по одному и тому же объекту) или сравнения показателей разных свойств изучаемого объекта.
Относительные показатели получаются путем деления одной статистической величины на другую. В числителе всегда находится сравниваемый показатель, а в знаменателе – показатель, с которым производится сравнение (база сравнения). База сравнения выступает в качестве своеобразного измерителя. В зависимости от числового значения базы сравнения, результат отношения может быть выражен в коэффициентах, процентах, промилле (0/00), продецимилле (0/000), а также может быть числом именованным.
В статистике вычисляют следующие относительные величины:
|
|
|
1.Относительная величина планового задания - отношение величины показателя, устанавливаемого на планируемый период или обусловленной договором к его величине, достигнутой за предшествующий (базисный) период: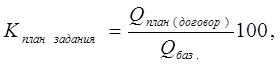 
| |
2. Относительная величина выполнения плана (нормы или договорных обязательств) - результат сравнения фактически достигнутого уровня показателя в текущем (отчетном) периоде с его плановым уровнем или нормативным, или уровнем, обусловленным договором. Если показатели заданы в абсолютном выражении:
,
где Q факт – фактический объем явления за отчетный период.
| |
| |
Рассмотренные относительные величины взаимосвязаны между собой: Кдинамики = Кплан. задания · Квып. плана
4. Относительная величина структуры характеризует состав совокупности, показывает, какой удельный вес (долю) во всей совокупности составляют ее части. Определяется как отношение размеров частей к целому: d = 
(100).
|
|
|
5. Относительная величина координации – соотношение частей целого между собой. За базу сравнения принимают одну из составных частей целого, а затем находят отношение всех частей к ней. Показывает, сколько единиц данной части целого приходится на 1, 10, 100, 1000 и т.п. единиц части, принятой за базу сравнения:
Kкоординации = K1 : K2 :... : K баз ,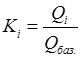 
,
где Qбаз– уровень, принятый за базу сравнения; Q1+ Q 2+...+ Qбаз=Qцелое
6. Относительная величина интенсивности характеризует сте-пень распространения или развития какого-либо явления в определенной совокупности, с ним связанной. Получается сопоставлением разноименных абсолютных величин, связанных в своем развитии, но относящихся к различным совокупностям (производительность труда, фондоотдача, рентабельность, демографические коэффициенты, социальные показатели и т.д.)
7. Относительная величина сравнения – отношение одноименных величин, относящихся к разным объектам или территориям, взятое, как правило, за одно и то же время. Выражается в коэффициентах.
Средняя величина – этообобщающий показатель, который характеризует типичный уровень варьирующего признака в расчете на единицу однородной совокупности. Она рассчитывается путем деления объема признаков на число единиц, обладающих данным признаком. Поэтому в общем виде формально это соотношение может быть представлено в форме агрегатной средней: 
|
|
|
где SM – объем явления или объем признака; n – объем совокуп-ности, т.е. число единиц, обладающих данным признаком.
В практике статистической обработки материалов возникают различные задачи. Для их решения требуются разные виды средних. В статистике вычисляют следующие виды средних величин:
1) среднюю арифметическую; 4) моду и медиану;
2) среднюю гармоническую; 5) среднюю хронологическую[2];
3) среднюю квадратическую; 6) среднюю геометрическую2.
Указанные средние величины можно объединить в две группы: степенные средние (средняя арифметическая, средняя гармоническая, средняя квадратическая и средняя геометрическая) и структурные средние (мода и медиана). Общая формула степенной средней имеет вид: 
,
где k - показатель степени средней.
При k = -1 - средняя гармоническая; k = 0 - средняя геометрическая;
k = 1 - средняя арифметическая; k = 2 - средняя квадратическая.
Признак, по которому находится средняя, называется осредняемым признаком и обозначается 
. Величины осредняемого признака у каждой единицы совокупности называются индивидуальными его значениями или вариантами. Обозначаются как x1, x2, x3, …xn.. Частота (повторяемость) индивидуальных значений признака – f (статистический вес).
Каждая средняя в зависимости от характера представления исходных данных рассчитывается двумя способами – как простая и как взвешенная. Если признак не сгруппирован, то применяется форма простой средней; если признак заранее сгруппирован, то применяется форма взвешенной средней.
Средняя арифметическая простая: 
,
где n – количество единиц совокупности (n = åf)
Средняя арифметическая взвешенная: 
,
где åxf = åM – объем явления.
Весами могут быть и частости, т.е относительные величины структуры (доли), выраженные в процентах или коэффициентах.
Тогда: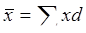 
(если d - доля, выраженная в коэффициентах):
(если d – в процентах)
В интервальных вариационных рядах значение признаков дано в виде интервалов “от … до …”. Для расчета средней в этом случае необходимо перейти к дискретному ряду, т.е. в каждом интервале найти среднее значение (x), а затем расчет выполнять по средней арифметической взвешенной: 
Средняя гармоническая – это величина, обратная средней арифметической. Применяется, если заданы объемы явлений (объемы признаков), но не известны частоты. По способу расчета средняя гармоническая бывает:
- простая, применяется, когда объемы признака (n) равны.
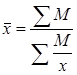- взвешенная, применяется, когда известны индивидуальные значения признака (х), но не заданы веса (f), которые входят сомножителем в известный объемный показатель (М = х f).
В практической работе часто возникает задача выбора формы средней величины между средней арифметической взвешенной и средней гармонической взвешенной. Для этого необходимо составить исходную схему расчета показателя:
.
Например, 
; 
. Если в условии задачи известен знаменатель исходной схемы, а неизвестен числитель, то применяется средняя арифметическая взвешенная. Если известен числитель, а знаменатель – нет, то используется средняя гармоническая взвешенная.
Средняя квадратическая применяется в тех случаях, когда варианты представляют собой отклонение заданных величин от нормы, от ГОСТа, от стандарта, т.е. от какой-то постоянной величины, в том числе и от среднего значения.
Рассчитывается: 
- простая; 
- взвешенная;
где f – количество единиц совокупности с тем или иным отклонением; х – отклонения (±)
Для характеристики структуры совокупности применяются особые показатели, которые называют структурными средними. Это мода и медиана. Эти показатели будут рассмотрены в теме 5.
Решение типовых задач
Пример 1. Валовой выпуск продукции отрасли составил в ба-зисном периоде 3500 тыс.грн. Планом на текущий период предус-мотрен выпуск на сумму 3800 тыс.грн., а фактическая его величина составила 3760 тыс.грн. Определите относительные величины плано-вого задания, выполнения плана и динамики.
Решение
1. Относительная величина планового задания:
= 1,086 или 108,6%.
Таким образом, планировалось увеличить в отчетном периоде по сравнению с базисным валовой выпуск продукции в 1,086 раза или на 8,6% (108,6% - 100%).
2. Относительная величина выполнения плана: 
= 
= 0,989 или 98,9%, т.е. план валового выпуска продукции вы-полнен на 98,9% или недовыполнен на 1,1% (98,9% -100%).
3. Относительная величина динамики: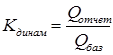 
| |
= 1,074 или 107,4%. В отчетном периоде по сравнению с базисным валовой выпуск продукции увеличился в 1,074 раза или на 7,4% (107,4% -100%). Взаимосвязь вычисленных показателей:
1,086 · 0,989 = 1,074.
Пример 2. Планом производства на текущий год по сравнению с базисным было предусмотрено снижение себестоимости продукции на 3%, а фактически она была снижена на 2,5%. Определите относительную величину выполнения плана по снижению себестоимости продукции в текущем году.
Решение
Показатели заданы в процентах. По их содержанию определяем значения относительных величин: относительная величина планового задания по снижению себестоимости составляет 97% или Кплан.задания= = 0,97, а относительная величина динамики – 97,5% или Кдинамики = 0,975. Тогда относительная величина выполнения плана через взаимосвязь показателей будет равна: 
| |
Пример 3. За отчетный год в стране было зарегистрировано 9710 промышленных предприятий (без малых предприятий и кооперативов), в том числе по формам собственности: частная – 37; коллективная – 7141; государственная – 2516; собственность международных организаций и юридических лиц других государств – 16.
Определите все возможные относительные величины.
Решение
1.Относительная величина структуры:
d = 
; dчаст = 
100 = 0,4%; dгосуд. = 
100 = 25,9%;
dкол. =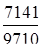 
100 = 73,5%; dмеждунар.= 
100 = 0,2%.
Наибольший удельный вес составляют предприятия коллективной формы собственности (73,5 %), на долю государственных предприятий приходится (25,9 %), малую долю составляют предприятия частные (0,4 %) и международные (0,2 %).
2. Относительная величина координации: примем за базу сравнения предприятия частной формы собственности: 
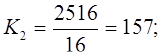
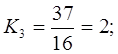Ккоордин.= 446 : 157 : 2 : 1.
Это означает, что на одно предприятие частной формы собственности приходится 446 предприятий коллективной формы собственности, 157 государственной и 2 предприятия частных.
Пример 4. По городу имеются данные за год, тыс.чел.: число родившихся - 24,92; среднегодовая численность населения – 2800. Определить относительную величину интенсивности, характеризую-щую рождаемость.
Решение
Определим коэффициент рождаемости:
Крожд. = 
1000 = 
1000= 90/00. Это означает, что в расчете на каждую тысячу человек населения за год рождается 9 детей.
Пример 5. Заработная плата бригады строителей по отдельным профессиям за месяц характеризуется следующими данными:
| Маляры | Штукатуры | Кровельщики | |||
| Заработная плата, грн | Число ра-бочих, чел | Заработная плата, грн | Число ра-бочих, чел | Заработная плата, грн | Число рабочих, чел |
| 300 | 1 | 320 | 2 | 330 | 3 |
| 310 | 1 | 336 | 2 | 342 | 5 |
| 317 | 1 | 340 | 2 | 355 | 2 |
Определить среднюю заработную плату рабочих: а) по каждой профессии; б) в целом по бригаде.
Решение
1. Среднюю зарплату маляров определим по средней арифметической простой, так как каждый признак встречается в совокупности один раз: 
; 
грн.
2.Среднюю зарплату штукатуров определим также по формуле средней арифметической простой, так как частоты равны между собой: 
грн.
3. Среднюю зарплату кровельщиков определим по формуле средней арифметической взвешенной, так как каждый признак встречается неодинаковое число раз:
грн.
4.Средняя зарплата всех рабочих бригады строителей может быть определена как средняя арифметическая взвешенная из групповых средних: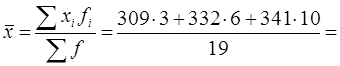 
333,1 грн.
Пример 6. Средняя выработка продукции на одного рабочего за смену в двух цехах завода, вырабатывающих однородную продукцию, характеризуется следующими данными:
| Бригада № | Цех № 1 | Бригада № | Цех № 2 | ||
| дневная выработ- ка продукции,шт | число ра-бочих,чел | дневная выработ- ка продукции,шт | объем произведен-ной продукции,шт. | ||
| I | 20 | 8 | IV | 38 | 418 |
| II | 30 | 11 | V | 36 | 432 |
| III | 35 | 16 | VI | 20 | 140 |
Определить среднюю дневную выработку продукции рабочих по каждому цеху.
Решение
Логическая схема расчета:
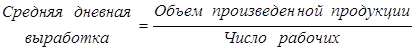
По первому цеху расчет произведем по средней арифметической взвешенной, поскольку по условию задачи известен знаменатель логической схемы расчета, т. е. число рабочих или частота появления признака: 
шт. По второму цеху – по средней гармонической взвешенной, т.к. известен числитель логической схемы расчета, т.е объем произведенной продукции:
шт.
Пример 7. Три предприятия производят электромиксеры. Себестоимость одного миксера составляет: на 1-ом предприятии 50 грн, на 2-ом 60 грн, на 3-ем 80 грн. Определить среднюю себестоимость миксера при условии, что общие затраты на производство миксера на всех предприятиях одинаковы.
Решение
Составим исходную схему расчета:
.
Так как общие затраты на всех предприятиях одинаковы, а значения признака (себестоимости) известны (x), расчет выполняем по средней гармонической простой:
= 60,6 (грн).
Пример 8. По данным о месячной зарплате 50-ти рабочих цеха определим среднюю зарплату:
| Группы рабочих по месячной зарплате, грн | Число ра-бочих, чел, f | Дискретный ряд, x | xf | Доля рабочих в коэф-тах, df | x df |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 400 - 420 | 2 | 410 | 820 | 0,04 | 16,4 |
| 420 - 440 | 4 | 430 | 1720 | 0,08 | 34,4 |
| 440 - 460 | 8 | 450 | 3600 | 0,16 | 72,0 |
| 460 - 480 | 20 | 470 | 9400 | 0,4 | 188,0 |
| 480 - 500 | 16 | 490 | 7840 | 0,32 | 156,8 |
| Итого: | 50 | - | 23380 | 1,0 | 467,6 |
Решение
Данные о месячной зарплате рабочих цеха представлены в виде интервального ряда распределения (гр.1, 2). Для расчета средней месячной зарплаты необходимо перейти к дискретному ряду распределения. Определим середину каждого интервала (x) и запишем результаты в гр.3. Затем выполним расчет в 2-х вариантах:
1. Используя в качестве весов численность рабочих (f) (гр.4):
грн.
2. Используя в качестве весов долю рабочих в коэффициентах (df) (гр.5, 6):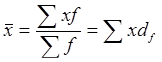 
; 
грн.
Пример 9. Члены садового товарищества постановили, что допустимый размер отклонения площади земельных участков от установленной нормы должен составлять 0,02 га. По следующим данным определите средний размер отклонения площади земельных участков от нормы:
| Отклонение, га | -0,03 | -0,02 | -0,01 | 0 | 0,03 | 0,04 | 0,05 | 0,06 | Итого |
| Число участков | 12 | 18 | 10 | 35 | 25 | 8 | 7 | 5 | 120 |
Решение
Для ответа на вопрос задачи вычислим среднюю квадратическую взвешенную, т.к. значения признака представлены в виде отклонений и предварительно сгруппированы: 
. Промежуточные вычисления выполним в таблице 4.1.
Таблица 4.1
Промежуточные расчеты для определения среднего размера
отклонения величины земельных участков от нормы
| Отклонения, га, x | Количество участков, f | x2 | x2f |
| 1 | 2 | 3 | 4 |
| - 0,03 | 12 | 0,0009 | 0,0108 |
| - 0,02 | 18 | 0,0004 | 0,0072 |
| - 0,01 | 10 | 0,0001 | 0,001 |
| 0 | 35 | 0 | 0 |
| 0,03 | 25 | 0,0009 | 0,0225 |
| 0,04 | 8 | 0,0016 | 0,0128 |
| 0,05 | 7 | 0,0025 | 0,0175 |
| 0,06 | 5 | 0,0036 | 0,018 |
| Итого | 120 | - | 0,0898 |
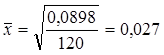га. Средний размер отклонения величины земельных участков от нормы в ту и другую сторону составляет 0,027 га.
Дата добавления: 2018-09-23; просмотров: 822; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!