Решение типовых задач (тема 5,6)
Пример 1. Имеются следующие данные о тарифных разрядах рабочих: 5, 4, 2, 1, 6, 3, 3, 4, 3, 2, 2, 5, 6, 4, 3, 5, 4, 1, 2, 3, 3, 4, 6, 6, 5, 1, 3, 4, 2, 5, 4, 3, 3, 4, 6, 4, 4, 3, 4, 3, 3, 4, 6, 3, 5, 4, 3, 3, 3, 4, 4, 5, 4, 3, 2, 5, 4, 2, 3, 5.
Постройте по этим данным: 1) ранжированный ряд рабочих по тарифному разряду; 2) ряд распределения рабочих по уровню квалификации: а) дискретный; б) интервальный, выделив 3 группы рабочих: низкой квалификации (1 - 2 разряды), средней квалификации (3 -4 разряды), высокой квалификации (5 - 6 разряды).
Решение
1.Для построения ранжированного ряда необходимо разряды всех рабочих распределить в порядке возрастания. Ранжированный ряд: 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6.
2. Ряд распределения рабочих по уровню квалификации:
а) дискретный:
Таблица 2.8
Дискретный ряд распределения рабочих по уровню
квалификации (разрядам)
| Разряды рабочих | 1 | 2 | 3 | 4 | 5 | 6 | Итого |
| Число рабочих, чел. | 3 | 7 | 18 | 17 | 9 | 6 | 60 |
б) интервальный ряд, образовав 3 группы рабочих по разрядам: [1 - 2], [3 - 4], [5 - 6].
Таблица 2.9
Интервальный ряд распределения рабочих по разрядам
| Группы рабочих по разрядам | Число рабочих,чел | Удельный вес рабочих,% |
| А | 1 | 2 |
| 1 - 2 | 10 | 17,0 |
| 3 - 4 | 35 | 58,0 |
| 5 - 6 | 15 | 25,0 |
| Итого | 60 | 100,0 |
Интервальный ряд распределения рабочих по уровню квалификации можно построить и по атрибутивному признаку.
|
|
|
Таблица 2.10
Распределение рабочих по уровню квалификации
| Уровень квалификации рабочих | Число рабочих, чел | Удельный вес рабочих, % |
| Низкая (1 - 2 разр.) | 10 | 17,0 |
| Средняя (3 - 4 разр.) | 35 | 58,0 |
| Высокая (5 - 6 разр.) | 15 | 25,0 |
| Итого | 60 | 100,0 |
Следовательно, наибольший удельный вес в данной совокупности занимают рабочие со средней квалификацией (58%), а наименьший – с низкой, их удельный вес составляет 17%. Данная группировка (табл. 2.10) по содержанию задачи является типологической, по характеру рассматриваемых признаков – атрибутивной, по числу группировочных признаков – простой.
Пример 2. Имеются следующие данные по 25 предприятиям обрабатывающей промышленности.
| Номер предприятия | Средняя списочная численность рабочих за отчетный год, чел. | Валовой выпуск продукции за отчетный год, млн.грн. |
| 1 | 2 | 3 |
| 1 | 280 | 1,4 |
| 2 | 480 | 4,8 |
| 3 | 420 | 3,7 |
| 4 | 503 | 6,1 |
| 5 | 710 | 9,4 |
| 6 | 1020 | 9,6 |
| 7 | 490 | 2,1 |
| 8 | 560 | 2,6 |
| 9 | 620 | 4,5 |
| 10 | 990 | 8,4 |
| 11 | 930 | 9,7 |
| 12 | 430 | 2,3 |
| 13 | 560 | 3,4 |
| 14 | 610 | 6,3 |
| 15 | 910 | 9,8 |
| 16 | 740 | 7,3 |
| 17 | 390 | 1,8 |
| 18 | 430 | 2,6 |
| 19 | 510 | 4,8 |
| 20 | 1250 | 16,1 |
| 21 | 340 | 1,3 |
| 22 | 390 | 2,3 |
| 23 | 250 | 21,3 |
| 24 | 960 | 2,9 |
| 25 | 490 | 3,4 |
|
|
|
1. Применяя метод аналитической группировки, выявите характер зависимости между изменением численности рабочих и выпуском продукции. При группировке по факторному признаку образуйте 4 группы с равными интервалами. 2. Выполните структурную группировку.
Решение
1. По содержанию показателей определяются факторный и результативный признаки: факторный (x) – среднесписочная численность рабочих, результативный (y) – валовой выпуск продукции.
2. Интервал группировки по факторному признаку при заданном числе групп (k = 4):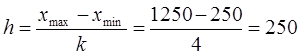 
чел.
где xmax и xmin – соответственно, максимальная и минимальная средне списочная численность рабочих, чел; k – количество групп.
Образуем следующие группы по численности рабочих, чел: [50 - 500]; [500- 750]; [750– 1000]; [1000– 1250]. Все вспомогательные расчеты целесообразно свести в таблице 2.11.
Таблица 2.11
Вспомогательные расчеты для выполнения аналитической группировки
| Группы предприятий по численности рабочих,чел | Номер пред-тия | Валовой выпуск продукции,млн.грн | Среднесписочная чис-ленность рабочих,чел | |||
| 1 | 2 | 3 | 4 | |||
| 250 - 500 | 1 | 1,4 | 280 | |||
| 2 | 4,8 | 480 | ||||
| 3 | 3,7 | 420 | ||||
| 7 | 2,1
| 490 | ||||
| 12 | 2,3 | 430 | ||||
| 17 | 1,8 | 390 | ||||
| 18 | 2,6 | 430 | ||||
| 21 | 1,3 | 340 | ||||
|
| 22 | 2,3 | 390 | |||
| 23 | 1,3 | 250 | ||||
| 25 | 3,4 | 490 | ||||
 Итого
|
| 27,0 | 4090 | |||
| 500 - 750 | 4 | 6,1 | 503 | |||
| 5 | 9,4 | 710 | ||||
| 8 | 2,6 | 560 | ||||
| 9 | 4,5 | 620 | ||||
| 13 | 3,4 | 560 | ||||
| 14 | 6,3 | 610 | ||||
| 16 | 7,3 | 740 | ||||
| 19 | 4,8 | 510 | ||||
| Итого
|
| 44,4 | 4813 | |||
| 750 - 1000 | 10 | 8,4 | 990 | |||
| 11 | 9,7 | 930 | ||||
| 15 | 9,8 | 910 | ||||
| 24 | 2,9 | 960 | ||||
| Итого
|
| 30,8 | 3790 | |||
| 1000 - 1250 | 6 | 9,6 | 1020 | |||
| 20 | 16,1 | 1250 | ||||
| Итого
|
| 25,7 | 2270 | |||
| Всего
|
| 127,9 | 14963 | |||
Итоговая таблица аналитической группировки будет иметь следующий вид:
Таблица 2.12
Зависимость между среднесписочной численностью рабочих
и валовым выпуском продукции
| Группы предприя-тий по среднесписочной численности рабочих, чел | Число предприя- тий, ед | Среднесписочная численность рабочих, чел. | Валовой выпуск продукции, млн. грн. | ||
| всего | в среднем на одно предприятие | всего | в среднем на одно предприятие | ||
| А | 1 | 2 | 3 | 4 | 5 |
| 250 - 500 | 11 | 4090 | 371 | 27,0 | 2,45 |
| 500 - 750 | 8 | 4813 | 601 | 44,4 | 5,55 |
| 750 - 1000 | 4 | 3790 | 947 | 30,8 | 7,70 |
| 1000 - 1250 | 2 | 2270 | 1135 | 25,7 | 12,85 |
| Итого | 25 | 14963 | 598 | 127,9 | 5,12 |
На основании выполненной аналитической группировки можно сделать вывод: увеличение среднесписочной численности рабочих приводит к росту валового выпуска продукции в среднем на одно предприятие, т.е. между этими показателями выявлена прямая зависимость.
|
|
|
3. Структурная группировка предназначена для изучения состава однородной совокупности. Для её выполнения необходимо рассчитать относительные величины структуры по анализируемому показателю. Представим структурную группировку предприятий по среднесписочной численности рабочих в таблице 2.13.
Таблица 2.13
Распределение предприятий по среднесписочной численности рабочих
| Группы предприятий по среднесписочной численности рабочих, чел | Число пред-приятий, ед | Среднесписочная чис- ленность рабочих | |
| всего,чел | удельный вес,% | ||
| А | 1 | 2 | 3 |
| 250 - 500 | 11 | 4090 | 27,3 |
| 500 - 750 | 8 | 4813 | 32,2 |
| 750 - 1000 | 4 | 3790 | 25,3 |
| 1000 - 1250 | 2 | 2270 | 15,2 |
| Итого | 25 | 14963 | 100,0 |
Вывод: в данной совокупности преобладают предприятия со среднесписочной численностью работающих 500 – 750 чел. (32,2%), наименьший удельный вес (15,2%), составляют предприятия с численностью 1000 – 1250 чел.
Пример 3. Имеются данные 15 фирм трех подотраслей промышленности о показателе выплаты дивидендов (%):
| Подотрасль промышленности | Показатель выплаты дивидендов, % | Тип фирмы | Количество фирм, ед |
| А | Б | В | 1 |
| 1. Производство детских игрушек | До 30 30 – 50 50 и выше | н с в | - 1 4 |
| 2. Производство животного масла | До 20 20 - 40 40 и выше | н с в | 1 2 - |
| 3. Производство хлопчатобумажных тканей | До 10 10 - 30 30 и выше | н с в | 2 4 1 |
Выполните типологическую группировку, выделив три группы фирм по уровню выплат дивидендов.
Решение
При выполнении типологической группировки все фирмы делят на 3 группы: с низким уровнем дивидендов (н), средним (с) и высоким (в) уровнем выплаты дивидендов. Объединим выделенные группы показателя выплаты дивидендов в три типа, независимо от подотрасли в таблице 2.14.
Таблица 2.14
Распределение фирм по уровню выплаты дивидендов
| Типы фирмы | Количество фирм | |
| единиц | удельный вес, % | |
| н | 3 | 20,0 |
| с | 7 | 46,7 |
| в | 5 | 33,3 |
| Итого | 15 | 100,0 |
Как видим, наибольший удельный вес занимают фирмы со средним уровнем выплаты дивидендов. На их долю приходится 46,7 %.
Пример 4. В группе студентов второго курса обучаются 24 человека, из них 20 студентов женского пола и 4 – мужского. Постройте альтернативный ряд распределения.
Решение
Пол студента – альтернативный признак, поэтому образуем две группы и определим удельный вес каждой группы в общей численности студентов. Результаты группировки представим в таблице 2.15.
Таблица 2.15
Распределение студентов группы второго курса по полу
| Группы студентов по полу | Число студентов, чел. | Удельный вес в общей численности, % |
| Женский | 20 | 83,3 |
| Мужской | 4 | 16,7 |
| Итого | 24 | 100,0 |
Таким образом, на долю студентов женского пола приходится 83,3 %, а на долю мужского – 16,7 %.
Пример 5. Имеются данные о распределении филиалов банка “Маяк” по размеру прибыли:
| I регион | II регион | ||||
| Номер груп- пы | Группы филиалов банка по размеру прибыли, тыс.грн. | Удельный вес банков, в % к итогу | Номер груп- пы | Группы филиалов банка по размеру прибыли, тыс. грн. | Удельный вес банков, в % к итогу |
| I | До 100 | 4,3 | I | До 50 | 1,0 |
| II | 100-200 | 18,3 | II | 50-70 | 1,0 |
| III | 200-300 | 19,5 | III | 70-100 | 2,0 |
| IV | 300-500 | 28,2 | IV | 100-150 | 10,0 |
| V | Свыше 500 | 29,7 | V | 150-250 | 18,0 |
| VI | 250-400 | 21,0 | |||
| VII | 400-500 | 23,0 | |||
| VIII | Свыше 500 | 24,0 | |||
| Итого | 100,0 | Итого | 100,0 | ||
Сравните структуру филиалов банка “Маяк” по размеру прибыли, за основу приняв интервалы группировки I-го региона.
Решение
Приведенные данные не позволяют произвести сравнение распределения отделений банка “Маяк” в двух регионах по размеру прибыли, так как несопоставимы по интервалам группировки.
По второму региону произведем вторичную группировку филиалов банка путем пересчета частот, т.е. удельного веса банков. В первую вновь образованную группу филиалов второго региона с размером прибыли до 100 тыс. грн. войдут первые три группы филиалов, удельный вес которых равен 4% (гр.2 табл.2.16). Во вторую группу, т.е. в интервал от 100 до 200 тыс. грн. войдет четвертая группа филиалов, т.е. 10%, а также часть пятой группы.
Для определения удельного веса этой части рассчитываем, сколько частот приходится на единицу интервала, и умножаем на размер признака, который должен перейти в новый интервал, т.е.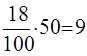 
. И тогда доля второй группы после пересчета составит 19 (10 + 9). В последнюю, пятую группу филиалов банка, с размером прибыли свыше 500 тыс. грн. войдет вся восьмая группа, на долю которой приходится 24% филиалов. Представим расчеты в таблице 2.16.
Таблица 2.16
Расчетная таблица вторичной группировки филиалов банка “Маяк”
| Номер груп-пы | I регион | II регион | ||
| Группы филиалов банка по размеру прибыли, тыс.грн | Удельный вес банков, в % к итогу | Группы филиалов банка по размеру прибыли, тыс.грн | Удельный вес банков, в % к итогу | |
| 1 | 2 | 3 | 4 | 5 |
| I | До 100 | 4,3 | До 100 | 1 + 1 +2 = 4.0 |
| II | 100 - 200 | 18,3 | 100 - 200 |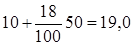 
|
| III | 200 - 300 | 19,5 | 200 - 300 |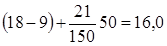 
|
| IV | 300 - 500 | 28,2 | 300 - 500 | (21-7) + 23 =37,0 |
| V | Свыше 500 | 29,7 | Свыше 500 | 24 |
| Итого | 100,0 | Итого | 100,0 | |
В результате вторичной группировки получим следующие сопоставимые данные (табл.2.17)
Таблица 2.17
Распределение филиалов банка “Маяк” по размеру
прибыли в двух регионах
| Номер группы | Группы филиалов банка по размеру прибыли, тыс. грн | Удельный вес группы филиалов банка в % к итогу | |
| I регион | II регион | ||
| А | Б | 1 | 2 |
| I | До 100 | 4,3 | 4,0 |
| II | 100 - 200 | 18,3 | 19,0 |
| III | 200 - 300 | 19,5 | 16,0 |
| IV | 300 - 500 | 28,2 | 37,0 |
| V | Свыше 500 | 29,7 | 24,0 |
| Итого | 100,0 | 100,0 | |
Пример 6. Имеются данные о величине доходов 10 малых предприятий.
| Номер предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Размер дохода, тыс.грн | 180 | 595 | 1191 | 850 | 211 | 1100 | 600 | 95 | 603 | 15 |
Выполните группировку малых предприятий с прогрессивно возрастающими в арифметической прогрессии интервалами.
Решение
1. По формуле Стерджесса определим количество групп:
k = 1 + 2,233 lg n; k = 1 + 2,233 · 1,3 = 3.
Величина первого интервала будет равна:
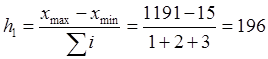тыс. грн.
3. Определим последующие интервалы: h2 = 2h;
h2 = 2 ·196 = 392 тыс.грн; h3 = 3h; h3 = 3 · 196 = 588 тыс.грн
4. Сформируем группы предприятий по размеру дохода, тыс. грн.: [15 - 211], [211 - 603], [603 – 1161].
5. Результаты группировки представим в таблице 2.18.
Таблица 2.18
Группировка малых предприятий по размеру дохода
| Группы предприятий по размерам доходов, тыс.грн | Кол-во предприятий, ед |
| 15-211 | 3 |
| 211-603 | 3 |
| 603-1191 | 4 |
| Итого | 10 |
Дата добавления: 2018-09-23; просмотров: 9940; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!