I. Проверка домашнего задания.
1. № 669 вынести решение на доску.
2. Решить устно:
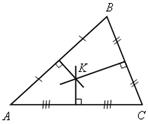
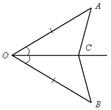
1) Докажите, что SАОС = SВОС.
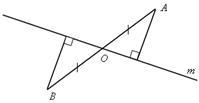
2) Прямая m пересекает отрезок АВ в его середине. Докажите, что концы отрезка АВ равноудалены от прямой m.
II. Изучение нового материала.
1) Доказательство теоремы.
2) Доказательство следствия из теоремы.
Изложить лучше самому учителю в виде небольшой лекции.
III. Закрепление изученного материала.
Решить №№ 674, 675, 676 (а).
№ 674.
Решение
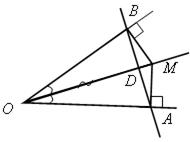
| 1)  АОМ = АОМ =  ВОМ (по гипотенузе и острому углу), тогда АО = ОВ.
2) ВОМ (по гипотенузе и острому углу), тогда АО = ОВ.
2)  АОВ – равнобедренный, поэтому биссектриса ОD является высотой, то есть DО АОВ – равнобедренный, поэтому биссектриса ОD является высотой, то есть DО 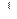 АВ.
3) Так как D АВ.
3) Так как D 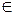 ОМ, то АВ ОМ, то АВ 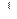 ОМ. ОМ.
|
№ 675.
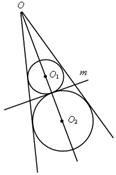
| Решение
1) Так как отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности, то точки О1 и О2 лежат на биссектрисе угла (следствие из теоремы п. 69), и, значит, точки О, О1 и О2 лежат на одной прямой.
2) О1А  m и О2А m и О2А 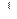 m (свойство касательной), следовательно, точки А, О1 и О2 лежат на одной прямой. Таким образом, точки А, О, О1, О2 лежат на одной прямой. Тогда точки О1 и О2 лежат на прямой ОА. m (свойство касательной), следовательно, точки А, О1 и О2 лежат на одной прямой. Таким образом, точки А, О, О1, О2 лежат на одной прямой. Тогда точки О1 и О2 лежат на прямой ОА.
|
№ 676 (а).
Решение
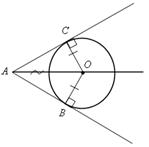
| 1)  АОВ = АОВ =  АОС (по гипотенузе и катету), тогда АОС (по гипотенузе и катету), тогда  ОАВ = ОАВ = 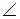 ОАС = ОАС =  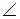 BAC.
2) BAC.
2)  АОВ, АОВ, 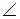 В = 90°
sin В = 90°
sin 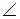 ОАВ = ОАВ = 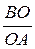 ,
ВО = ОА · sin ,
ВО = ОА · sin 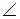 ОАВ = = ОА · sin ОАВ = = ОА · sin 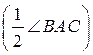 , ,
|
ОА = 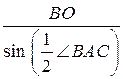 ; ОА =
; ОА = 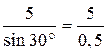 = 10 (см).
= 10 (см).
| IV. Итоги урока . OK = ON = OM. | 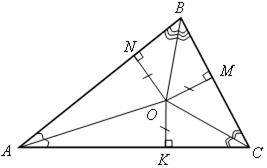
|
Домашнее задание: вопросы 15, 16, с. 187; №№ 676 (б), 778 (а).
Урок 57
Серединный перпендикуляр к отрезку
|
|
|
Цели: ввести понятие серединного перпендикуляра к отрезку; рассмотреть теорему о серединном перпендикуляре и следствие из него.
Ход урока
I. Проверка домашнего задания.
1. № 778 (а) вынести решение на доску.
2. Решить устно:

| 1) Найти: SАВЕ. |

| 2) ВМ = m, 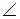 АВС = α.
Найти расстояние от точки М до прямой АС. АВС = α.
Найти расстояние от точки М до прямой АС.
|
II. Изучение нового материала.
1. Прямая KМ перпендикулярна к стороне АВ треугольника АВС и делит ее пополам. Точка М лежит на стороне АС. Докажите, что АС > ВС.
2. Ввести понятие серединного перпендикуляра к отрезку.
3. Доказать теорему о свойстве серединного перпендикуляра.
4. Доказать следствие из этой теоремы.
5. Теорема о точке пересечения высот треугольника
III. Закрепление изученного материала.
Решить №№ 679 (б), 680, 682.
2. Решить №№ 677, 684, 687.
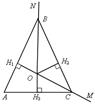
№ 677.
Решение
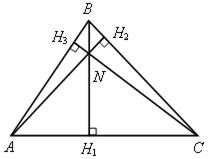
1) 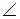 АВО = 180° – АВО = 180° – 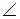 АВN = 180° – – АВN = 180° – – 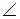 СВN = СВN = 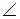 CВО, то есть ВО – биссектриса CВО, то есть ВО – биссектриса 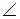 АВС, аналогично СО – биссектриса АВС, аналогично СО – биссектриса 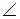 АСВ.
2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ, ВС, АС. Таким образом, ОН1 = ОН2 = ОН3, где ОН1 АСВ.
2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ, ВС, АС. Таким образом, ОН1 = ОН2 = ОН3, где ОН1 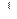 АВ, ОН2 АВ, ОН2 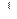 ВС, ОН3 ВС, ОН3 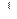 АС. АС.
| 
|
2. Получили, что АВ, ВС, АС – касательные к окружности с центром в точке О и радиусом, равным ОН1.
|
|
|
№ 684.
Решение
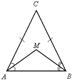
| 1) По свойству углов при основании равнобедренного треугольника
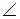 САВ = ÐСВА.
Тогда САВ = ÐСВА.
Тогда  МАС = МАС = 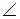 МАВ = МАВ =  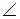 САВ =
= САВ =
=  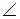 СВА = СВА = 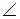 МВС = МВС =  МВА. МВА.
|
2)  МАВ – равнобедренный, АМ = ВМ и точка М лежит на серединном перпендикуляре к АВ.
МАВ – равнобедренный, АМ = ВМ и точка М лежит на серединном перпендикуляре к АВ.
3) Так как АС = СВ, то точка С также лежит на серединном перпендикуляре к АВ. Таким образом, СМ  АВ.
АВ.
№ 687.
Решение
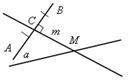
| 1) построим серединный перпендикуляр m к отрезку АВ. 2) Точка М – точка пересечения m c а. 3) М – искомая. |
Задача имеет решение в случае, если прямая АВ не перпендикулярна к данной прямой а.
Итоги урока
Четыре замечательные точки треугольника.
|
| 1) О – точка пересечения медиан треугольника АВС. АМ : МА1 = ВМ = МВ1 = СМ =
| |
| 2) K – точка пересечения серединных перпендикуляров к сторонам треугольника АВС. АK = KС = KВ.
| ||
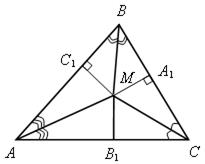
| 3) М – точка пересечения биссектрис углов треугольника АВС. МС1 = МА1 = МВ1.
| |
| 4) N – точка пересечения высот треугольника (или их продолжений). | ||
Домашнее задание: вопросы 17–19, с. 187–188; №№ 679 (а), 681, 688, 720.
Урок 57
ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ
ТРЕУГОЛЬНИКА
Цели : рассмотреть теорему о точке пересечения высот треугольника.
|
|
|
Ход урока
Дата добавления: 2018-09-20; просмотров: 545; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!