Влияние изменения внешних условий на равновесия.

⇐ ПредыдущаяСтр 4 из 13Следующая ⇒

Влияние изменения температуры на термодинамические равновесия в общем виде было впервые установлено А. Л. Потылицыным (1880). Через несколько лет это влияние было выражено Вант-Гоффом (1883) в количественной форме. Немного позже Ле-Шателье (1885), а затем Браун (1886) сформулировали общий принцип, отражающий влияние изменения различных факторов на положение равновесия, — принцип смещения равновесий, называемый иначе принципом Ле-Шателье, который можно выразить следующим образом.

Если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя какое-нибудь из условий, определяющих положение равновесия, то в системе усилится то из направлений процесса, течение которого ослабляет влияние произведенного воздействия, и положение равновесия сместится в том же направлении.

Учитывая, что истинное равновесие всегда отвечает равенству скоростей прямого и обратного процессов, можно сказать, что смещение равновесия происходит в том случае, когда произведенное воздействие неодинаково влияет на скорости прямого и обратного процессов. Это нарушение равенства скоростей и приводит к смещению равновесия и переходу системы в новое состояние равновесия, при котором скорости прямой и обратной реакций опять станут одинаковыми между собой, но будут отличаться от первоначальных.

Рассмотрим влияние изменения только двух важнейших факторов, определяющих положение равновесия,—температуры и давления.

Возьмем для примера простейшую систему, состоящую из компонентов А, В и С. В результате реакции А и В образуется С.

А + В ↔ С

Рассмотрим сначала влияние изменения температуры. Как будет смещаться равновесие в этой системе при повышении температуры? Реакция образования С из компонентов А и В сопровождается выделением теплоты (экзотермическая реакция). При обратной же реакции теплота поглощается (эндотермическая реакция). Повысить температуру системы, находящейся в равновесии, можно только, подводя к ней теплоту извне. Такое воздействие вызовет усиление того из направлений реакции, которое сопровождается поглощением теплоты, т. е. диссоциацию С. Это смещение равновесия ослабит влияние оказанного внешнего воздействия.

В общей форме влияние изменения температуры можно выразить таким образом:

повышение температуры всегда благоприятствует накоплению тех веществ, которые образуются в данной реакции с поглощением теплоты, т. е. усиливает эндотермическое направление процесса. Понижение температуры действует в противоположном направлении.

Чем большим тепловым эффектом обладает данный процесс, тем сильнее смещается равновесие с изменением температуры. В процессах же, в которых тепловой эффект мал, равновесие при изменении температуры смещается незначительно.

Рассмотрим влияние изменения давления для процесса кипения воды, выяснив, как будет смещаться равновесие при повышении или понижении давления (фиг.6,7).

Повышение давления от Р₁ до Р₂ усилит то из направлений процесса, которое сопровождается уменьшением объема, и это ослабит влияние произведенного воздействия, то есть произойдет конденсация части воды, за счет чего объем жидкости (V_ж2) несколько увеличится, а объем пара (V_п2) значительно уменьшится. Понижение давления от Р₁ до Р₃ приведет к уменьшению объема жидкости до V_ж3 и увеличению объема пара V_п3. Общий объем V₀ в первом случае уменьшится до V₁, а во втором увеличится до V₂. На кривой равновесия (фиг.7) эти состояния будут отображены соответственно точками Р₁, Р₂ и Р₃.

В общей же форме влияние изменения давления на положение равновесия можно выразить следующим образом: повышение давления благоприятствует образованию фаз, занимающих в данных условиях меньший объем, т. е. усиливает то из направлений процесса, которое сопровождается уменьшением объема. Понижение давления действует в противоположном направлении.

Чувствительность положения равновесия к изменениям давления оказывается тем большей, чем большим изменением объема сопровождается данный процесс. В процессах же, в которых изменение объема незначительно, равновесие слабо смещается при изменении давления.

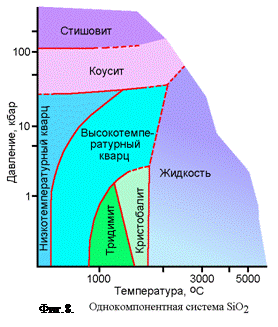
Значительные изменения объема могут происходить только в реакциях, в которых участвуют газы, т. е. когда хотя бы один из компонентов находится в газообразном состоянии. В процессах же, происходящих в конденсированных фазах, ни один из компонентов реакции не находится в газообразном состоянии и, следовательно, значительных изменений объема происходить не может. Принцип Ле-Шателье можно наглядно продемонстрировать фазовыми переходами SiO₂(фиг.8), когда по мере повышения давлений происходят реакции приводящие к образованию более плотных фаз, таких как коусит, стишовит.

Если мы будем повышать давление вдоль пунктирной линии N-M, то мы все время будем наблюдать увеличение плотности, а если будем двигаться вверх вдоль линии K-L, то будет происходить поглощение системой теплоты.

Принцип смещения равновесий распространяется и на другие факторы. Если равновесие в процессе зависит от внешних электрических, магнитных полей или поля тяготения, то при изменении их усиливается то из направлений процесса, которое уменьшает влияние произведенного воздействия. Точно так же влияет и введение дополнительных количеств одного из компонентов реакции, в чем можно убедиться из рассмотрения константы равновесия.

ПРАВИЛО ФАЗбыло сформулировано в 1870 г. Уиллардом Гиббсом, а позднее изучено более детально многими другими учеными. Термодинамическая основа этого правила рассматривается в большинстве учебников и книг по физической химии. Обычно правило фаз записывают в виде следующего уравнения:

Р+F=С+2,

где Р—число фаз, F—число степеней свободы и С—минимальное число компонентов.

Число компонентов С характеризует минимальное количество химических составных частей, необходимое и достаточное для описания состава всех фаз системы. Это позволяет классифицировать любую систему в соответствии с количеством присутствующих химических компонентов. Система, при различных условиях состоящая из воды, льда и водяного пара или из других комбинаций этих трех фаз, должна быть отнесена к однокомпонентным системам, ибо все фазы имеют один и тот же состав Н₂О.

Рассмотрим систему, которая в зависимости от условий содержит кварц (SiO₂), тридимит (SiO₂), кристобалит (SiO₂) и пироксен—энстатит (MgSiO₃). Здесь наблюдаются две фазы разного состава, и систему следует считать двухкомпонентной. В данном случае компонентами будут SiO₂ и MgSiO₃. Если появится добавочная фаза, такая, как оливин—форстерит (Mg₂SiO₄), система независимо от этого остается двухкомпонентной, так как все возможные фазы можно выразить через SiO₂, Mg₂SiO₄ или их смеси (т. е. SiO₂+ Mg₂SiO₄= 2MgSiO₃). Минерал периклаз (MgO) не изменяет число компонентов в системе, поскольку все фазы состоят из SiO₂, MgO или из их смесей.

Изучая систему, в которой кальцит (СаСО₃) претерпевает термическое разложение с образованием извести (СаО) и СО₂, было бы неправильным принять ее за трехкомпонентную (Са—С—О), так как все ее фазы могут быть представлены двумя компонентами СаО и СОа либо их смесями. Правило фаз определяет не природу выбранных отдельных компонентов, а минимальное их число. Для удобства графического изображения выбирают определенные очевидные комбинации.

Число степеней свободы F (вариантность) нагляднее представить на фазовой диаграмме. На фиг. 8 показана однокомпонентная система SiO₂. На вертикальной оси отложена температура в градусах, а на горизонтальной—давление в килобарах; масштаб логарифмический. Один килобар равен 1000 барам, а один бар — 0,9869 атмосферы. Каждая точка внутри системы отвечает определенным значениям давления и температуры. Кроме того, на диаграмме показаны области стабильности различных фаз SiO₂. Диаграммой пользуются для определения фазы или фаз, находящихся в равновесии, при любом давлении и температуре. При этом учитывается не только то, что SiO₂ может быть газообразным, жидким и твердым, но также способность последнего образовывать шесть различных структурных полиморфных модификаций. В точке А (1000°С и 5 кбар) устойчивой фазой является высокотемпературный кварц; в точке В одновременно сосуществуют высокотемпературный кварц и тридимит, а в точке С наблюдается ассоциация высокотемпературного кварца, тридимита и кристобалита. Число степеней свободы F можно определить как минимальное число переменных, необходимое для определения частных условий системы. Для этого иногда достаточно указать количество присутствующих фаз, но чаще необходимо знать также давление и температуру. Если создать обстановку, в которой сосуществуют три фазы — кристобалит, тридимит и высокотемпературный кварц, то, как видно на диаграмме, эта ассоциация будет отвечать положению только одной точки С. Сосуществование этих трех фаз наблюдается при определенных давлении и температуре, которые отвечают положению точки на диаграмме. Так как условия равновесия системы исключают произвольное изменение давления и температуры, число степеней свободы равно нулю. Это вытекает из правила фаз путем ряда соответствующих подстановок:

Р + F = С + 2,

3+F= 1+2,

F = 0.

Случай, когда в однокомпонентной системе при трех сосуществующих фазах F=0, соответствует инвариантному состоянию системы. Точка С является инвариантной. Ни давление, ни температура не могут измениться (степени свободы отсутствуют) без того, чтобы одна или две фазы не исчезли. В точке В сосуществуют тридимит и высокотемпературный кварц, однако температура и давление такой ассоциации не однозначны, поскольку возможно изменение их комбинаций (вдоль линии CBD), при которых будут образовываться обе эти фазы. Для понимания состояния конкретной системы необходимо уметь определять давление и температуру ассоциации фаз. Сделать это можно, задавая один из параметров двухфазной ассоциации: либо температуру, либо давление. Если при 1000° С стабильно сосуществуют тридимит и высокотемпературный кварц, то. исходя из диаграммы, давление в системе будет несколько меньше 1 кбар. Таким образом, имеются одна зависимая и одна независимая переменные. Другими словами, одна независимая переменная определяет состояние, при котором возможна „одна степень свободы или одна „степень вариантности. Поэтому линии, характеризующие такие системы, называют моновариантными кривыми. Это условие легко вывести из правила фаз, произведя соответствующие подстановки:

Р + F =С+2,

2 + F=1+2,

F = 1.

На диаграмме все переходные кривые являются моновариантными и каждая из них обладает одной степенью свободы.

Для полного определения состояния системы недостаточно указания, что в ней существует только одна высокотемпературная модификация кварца (как, например, в точке А). Высокотемпературный кварц может существовать при различных комбинациях температуры и давления. Поле существования высокотемпературной модификации кварца, как и других единичных фаз, является дивариантной областью. Правило фаз указывает на наличие двух степеней свободы.

Правило фаз позволяет не только классифицировать системы, но и помогает при интерпретации диаграмм. Так, рассматривая диаграмму системы SiO₂ (фиг. 8), легко заметить, что в ней нет какой-либо области или точки, где одновременно находилось бы более трех фаз. Если предположить, что в системе имеется четырехфазная ассоциация, то правило фаз указывает на ее нестабильность, так как степень свободы оказывается отрицательной:

P+F=С+2,

4+F=1+2,

F= -1.

Поскольку F характеризует минимальное число переменных, фиксирующих состояние системы, оно должно быть либо положительным, либо равным нулю. При F=0 в системе будет наблюдаться максимальное количество стабильно сосуществующих фаз. Такой подход применим и к многокомпонентным системам; например, в 20-компонентной системе максимальное число стабильно сосуществующих фаз равно 22. Если же присутствуют дополнительные фазы, система неравновесна. Этот критерий был использован при изучении петрологии метаморфических процессов для определения равновесности частных минеральных .ассоциаций. В случае когда число присутствующих фаз превышает то, которое диктуется правилом фаз, неравновесие считается доказанным, однако обратное не обязательно. Хотя число присутствующих фаз может находиться в соответствии с условиями равновесия, вполне возможно, что некоторые фазы в установленных условиях нестабильны. Приложение правила фаз к метаморфическим ассоциациям часто затруднено из-за недостатка точных сведений о числе присутствующих компонентов.

Классифицировать системы наиболее удобно в зависимости от числа компонентов. Исходя из правила фаз и числа присутствующих фаз, можно определить число степеней свободы любой ассоциации фаз. В присутствии дивариантной ассоциации фаз (например, в поле первичной кристаллизации высокотемпературного кварца, фиг. 8) изменяются две переменные—давление и температура (или концентрация в системах, содержащих более одного компонента); эти изменения могут происходить независимо друг от друга. Фазовая ассоциация, отвечающая моновариантным условиям (кривая CBD, фиг. 8), сохраняется, если изменение одной переменной сопровождается соответствующим изменением второй. Инвариантная ассоциация (точка С, фиг. 8) может существовать только в том случае, если не происходит изменение температуры, давления, состава или любой другой переменной. В задачу исследователя-экспериментатора входит определение инвариантных и моновариантных условий.

Следует всегда помнить, что, хотя многие экспериментально установленные реакции удовлетворяют требованиям правила фаз, они могут не отражать равновесных процессов, происходящих в действительности. Тот факт, что исследователю неоднократно удается синтезировать какую-либо фазу при определенных параметрах давления и температуры, еще не говорит о том, что эта фаза является самой стабильной при данных условиях. Это может просто означать, что эта фаза более устойчива, чем исходный материал. При условии достаточного времени минерал перейдет в еще более стабильную форму. Проблема метастабильных реакций особенно важна для относительно низкотемпературных гидротермальных процессов. В дискуссии по определению равновесия в экспериментальных системах Файфом сделано следующее заключение: «В том случае, когда результаты эксперимента противоречат выводам, основанным на геологических наблюдениях, исследователь обязан особо внимательно проверить представительность и совершенство своей лабораторной методики». В то же время каждый полевой исследователь, применяя экспериментальные данные при решении геологических проблем, должен иметь в виду их возможные недостатки.

ОДНОКОМПОНЕНТНЫЕ и БИНАРНЫЕ СИСТЕМЫ

Однокомпонентные системы

Одним из наиболее общих правил при работе с диаграммами давление—температура, является то, что давление в системе вызывает уменьшение объема, а температура (в общем случае) —увеличение его. Таким образом, давление и температура по своему действию противоположны друг другу. Специфика изменений объема системы в зависимости от температуры и давления бывает различной, однако основной принцип сохраняется.

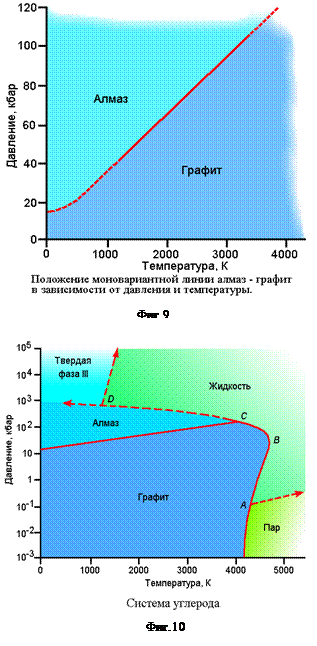
Наиболее изученной однокомпонентной системой является система углерода. Первоначальные попытки синтезировать алмаз были описаны в 1955 г. Банди и др. , а кривая равновесия алмаз—графит (фиг. 9) опубликована в 1961 г. Как видно из диаграммы, высокое давление способствует стабильности более плотной полиморфной модификации—алмаза (мол. объем = 3,42 см3/моль), тогда как при высоких температурах стабильна менее плотная модификация—графит (мол. объем = 5,33 см3/моль). В 1962 г. при исследовании высокотемпературной области системы углерода Банди определил положение кривой плавления для графита и алмаза (фиг. 10). Кривая графит—жидкость между точками А и В показывает, что увеличение давления на жидкость при фиксированной температуре приводит к образованию графита, что говорит о большей плотности графита по сравнению с жидкостью. При более высоких давлениях (между точками В и С) кривая имеет противоположный наклон, т. е. дальнейшее увеличение давления вызывает переход графита в жидкость большей плотности. Кривая алмаз—жидкость между точками С и D также имеет отрицательный наклон, указывающий на то, что увеличение давления заставляет плотный алмаз переходить в еще более плотную жидкость. По аналогии с другими системами было высказано предположение о существовании твердой фазы (фаза III) при давлениях более высоких, чем требуется для стабильности алмаза. Как известно, алмаз не стабилен при обычных параметрах давления и температуры. Однако он существует метастабильно, подобно полиморфным модификациям других соединений, устойчивым при высоких давлениях. Еще в 1900-х годах Бриджмен провел большое количество исследований при высоких давлениях, в частности им была детально изучена система H2O при низких температурах. Современные знания об этой системе отражает фиг. 11. Помимо обычного льда (лед I), установлено существование пяти его полиморфных модификаций. Так как лед I имеет меньшую плотность, чем вода, его температура плавления уменьшаетсяс увеличением давления. Отрицательным наклоном кривой плавления часто объясненяется подвижность масс глетчерного льда. В основании толстого глетчера точка плавления льда может существенно понизиться, и вызванное этим плавление приведет в движение всю замороженную массу. Как можно видеть на фиг. 11, лед I при температуре, соответствующей точке А, плавится, когда давление возрастает до точки В. При дальнейшем увеличении давления жидкость в точке С будет замерзать с образованием льда III. При еще большем давлении в точке D наблюдается инверсия льда III в лед V; в точке Е, лед V переходит в лед VI, который в точке F превращается в лед VII.

Общие закономерности изменения объемов для диаграмм подобного типа можно вывести на основании уравнения Клапейрона, которое характеризует наклон кривой в координатах температура — давление:

dT/dP=TDV/DH

где dT/dP — скорость изменения температуры перехода в зависимости от давления, Т—температура, для которой рассчитана кривая перехода, DH — теплота перехода, a DV—разница в объемах высоко- и низкотемпературной фаз. Разность объемов может представлять собой V_газ - V_жидк., V_жидк. - V_{тв. ф.}и V_тв.ф.I- V_{тв. ф.II}. Наиболее эффективно это уравнение для перехода газ — жидкость, но оно также применимо для переходов жидкость—твердая фаза и твердая фаза—твердая фаза. Из-за уменьшения DV с увеличением давления (так же, как с изменением DH) для большинства кривых перехода наблюдается уменьшение наклона (dT/dP) с увеличением давления. При нормальных распределениях плотностей между фазами низкотемпературная фаза имеет меньший объем и положительную величину DV, так как объем высокотемпературной фазы больше объема низкотемпературной фазы; наклон кривой перехода также положительный. В общем виде взаимоотношения плотностей суммированы на фиг. 12. Если не наблюдается никакого изменения объемов высоко- и низкотемпературной фаз, наклон отсутствует и изменение давления не влияет на переход. Если высокотемпературная фаза более плотная, как при переходе льда I в воду, кривая будет иметь отрицательный наклон.

Относительные плотности различных фаз в системе H₂O легко установить, исходя из диаграммы (фиг. 11). Наблюдаемая последовательность фаз с возрастанием давления от точек А и G показана ниже:

(точка А) лед I ® вода ® лед III ® лед V ® лед VI ® лед VII, (точка G) лед 1 ® лед III ® лед II ® лед V ® лед VI ® лед VII. Суммируя данные этих двух рядов, можно получить порядок возрастания плотностей фаз: лед I, вода, лед III, лед II, лед V, лед VI и лед VII.

На фиг. 13 приводится диаграмма давление — температура системы SiО₂. Наклон кривых полиморфных переходов говорит о том, что плотности кристобалита, тридимита и жидкости почти равны, тогда как наибольший рост плотности, очевидно, наблюдается при переходе высоко- и низкотемпературного кварца в коусит и коусита в стишовит. При давлении около 1 кбар кристобалит и тридимит, обладающие низкими плотностями, переходят в кварц. Очень плотные коусит и стишовит наблюдаются только в условиях ударных или взрывных процессов.

Бинарные системы

Двухкомпонентные, бинарные, системы при атмосферном давлении. Для таких систем правило фаз (обычно записывамое P+F=C+2) нужно преобразовать следующим образом: P+F=C+1, так как давление в этом случае не изменяется. В такой форме оно называется правилом фаз для конденсированных систем, поскольку газовой фазой, присутствующей в ничтожно малом количестве, можно пренебречь, считая ее сконденсированной до жидкого состояния.

Простейшие равновесные взаимоотношения показаны на примере двухкомпонентной системы CaAl2Si₂O₈ (анортит) и CaSiTiO₅ (сфен), изображенной на фиг. 14. Ось абсцисс на этой фигуре отражает состав от чистого CaSiTiO₅ слева до чистого CaAl2Si₂O₈ справа. Содержание компонента CaAl2Si₂O₈ в процентах увеличивается слева направо, как показано цифрами на шкале. Процентное содержание другого компонента увеличивается справа налево. Для большинства фазовых диаграмм содержание компонентов приводится в массовых процентах; лишь в некоторых случаях они даются в молекулярных процентах. На оси ординат отложена температура в градусах Цельсия; однако на тех диаграммах, которые изучены в странах английского языка с целью использования их в керамической промышленности, температура может быть приведена в градусах Фаренгейта.

Любой точке в пределах диаграммы отвечают определенные параметры состава и температуры. Сплошными линиями на диаграмме ограничены области или поля температур и составов, в пределах которых показаны равновесные ассоциации фаз. Так как мы здесь рассматриваем только конденсированные системы, эти области содержат ассоциации четырех типов — жидкость, жидкость + твердые фазы, твердые фазы и реже жидкость + жидкость. В зависимости от сложности системы фазовая диаграмма характеризуется различным числом таких областей. Фазовые диаграммы строятся на основании данных, полученных при нагревании различных смесей минералов, химических реагентов или стекол до определенных температур, и изучения фазовых ассоциаций, возникающих при этих температурах. При изучении силикатных систем обычно пользуются быстрым охлаждением (закаливанием) нагретых образцов с тем, чтобы сохранить высокотемпературные ассоциации при низкой температуре в метастабильном состоянии.

На фиг. 14 видно, что различные поля диаграммы содержат одну или две фазы: жидкость, жидкость + сфен, жидкость + анортит, а также сфен + анортит. Любая точка, располагающаяся в пределах однофазного поля, отвечает единственной фазе, состав которой строго определяется ее проекцией на ось абсцисс. Положение точки А на диаграмме соответствует жидкой фазе, имеющей состав 80 мас. % CaAl2Si₂O₈ и 20 мас. % CaSiTiO₅. Точка В, характеризующая систему с тем же валовым составом, но находящуюся при более низкой температуре, попадает в двухфазную область; составы этих двух фаз устанавливаются с помощью горизонтальной линии, проведенной через рассматриваемую точку к границам области—в данном случае к точкам С и D. Такая линия, называемая соединительной линией, или реже конодой, указывает на составы находящихся в равновесии двух фаз. Состав жидкой фазы, определяющийся положением точки С, отвечает 57 мас. % CaAl₂Si₂O₈ и 43 мас. % CaSiTiO₅. Состав твердой фазы, характеризующийся точкой D, соответствует чистому анортиту CaAl₂Si₂O₈. Если шихту этого же состава охлаждать до точки Е в пределах двухфазной области сфена и анортита, она будет состоять из этих кристаллических фаз, причем их составы отражают точки F и G на крайних левой и правой сторонах диаграммы.

Соединительная линия указывает не только на индивидуальные составы минералов, сосуществующих в любой точке в пределах двухфазного поля, но также определяет относительные количества каждого из них при равновесных условиях. Рассмотрим вновь соединительную линию, которая проходит через жидкость состава С, и сосуществующий с ней анортит D. Видно, что если валовой состав системы (точка В) ближе к составу одной из двух фаз, то эта фаза преобладает. Если же валовой состав системы попадает точно на середину между составами этих двух фаз, они присутствуют в равных количествах. Можно, следовательно, измерив расстояние от точки валового состава системы до точек составов каждой фазы, определить относительные их количества. В данном случае длина отрезка СВ соответствует относительному количеству анортита, a BD — количеству жидкой фазы, причем длина CD принимается за сумму. Другими словами, мы можем сказать, что

BC/CD*(100)=2,25 см /4,15 см *(100)=54.2% анортита

BD/CD*(100)=1,.90 см /4,15 см *(100)= 45,8% жидкости

Это—простое, но чрезвычайно полезное отношение, называемое правилом рычага (Или принципом центра тяжести) .

На фиг. 14 видно, что температура плавления сфена 1382°С, а анортита 1550°С. Расплавы чистых сфена или анортита полностью застывают, а кристаллы плавятся при указанных температурах. Жидкости, образующиеся при плавлении этих двух минералов, полностью смешиваются, что показано на диаграмме единой непрерывной областью существования расплава. Система промежуточного состава характеризуется сложным поведением при застывании или плавлении. Состав расплава, обозначенного на фиг. 14 точкой А, отвечает 80% компонента CaAI₂Si₂O₈ и 20% компонента CaSiTiO₅. Хотя этот расплав состоит главным образом из CaAI₂Si₂O₈, он застывает не при 1550°С, как чистый анортит. Примесь CaSiTiO₅ снижает точку его кристаллизации до 1490 °С (точка Н). Из диаграммы видно, что при температуре несколько ниже 1490 °С появляется поле жидкость + анортит. Следовательно, кристаллизация начинается с выделения кристаллов анортита. Так как в процессе кристаллизации анортита компонент CaAl₂Si₂O₈ удаляется из расплава, остающаяся жидкость становится богаче CaSiTiO₅; состав ее смещается по направлению к левой стороне диаграммы, и точка кристаллизации соответственно снижается. Эти изменения в составе и температуре застывания остаточного расплава отражает линия HCI, которая графически показывает, что происходит с жидкой фазой при потере системой тепла и кристаллизации анортита. Используя правило фаз, можно определить составы фаз и относительные их пропорции для всех температур в двухфазной области.

Непрерывное удаление тепла и выделение анортита в конечном счете приводят состав жидкой фазы к точке I, которая является точкой минимальной температуры поля жидкости, или эвтектической точкой. Ниже температуры эвтектики жидкость присутствовать не может. Горизонтальная линия, проведенная через точку I, называется солидусом; она определяет верхнюю границу полей, содержащих только твердые фазы. Две наклонные кривые, характеризующие нижние пределы однофазного. поля жидкости, называются ликвидусными линиями.

В эвтектической точке из остаточного расплава начинают одновременно кристаллизоваться две фазы. Относительные количества этих фаз определяются путем измерения плеч рычага на соединительной линии, проведенной через точку I; в данном случае анортит составляет 37%, а сфен—63%. Так как соотношение этих двух фаз при кристаллизации остается постоянным, состав жидкой фазы также не изменяется. До тех пор пока не будет использована последняя порция жидкости, температура системы тоже остается постоянной. После этого удаление тепла' приводит к падению температуры. Независимо от степени дальнейшего охлаждения системы сфен и анортит продолжают существовать в устойчивом равновесии. Как следует из измерения длин плеч рычага на соединительной линии FEG, конечная фазовая ассоциация будет содержать 80% анортита и 20% сфена; она представляет собой сумму твердых фаз, образовавшихся при кристаллизации эвтектического расплава с постоянным соотношением компонентов, и твердых фаз, выделившихся ранее, выше температуры эвтектики (в данном случае в температурном интервале HI). Конечная кристаллическая смесь соответствует эвтектическим пропорциям только тогда, когда исходный состав расплава отвечает эвтектическому.

Относительные количества двух сосуществующих фаз можно легко определить с помощью правила рычага (как было сделано для точек В и E). Для реакций, происходящих в инвариантных точках (таких, как I), где сосуществуют три фазы, нельзя установить процентные, соотношения фаз, пользуясь правилом рычага, поскольку они зависят от удаленного из системы тепла. Однако начальные и конечные пропорции фаз таких реакций определить можно.

Историю кристаллизации жидкости состава А можно представить себе, наблюдая за изменением скорости охлаждения ее в процессе эксперимента. Предположим, что расплав (фиг. 14) охлаждается естественным образом. При этом падение температуры в нем регистрируется температурно-чувствительным прибором, таким, как термопара, на непрерывно движущейся диаграммной ленте. График в координатах температура - время, отражающий историю охлаждения, будет напоминать показанный на фиг. 15. Первоначально расплав охлаждается быстро. Когда начинает кристаллизоваться анортит (в точке H), скорость охлаждения замедляется благодаря теплоте кристаллизации. При охлаждении расплава до температуры эвтектики в точке I сфен и анортит начинают кристаллизоваться совместно, и температура остается постоянной до тех пор, пока не будет израсходована вся жидкость (по правилу фаз для конденсированных систем; P+F=C+1; 3+F=2+1; F=0). После завершения процесса кристаллизации система вновь охлаждается с большой скоростью.

Расплав любого произвольного состава будет кристаллизоваться по той же самой схеме, что была показана на примере расплава состава А. Например, кристаллизация расплава состава J (фиг. 14) при охлаждении до точки К. на линии ликвидуса начинается с образования сфена. При дальнейшей потере тепла образуется дополнительное количество сфена, а остающаяся жидкость обогащается CaAI₂Si₂O₈. Состав жидкости изменяется согласно положению ликвидуса до тех пор, пока система не охладится до точки I, отвечающей температуре эвтектики. Здесь сфен и анортит кристаллизуются совместно при постоянной температуре и в фиксированном соотношении до полного исчезновения расплава.

Жидкость, состав которой отвечает эвтектическому, охлаждаясь до температуры эвтектики, целиком кристаллизуется при постоянной температуре, что подтверждается и правилом фаз для конденсированных систем; трехфазная ассоциация не имеет степеней свободы и, следовательно, является инвариантной. Температура и составы фаз трехфазной ассоциации должны оставаться постоянными до тех пор, пока не будет исключен, по крайней мере, одна из фаз.

Плавление в системе CaSiTiO₅—CaAl₂Si₂O₈ (фиг. 14) протекает прямо противоположным образом. Предположим, что твердая фаза представляет собой тонкую механическую смесь сфена и анортита; при этом оба минерала начинают плавиться одновременно при достижении системой температуры эвтектики; жидкость будет иметь эвтектический состав. В результате дальнейшего нагрева одна из твердых фаз исчезает, а состав и температура расплава начнут изменяться в соответствии с положением линии ликвидуса (в зависимости оттого, будет ли находиться в избытке сфен или анортит) до полного плавления всех кристаллов.

Очень быстрое охлаждение (закалка) приводит к метастабильному сохранению фазовых ассоциаций, равновесных при высоких температурах. Так, расплав A (фиг. 14) при закалке затвердевает в виде стекловатой массы. Подобным же образом из смеси анортита и расплава (точка В) при быстром охлаждении можно получить сплав, представляющий собой кристаллы анортита в стекловатой основной массе.

Удаление кристаллов из остывающего расплава, представляющего собой простую бинарную систему, не оказывает никакого влияния на ход кристаллизации; охлаждение его продолжается с изменением состава в соответствии с ликвидусом до тех пор, пока не будет достигнута температура эвтектики. Причина этого состоит в том, что кристаллы, будучи однажды образованы, химически не реагируют с остаточной жидкостью. Однако в ряде систем такая реакция жидкость— кристалл может иметь место, и присутствие кристаллов в расплаве или их удаление будет сильно влиять на ход кристаллизации.

Неравновесия, возникающие в результате быстрого охлаждения в подобных системах, подробно обсуждаются в работах Бакли и Тернера и Ферхугена. Путь, приводящий к образованию слоистых изверженных пород при переохлаждении, описан Таубенеком и Полдерваартом.

Дата добавления: 2018-08-06; просмотров: 658; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!